3.7整式的相除课件(17张ppt)
图片预览




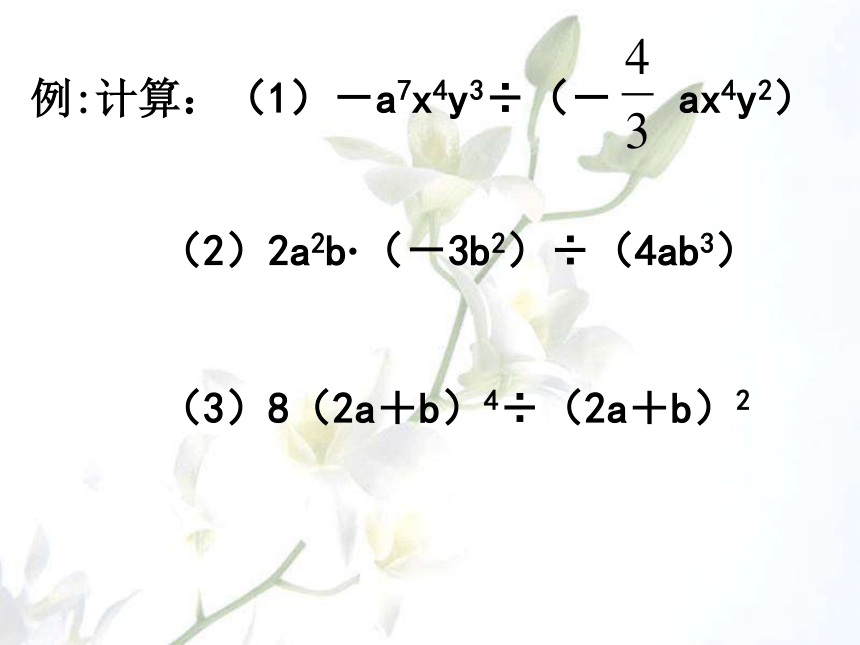

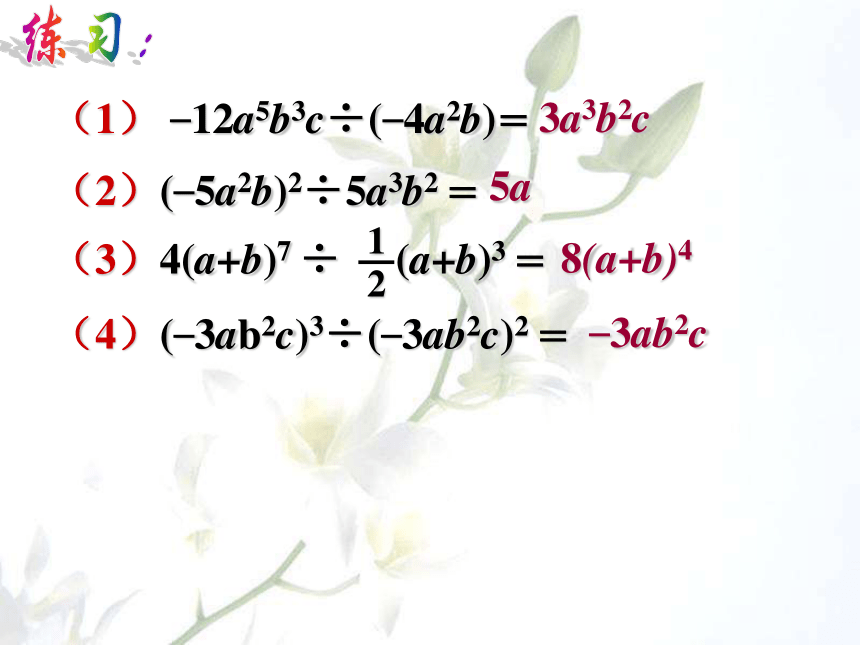
文档简介
(共18张PPT)
同底数幂的乘法
幂的乘方
积的乘方
同底数幂的除法
零指数幂性质
负整数指数幂性质
合并同类项
1、幂的运算——基础公式
单项式与单项式相乘
单项式与多项式相乘
多项式与多项式相乘
2、整式的乘法运算
(-a2c)(3ab2c3)
2x2(-x2+2x+1)
(-2m+1)(m-2)
3、多项式的乘法公式
平方差公式:
两项:(a+b)(a-b)=a2-b2
完全平方公式:
两项:(a+b)2=a2+2ab+b2
两项:(a-b)2=a2-2ab+b2
(a+b-c)2=a2+b2+c2+2ab-2ac-2bc
2.如何计算(14a3b2x5)÷(4ab2)
1.如何计算:6a3b4÷3a2b
相除
相除
不变
例:计算:(1)-a7x4y3÷(- ax4y2)
(2)2a2b·(-3b2)÷(4ab3)
(3)8(2a+b)4÷(2a+b)2
1、辨一辨:
(1)(12a3b3c)÷(6ab2)=2ab
(2)(p5q4)÷(2p3q)=2p2q3
2、练一练:计算与填空
①(10ab3)÷(5b2)=
②3a2÷(6a6)·(-2a4)=
③( )·3ab2=-9ab5
④(-12a3bc)÷( )=4a2b
3a3b2c
5a
8(a+b)4
–3ab2c
巩固与练习
底数不变,
指数相减.
保留在商里
作为因式.
(1)(-x2y3)÷(3x2y);
(2)(10a4b3c2)÷(5a3bc);
(3)(2x2y)3· (-7xy2)÷(14x4y3);
(4)(2a+b)4÷(2a+b)2.
(1)-a5x3y÷(-4ax2y)
(2)2a2b(-3b2c3) ÷4a3b2
(3)7a8b3c6 ÷(2a3b2)2.(-4a2bc)3
月球距离地球大约3.48×105千米,一架飞机的速度约为8 ×102千米/小时。如果乘坐此飞机飞行这么远的距离,大约需要多少时间?
解:
(3.84×105) ÷(8 ×102)
=0.48×103
=480 (时)=20(天)
答:如果乘坐此飞机飞行这么远的距离,大约需要20天。
做一做: P89先填空,再用适当的方法验证计算的正确性。
(1)(625+125+50)÷25
=( )÷( )+( )÷( )+( )÷( )
(2)(4a+6)÷2
=( )÷( )+( )÷( )
(3)(2a2—a)÷(-2a)
=( )÷(-2a)+( )÷(-2a)
即:
(a+b+c)÷m=a÷m+b÷m+c÷m(m≠0)
多项式除以单项式,
先把这个多项式的每一项分别除以单项式,
再把所得的商相加。
(1) (14a3-7a2)÷(7a)
(2) (15x3y5-10x4y4–20x3y2)÷(-5x3y2)
(1) (15x2y-10xy2)÷(5xy)
(2) (4c3d2-6c2d3)÷(-3c2d)
(1)辨别正误:
①(am+bm+cm2)÷m=a+b+c
②(2x-4y+3)÷2=x-2y+3
(2)计算式填空
①(15x2y-10xy2)÷(5xy)
②(4c3d2-6c2d3)÷(-3c2d)
③ [3a2-( )]÷(-a)=-3a+2b
④( )·(-2y)=4x2y-6xy2
1、(-4a3b2+8ab3)÷(4ab2)
2、(5x3-2x2+6x) ÷3x
3、(2x2y3)·(-7xy2) ÷(14x4y3)
m
平方
+m
-2
输出
任意给一个非零数,
÷m
输入m
根据程序列出式子:
同底数幂的乘法
幂的乘方
积的乘方
同底数幂的除法
零指数幂性质
负整数指数幂性质
合并同类项
1、幂的运算——基础公式
单项式与单项式相乘
单项式与多项式相乘
多项式与多项式相乘
2、整式的乘法运算
(-a2c)(3ab2c3)
2x2(-x2+2x+1)
(-2m+1)(m-2)
3、多项式的乘法公式
平方差公式:
两项:(a+b)(a-b)=a2-b2
完全平方公式:
两项:(a+b)2=a2+2ab+b2
两项:(a-b)2=a2-2ab+b2
(a+b-c)2=a2+b2+c2+2ab-2ac-2bc
2.如何计算(14a3b2x5)÷(4ab2)
1.如何计算:6a3b4÷3a2b
相除
相除
不变
例:计算:(1)-a7x4y3÷(- ax4y2)
(2)2a2b·(-3b2)÷(4ab3)
(3)8(2a+b)4÷(2a+b)2
1、辨一辨:
(1)(12a3b3c)÷(6ab2)=2ab
(2)(p5q4)÷(2p3q)=2p2q3
2、练一练:计算与填空
①(10ab3)÷(5b2)=
②3a2÷(6a6)·(-2a4)=
③( )·3ab2=-9ab5
④(-12a3bc)÷( )=4a2b
3a3b2c
5a
8(a+b)4
–3ab2c
巩固与练习
底数不变,
指数相减.
保留在商里
作为因式.
(1)(-x2y3)÷(3x2y);
(2)(10a4b3c2)÷(5a3bc);
(3)(2x2y)3· (-7xy2)÷(14x4y3);
(4)(2a+b)4÷(2a+b)2.
(1)-a5x3y÷(-4ax2y)
(2)2a2b(-3b2c3) ÷4a3b2
(3)7a8b3c6 ÷(2a3b2)2.(-4a2bc)3
月球距离地球大约3.48×105千米,一架飞机的速度约为8 ×102千米/小时。如果乘坐此飞机飞行这么远的距离,大约需要多少时间?
解:
(3.84×105) ÷(8 ×102)
=0.48×103
=480 (时)=20(天)
答:如果乘坐此飞机飞行这么远的距离,大约需要20天。
做一做: P89先填空,再用适当的方法验证计算的正确性。
(1)(625+125+50)÷25
=( )÷( )+( )÷( )+( )÷( )
(2)(4a+6)÷2
=( )÷( )+( )÷( )
(3)(2a2—a)÷(-2a)
=( )÷(-2a)+( )÷(-2a)
即:
(a+b+c)÷m=a÷m+b÷m+c÷m(m≠0)
多项式除以单项式,
先把这个多项式的每一项分别除以单项式,
再把所得的商相加。
(1) (14a3-7a2)÷(7a)
(2) (15x3y5-10x4y4–20x3y2)÷(-5x3y2)
(1) (15x2y-10xy2)÷(5xy)
(2) (4c3d2-6c2d3)÷(-3c2d)
(1)辨别正误:
①(am+bm+cm2)÷m=a+b+c
②(2x-4y+3)÷2=x-2y+3
(2)计算式填空
①(15x2y-10xy2)÷(5xy)
②(4c3d2-6c2d3)÷(-3c2d)
③ [3a2-( )]÷(-a)=-3a+2b
④( )·(-2y)=4x2y-6xy2
1、(-4a3b2+8ab3)÷(4ab2)
2、(5x3-2x2+6x) ÷3x
3、(2x2y3)·(-7xy2) ÷(14x4y3)
m
平方
+m
-2
输出
任意给一个非零数,
÷m
输入m
根据程序列出式子:
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
