第一讲 从欧氏几何看球面

(共30张PPT)
我们以前学习的平面几何和立体几何统称欧几里得几何（简称欧氏几何）
欧几里得
本讲我们从欧氏几何的角度，即把平面和球面都放到三维欧氏空间中，利用已学过的立体几何知识研究平面、直线与球面的位置关系及其几何性质，主要介绍平面与球面的位置关系、直线与球面的位置关系、球幂定理以及球面的对称性．
类似平面与球面的位置关系：
相交
相离
相切
位置关系
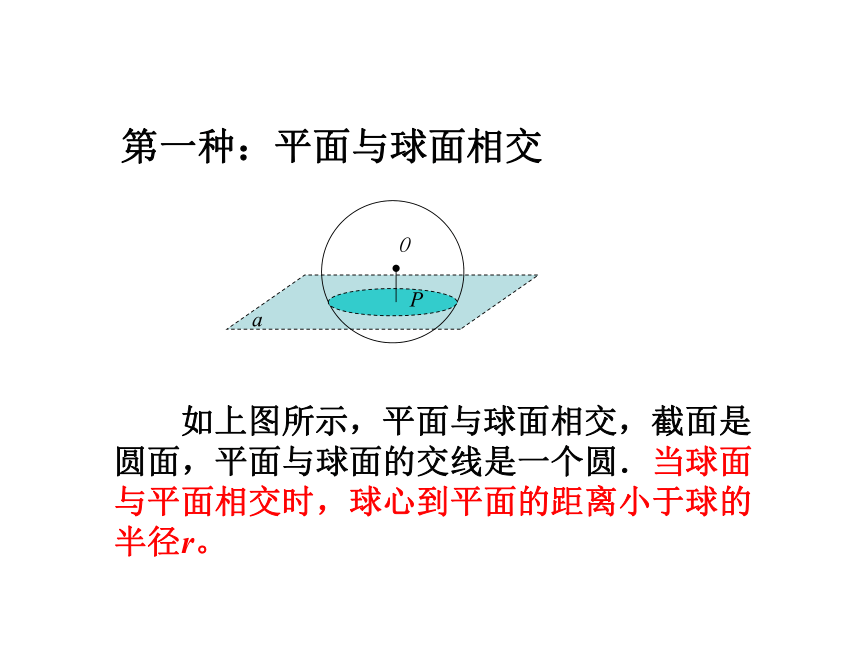
第一种：平面与球面相交
如上图所示，平面与球面相交，截面是圆面，平面与球面的交线是一个圆．当球面与平面相交时，球心到平面的距离小于球的半径r。
在平面与球面相交时，有两种情况：
1、如果球面被经过球心的平面所截，那么所截得的圆叫做大圆。
2、如果球面被不经过球心的平面所截得的圆叫小圆。
当我们把地球看作一个球时，经线就是球面上从北极到南极的半个大圆。
国际上，以过格林尼治天文台的经线为0°经线，向东叫做东经，向西叫做西经.地球球面上一点的经线的经度是过该点的经度所在的半平面与0°经线所在的半平面所成的二面角的大小．
很明显，地球表面上任意一点由经度和纬度唯一确定．
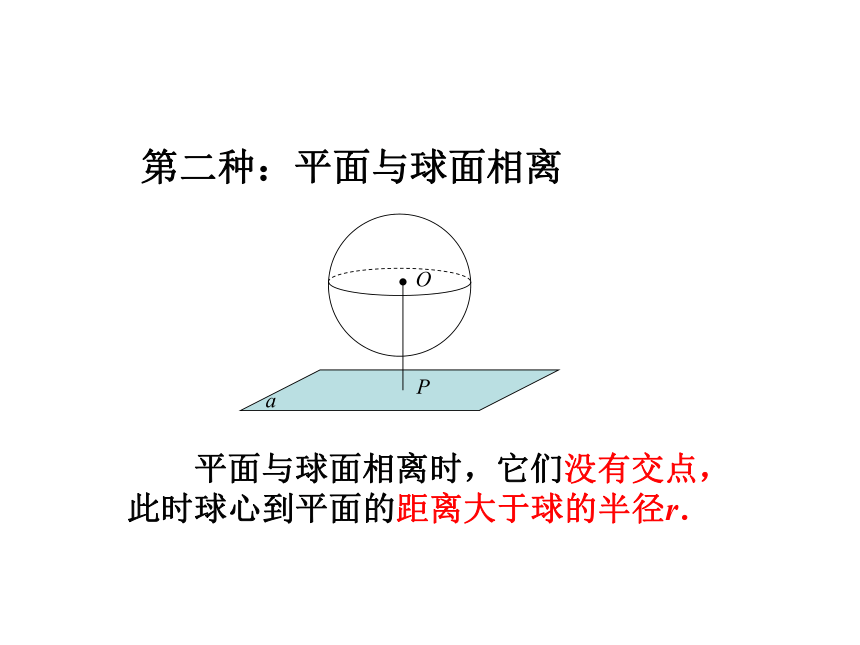
第二种：平面与球面相离
平面与球面相离时，它们没有交点，此时球心到平面的距离大于球的半径r．
第三种：平面与球面相切
平面与球面相切，有且只有一个交点，球心到平面的距离等于球的半径r．
2.1 直线与球面的位置关系
我们可以参考平面与球面的位置关系，来学习直线与球面的位置关系．因为我们可以把平面看成是由无数条直线组成．
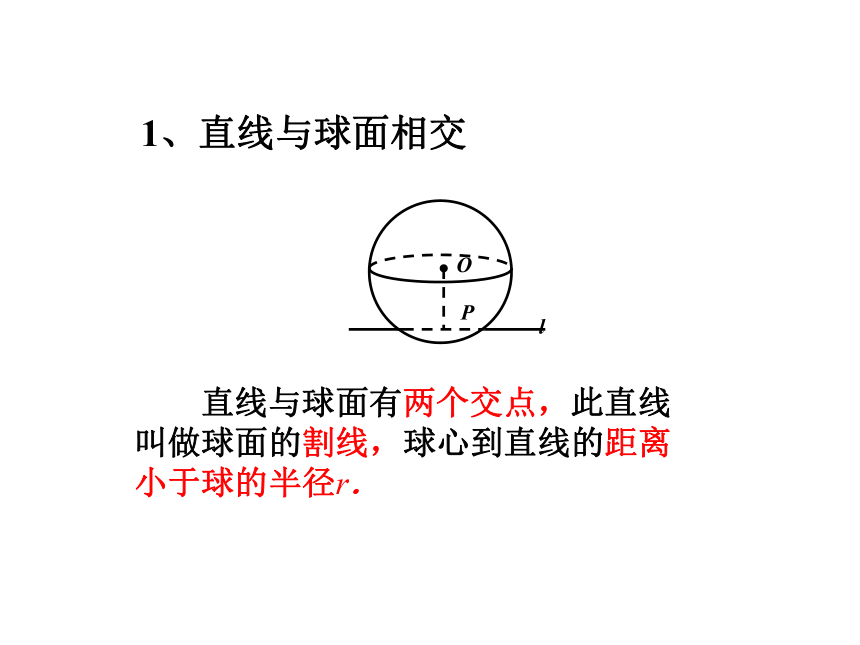
1、直线与球面相交
直线与球面有两个交点，此直线叫做球面的割线，球心到直线的距离小于球的半径r．
2、直线与球面相离
直线与球面没有公共点，球心到直线的距离大于球的半径r．
3、直线与球面相切
直线与球面有且只有一个公共点，这个公共点叫做切点，该直线叫做球面的切线，此时球心到直线的距离等于球的半径r．
过球面外一点P，引球的所有切线有什么性质？
由上图可以容易得出，过球面外一点 p 做球的切线，所有的切线（切点与 p 的距离 ）都相等，它们构成一个圆锥面．
2.2 球幂定理
观察下图，想一想我们学过的一些关于圆的定理．
之前在平面几何中学过切线长定理、切割线定理、相交弦定理，这些定理统称为圆幂定理．
类比圆幂定理，可以发现下面几个定理：
定理1 从球面外一点p向球面引割线，交球面与Q，R两点；再从点p引球面的任一切线，切点为S，则
PS 2=PQ ·PR ．
证明：如下图，连结SQ，SR．
由于两条相交直线PS，RP 唯一确定a平面，设平面a与球面的截面的圆心为O．由圆幂定理可知
PS 2=PQ · PR ．
定理2 从球面外一点p向球面引两条割线，它们分别与球面相交于Q，R，S，T四点，则
PQ·PR=PS·PT．
定理3 设 p 是球面内一点，过点 做两条直线，它们分别与球面交于Q，R，S，T四点，则
PQ·PR=PS·PT．
定理1、定理2、定理3统称为球幂定理．
你能仿照定理1的证明过程，证明定理2和定理3吗？
我们学过的圆它是对称图形，既是轴对称图形，又是中心对称图形，球面是一个旋转曲面，与圆一样，球面也有对称性．
由右图可以看出：
1、球面关于球心对称；
2、球面关于球的任意一条直 径对称；
3、球面关于球的大圆对称．
球的这种对称性有很多应用，对我们研究球面几何具有很大的帮助．
你还能发现其他一些球的对称性吗？
课堂小结
1. 平面与球面的位置关系．
相交
相离
相切
位置关系
2. 直线与球面的位置关系和球幂定理．
位置关系
相交
相离
相切
球幂定理 定理1，2，3．
3. 球面的对称性．
课堂练习
如果把地球看做一个球体，则地球上北纬60°纬线长和赤道线长的比值为（ ）
A.0.8 B.0.75
C.0.5 D.0.25
C
解析：考查有关球的问题，可知两个长度的比即为两个圆的半径比.设赤道所在圆半径为R，北纬60°所在圆的半径为r，由纬度定义可知