第二讲 球面上的距离和角

(共32张PPT)
上一讲中，运用欧式几何的方法，研究了球面的一些性质．这次课从球面上的距离和角入手，进入球面几何的学习．
欧式几何中，用距离和角度（方位）来刻画位置间的关系，对于球面的学习，从球面上的距离和角两个基本概念开始．
一、球面上的距离
我们知道，在平面上，经过两点可以连一条直线，且只可连一条直线．平面上两点之间的所有连线中，线段最短，这条线段的长度叫做两点之间的距离．
平面上的两条直线有两种位置关系：平行和相交，如果相交，那么只有一个交点．平面上的直线可以无限延长等等．这些都是平面上直线的性质．
在平面上可以画出直线，但球面是一个曲面，球面上的线是弯曲的，不存在直线．
球面上有没有某种曲线可以“扮演”平面上直线的角色呢？连结球面上任意两点有无数条曲线，而且它们的长短不一，其中是否存在一条最短的曲线？
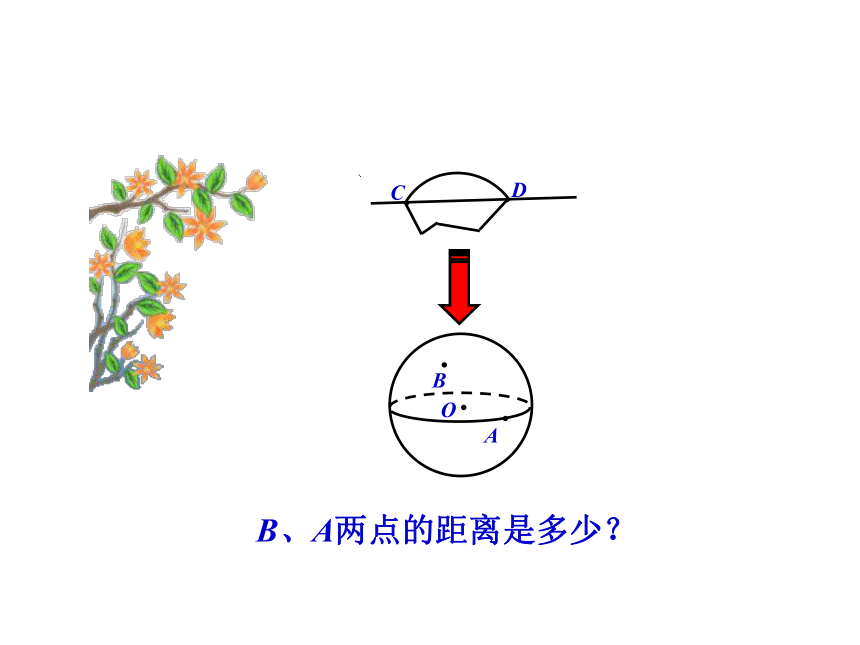
B、A两点的距离是多少？
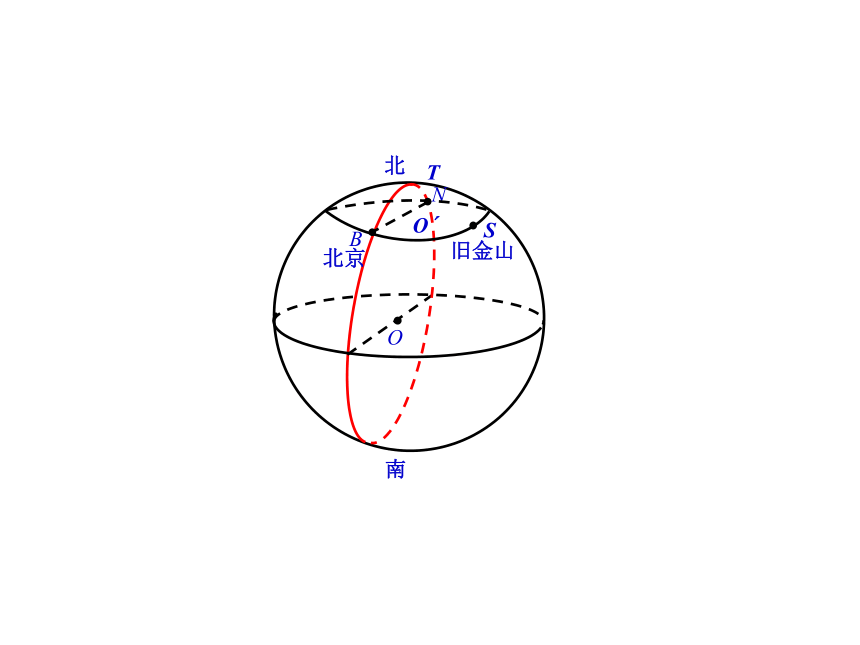
如下图，一架飞机从北京首都国际机场起飞，目的地是美国纽约肯尼迪国际机场，北京与纽约大致都在北纬40上，如果不考虑其他因素，飞机如何飞行才能使航程最短？
如上图，我们用点B代表北京、点N代表纽约，点O表示球心．用经过B点、 N点、 O点的平面去截球面，得到一个大圆（由于平面过球心），那么B点、 N点就把这个大圆分成两段圆弧，长的一段叫优弧，短的一段叫劣弧．
再回到上图，很容易得到，飞机沿着大圆从北京向北经极地飞行到达纽约，航程最短，它比飞机向东沿北纬40°的小圆，经旧金山到达纽约的航程要短．
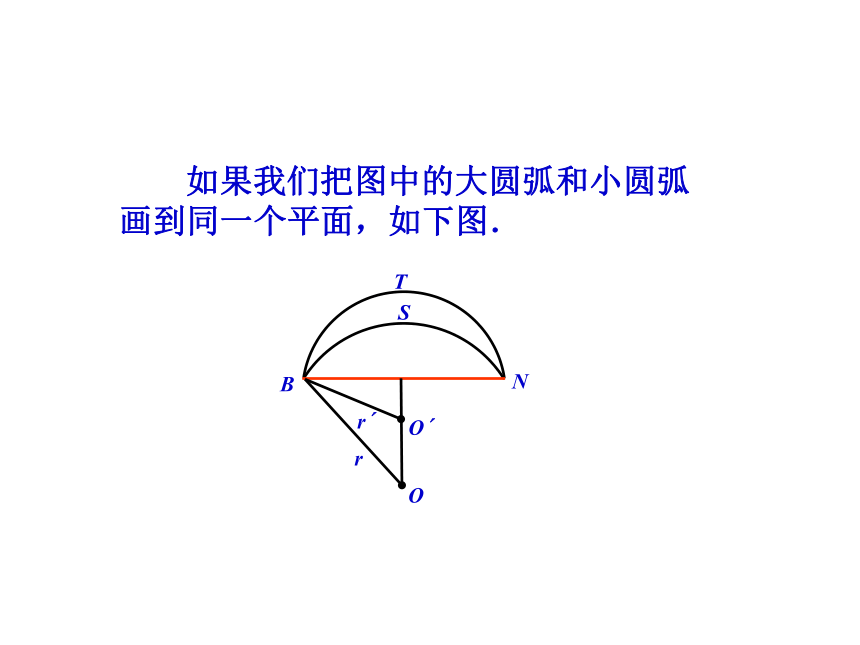
如果我们把图中的大圆弧和小圆弧画到同一个平面，如下图．
观察图形可知，以O为圆心，OB为半径的圆弧 ，比以点O为圆心，OB为半径的圆弧 要短．也就是说，平面上经过任意两点的劣弧中，半径越大，劣弧越短．
劣弧的长度是球面上两点之间的最短路径，我们把它称为球面上两点之间的距离．
因此过球面上两点一定可以连一条且只可以连一条大圆弧——劣弧．
例1 假设地球的半径为R，如图，在北纬45°的纬线上有A，B两点，且 所对的圆心角∠AO?B=90°，求球面上A，B两点间的距离．
解：如图，连结OA，OB，AB，OO?.由纬度的意义，可得

同理，
因为∠AO?B=90．
所以
又因为OA=OB=R，所以∠AOB=60，
因此，球面上A，B两点间的距离等于
由于不在同一条直线上的三点唯一确定一个圆，因此过球面上两点必可连一条大圆弧—劣弧．这类似平面上经过两点可以连一条直线，且只可能连一条直线；平面上两点之间的最短路径是线段．因此，球面上的大圆可以“扮演”平面上直线的角色．
尽管球面上的大圆可以“扮演”平面上直线的角色，但是两者之间也有很大的不同．平面上的两条直线可以相交：只有一个交点；也可以不相交（平行）：没有交点．但是球面上任意两个大圆（类似平面上的两条直线）必定相交，且有两个交点．
为什么两个大圆必定相交，且有两个交点？
如上图，因为球面上的两个大圆所在的平面都经过球心O．所以这两个大圆所在的平面有一个公共点，因此这两个平面必有一条过球心O的相交直线，这条相交直线显然是球面的直径所在的直线，两个大圆的交点是这条直径的两个端点A，A?．我们把球的直径的两个端点A，A?称为对径点．因此，两个大圆相交于对径点A，A?．
在平面上过一点A，做两条射线AB、AC，构成的图形叫做角记作∠BAC——平面上角的定义．
二、球面上的角
过球面上一点A，做两条大圆弧 、 ，它们构成图形是球面角．仍记为∠BAC,点A叫球面角的顶点，大圆弧 、 叫球面角的边，记为AB、AC．（结合下图）
类似地，我们可以定义球面上的角：
如何度量角∠BAC的大小？
如右图，球面角∠BAC的两边AB，AC延长后相交于点A的对径点A?．AB，AC所在大圆的半平面构成一个二面角B-AA?-C．显然，球面角∠BAC与二面角B-AA?-C唯一对应．
我们用二面角B-AA?-C来度量球面角∠BAC，而二面角B-AA?-C的大小可以用它的平面角来度量，这样球面角∠BAC的大小可以用平面上的角度来度量了．即在二面角B-AA?-C棱AA?上，如果我们在球心O处，分别作OD⊥AA?，OE⊥AA?，且他们分别交球面角∠BAC的两边AB，AC于D，E两点，那么∠DOE为二面角B-AA?-C的平面角.这时，用∠DOE的大小度量球面角∠BAC．
从另外一个角度看，如果点A处分别作大圆弧 和 得切线AB?和AC?，显然AB?⊥AA，OD⊥OA，且AB?和OD在同一个平面内，所以AB?‖OD．同理，AC?‖OE.所以，∠B?AC?=∠DOE.也就是说，∠DOE等于点A处分别与球面角∠BAC的两边AB和AC相切的射线AB?和AC?所成的角∠B?AC?．
由球面角的定义，我们再看一下经线经度的意义．如下图，地球球面上一点的经线是过该点的经线（半个大圆）所在半平面与过格林尼治天文台的经线所在半平面组成的二面角的大小．
实际上，为了考虑问题方便，二面角B-AA?-C平面角通常取为大圆的圆心角∠DOE．
点A在东经90的经线上，东经90的意义就是球面角∠BNC=90°．这个角我们也通常取为赤道所在大圆的圆心角，即∠BOC=90°．
例2 设地球的半径为R，且点A和点B分别表示地球赤道上的两个城市，它们的经度分别为东经30°和西经30°，那么它们之间的距离是多少？
解：如图，连结OA，OB，由经度的意义，我们知道，
∠AOB=30°+30°=60°=
因此，球面上A，B两点之间的距离为
1.由在平面上的距离引出球面上的距离的定义．
2.由平面上的角引出球面上的角的定义，以此来给出它的度量．