第三讲 球面上的基本图形

(共32张PPT)
我们在平面上除了学习直线和角之外，还学习三角形．
这次课学习球面上的基本图形
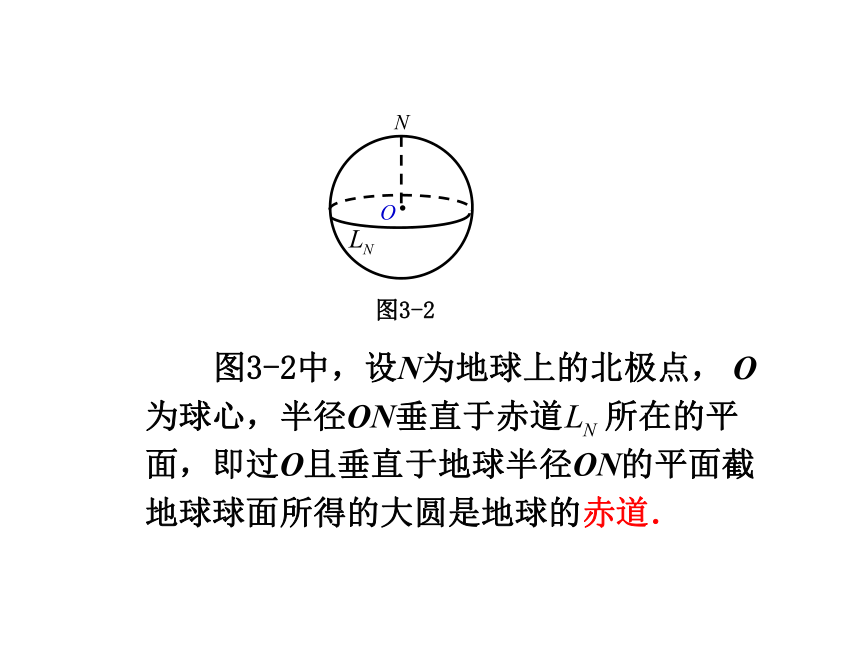
一、极与赤道
大家熟知，地球上有南极、北极、赤道．我们在球面几何中同样引入“极”、“赤道”的概念．
图3-2中，设N为地球上的北极点， O为球心，半径ON垂直于赤道 所在的平面，即过O且垂直于地球半径ON的平面截地球球面所得的大圆是地球的赤道．
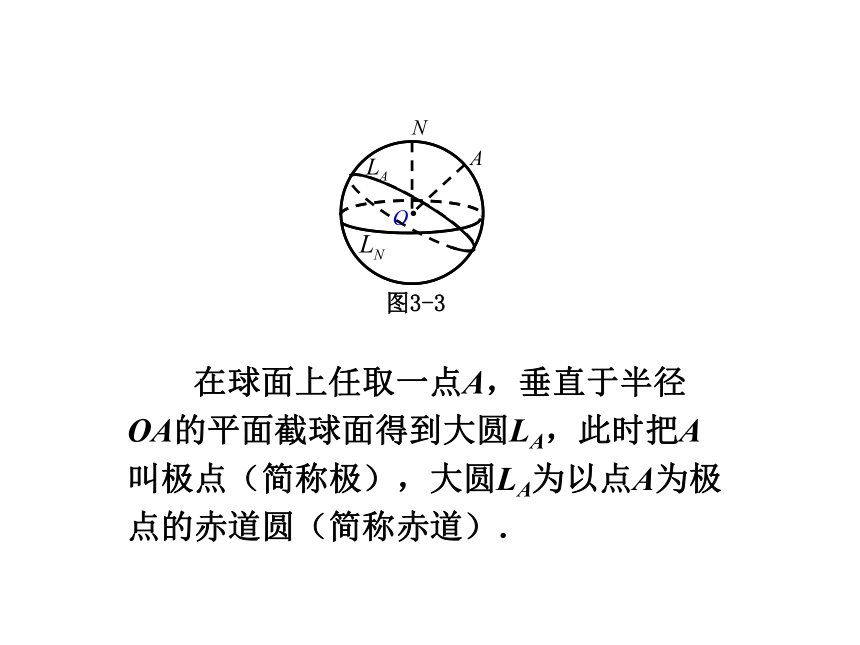
在球面上任取一点A，垂直于半径OA的平面截球面得到大圆LA，此时把A叫极点（简称极），大圆LA为以点A为极点的赤道圆（简称赤道）．
对于球面上任意一点，均可以得到与它对应的一个赤道;对于球面上的赤道，可以得到与它对应的两个极点．
由概念看出，极与赤道有着对应关系，那么两者之间除此之外，是否还有其他紧密的联系？
分析：如果球的半径为R，那么极点A与赤道上任一点B的距离为 ，（即 圆的周长），如下图所示：
由上面分析可知：
1、球面上与点A的距离为 的点必在赤道LA上．
2、球面上任一点A都对应它的一个赤道LA ，那么该点到赤道的距离均为 ．
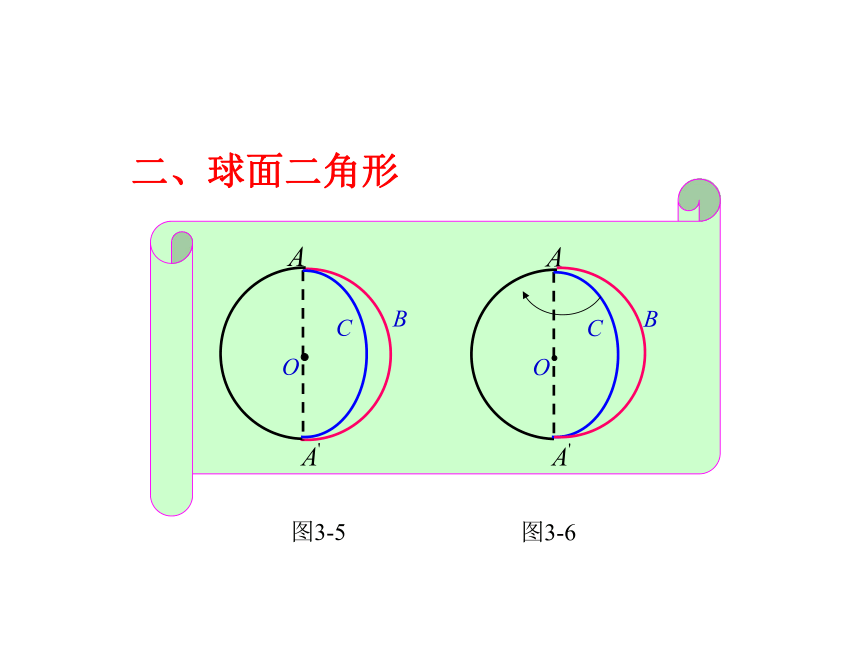
二、球面二角形
由图3-5知，球面角∠BAC的两边AB、AC延长后交于A?，所组成的图形ABA?C成为球面二角形．又称（月形）．
例1 如图3-6，已知球面角 ，求证：月形ABAC?的面积等于球面面积的 倍．
证明：将月形ABAC?中的一条边ACA?在球面上由右向左旋转到边ACA?的位置，则边ACA?扫过整个球面，边ACA?旋转了一周，故球面可以看作是球面角为 的月形．
若球面角 ，那么月形ABAC?的面积等于球面面积的 倍．
所以，
月形ABAC?面积= ．
三、球面三角形
１、球面三角形
前者是平面上的三角形，它是三条线段首位顺次相接构成的封闭图形．
完全类似，可以把球面上的三条“直线”（三条大圆的圆弧）首位顺次相接的封闭图形是球面三角形．（如图３-８）
思考
如何度量球面△ABC的边和内角？
如图，连接球心O与A、B、C三点，由球面角的定义及度量可知，球面△ABC的三个内角∠A、∠B、∠C可分别由二面角B-OA-C、A-OB-C、B-OC-A度量．
如果设 （ 均为弧度），那么球面△ABC的三边AB，BC，CA分别为：
．
其中r为球的半径．若r=1,则AB= ，BC= ，CA= ．
2、三面角
无论是测边长还是内角，都要连接球心与球面三角形的顶点（图3-9），如果延长上图中的三条线段OA、OB、OC使其成为射线，这三条射线构成三个平面，把这样的图形叫做三面角（图3-10），记为O-ABC．
O点为三面角的顶点，OA、OB、OC称为它的棱，∠AOB，∠BOC，∠COA称为它的面角．
相邻两面构成的二面角是三面角的二面角，一个三面角有三个二面角．
综上，球面△ABC的三个内角对应于三面角O-ABC的三个二面角，三条边对应三面角O-ABC的三个面角．
下面对应关系
我们可以利用三面角的知识研究球面三角形．
球面△ABC 三面角O-ABC
内角 二面角
边 面角
在球面上找到A、B、C关于球心O的对称点A?、B?、C?,以对称点为顶点构成的球面三角形△A?B?C?，成为球面三角形△ABC的对顶三角形（图3-11）．
3、对顶三角形
4、球极三角形
对于任意球面△ABC，假设与BC边所在大圆对应的极点为A?、A?，与边AC所在大圆对应的极点为B?、B?，与边AB所在大圆对应的极点为C?、C?．
上图中点A?与A，B?与B、C?与C，在同一个半球面内，称球面△A?B?C?为球面△ABC的极对称三角形，简称球极三角形.
如果球面△A?B?C?是球面△ABC的极对称三角形，那么球面△A?B?C?的极对称三角形是什么？
球面△A?B?C?的极对称三角形是球面△ABC．
总结：
球面△A?B?C?与它的球极△ABC互为极对称三角形．
动动脑
球面三角形与球极三角形之间还有其他关系吗？
假定球面为单位球面，有下面结论：若球面△ABC的极对称三角形是△A?B?C ?，且它们的内角（单位：弧度）与边长分别为∠A、∠B、∠C，a，b，c和∠A?、∠B?、∠C?，a?，b?，c?那么
1. 球面三角形
2. 三面角
3. 对顶三角形
4. 球极三角形