第四讲 球面三角形

(共25张PPT)
旧知回顾
在上一讲中，我们主要讲了球面上的基本图形．我们认识了球面二面角和球面三角形．回想一下球面三角形的定义和性质．
新课导入
本讲我们在类比平面三角形有关性质的基础上，讨论球面三角形三边之间的关系、球面“等腰”三角形、球面三角形的周长以及球面三角形的内角和等等．
一、球面三角形三边之间的关系
在平面上，三角形满足：
两边之和大于第三边；
两边之差小于第三边．
球面上是否也成立？
图4-1
由于引入三面角，对于球面上边与角的研究就转化为立体几何中角的研究．
球面三角形的边对应三面角的面角，因此研究三面角中三个面角之间的关系．
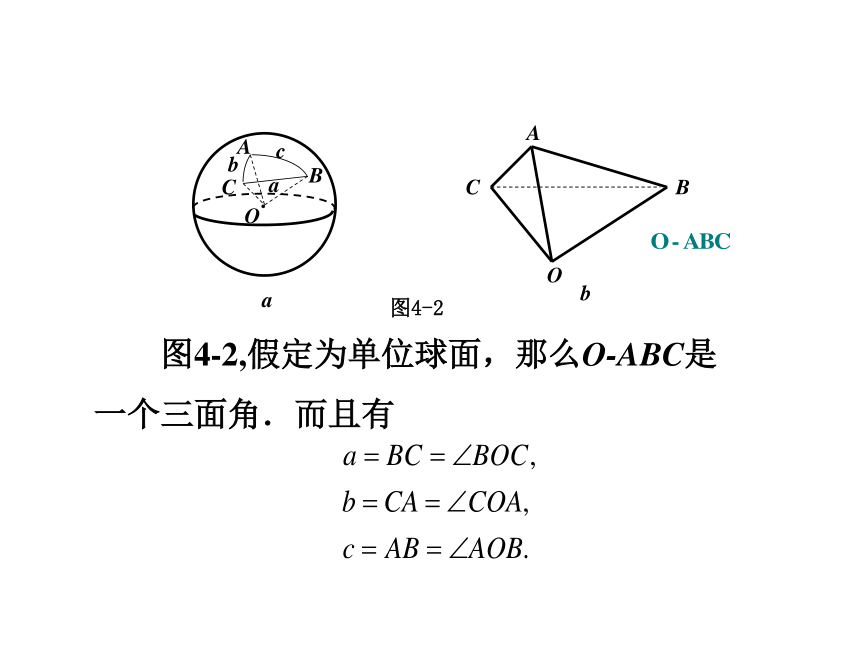
图4-2,假定为单位球面，那么O-ABC是一个三面角．而且有
在b图中，我们可以证明
再根据上述等式，得到
这样可以得出：
三面角中的两个面角之和大于第三个面角．
对应到球面三角形中，就有：
球面三角形中，两边之和大于第三边，两边之差小于第三边．
二、球面“等腰”三角形
类似平面三角形的两边相等，则对角相等．
在球面三角形中，等边对等角，等角对等边；大角对大边，大边对大角．
已知： 在球面△ABC中，b=c
求证:∠B=∠C．
动动脑
三 、球面三角形的周长
在球面三角形中，每条边都小于大圆周长的一半，所以周长不会超过3/2个大圆周长．
实际上，周长要小于大圆周长．
具体的证明方法是应用球面上边角对等的关系来验证的．
一个很重要的结论：球面三角形的周长小于大圆周长．
四、球面三角形的内角和
对于平面三角形，内角和等于180°．
那么球面三角形的内角和是否也是一个定值呢？
上图中，设A点表示地球的北极，B、C两点所在的曲线是赤道LA，其中，B点所在的经线是0°，C点所在经线是90°．AB、AC是两条经线，而经线与赤道平面垂直，所以∠BAC=π/2．
由极与赤道的概念知道：

因此三角形的内角和为
说明球面上存在内角和大于180°的三角形．
球面面积等于1/4上半球面面积（因为区域扫过了90°），也等于1/8球面面积，如果半径为r，那么球面△ABC的面积=
如果再在赤道上取一点D，所在的经线是东经120°，这是球面△ABD的面积又会是多少？
通过计算得：
球面△ABD面积
一般的，球面△ABC的半径为r,则任意球面的面积=（A+B+C-π）r2，(A、B、C分别为角A、B、C的弧度数)，特殊的，若半径为1，则面积=（A+B+C-π）．
通过例子说明球面三角形的内角和是大于180°的．
这是球面几何与欧氏几何不同的重要特征之一．
球面三角形的内角和是不是可以任意大？
图4-5
分析：由于球面三角形的内角所对应的边都小于大圆周长的一半，故每个内角都小于180°，所以内角和要小于540°，实际上，球面三角形的内角和要小于360°．
课堂小结
1. 球面三角形三边之间的关系；
2. 球面“等腰”三角形；
3. 球面三角形的周长以及球面三角
形的内角和；