高中数学人教新课标A版选修3-3第八讲 欧式几何与非欧几何(共34张PPT)
文档属性
| 名称 | 高中数学人教新课标A版选修3-3第八讲 欧式几何与非欧几何(共34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 753.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-09 10:57:28 | ||
图片预览











文档简介
(共34张PPT)
通过前面的学习,我们知道球面几何与平面几何中的许多定理是“相同”的,但也有一些定理是不相同的.
在本讲,我们首先通过平面几何与球面几何的比较,追溯某些定理不相同的根源,给出欧氏几何与非欧几何的定义;然后通过欧氏平行公理的分析,给出非欧几何的一种模型——庞加莱模型.
欧几里得
庞加莱
感知球面几何与平面几何的异同点.
认识非欧几何的特点.
了解庞加莱模型的内涵.
通过比较,了解平面几何与球面几何的异
同点.
进一步了解球面几何在实际生活中的应
用.
让学生从对比中学习知识.
从生活中大量存在的现象中总结规律.
培养合作交流意识.
球面几何与平面几何的比较.
非欧几何的概念和意义.
庞加莱模型.
一 平面几何与球面几何的比较
平面几何 球面几何
相
同的定理 1.平面(球面)三角形两边之和大于第三边.
2.若两个平面(球面)三角形的三对边对应相等,则两个三 角形全等.
3.若两个平面(球面)三角形的两对边对应相等,且其夹角对应相等,则两个三角形全等.
4.若两个平面(球面)三角形的两对角对应相等,且其夹边对应相等,则两个三角形全等.
5.平面(球面)“等腰”三角形的两底角相等,两腰对应相等.
…………….
平面几何 球面几何
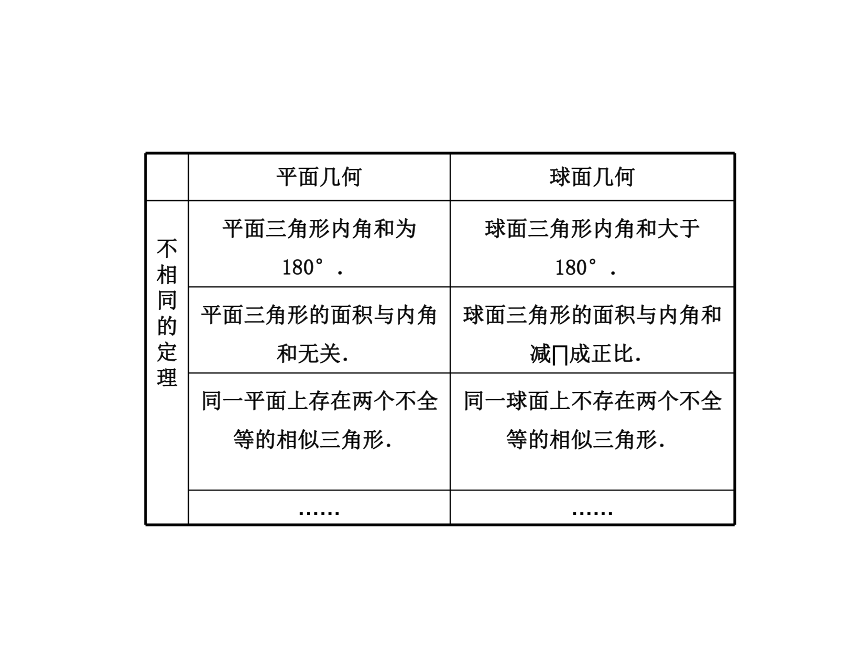
不相同的定理 平面三角形内角和为180°. 球面三角形内角和大于180°.
平面三角形的面积与内角和无关. 球面三角形的面积与内角和减∏成正比.
同一平面上存在两个不全等的相似三角形. 同一球面上不存在两个不全等的相似三角形.
…… ……
为什么会出现不同?
追溯其根源,是平面上有这样一个结论:
过直线外一点,有且只有一条直线与该直线不相交.
我们把两条不想交的直线称为平行线,上述结论最早出现在欧几里得所著的《原本》中,所以我们把上述结论称为欧氏平行公理.在欧氏平行公理成立的条件下,推导出来的所有定理及其他结果所组成的几何体系成为欧氏几何.
球面上的大圆可视为“直线”.在球面上有这样一个结论:任意两条“直线”(大圆)都相交,即过“直线”外一点,没有一条“直线”与该“直线”不相交.
也就是说,对球面上的大圆而言,欧氏平行公理是不成立的.于是,在球面上产生了一些与欧氏平面几何完全不同的定理.
在欧氏平行公理不成立的条件下,推导出来的所有定理与其结果所组成的几何体系,称为非欧几何.
二 欧氏平行公理与非欧几何模型
——庞加莱模型
在球面上欧氏平行公理不成立的原因,是我们把大圆当作“直线”,因此任意两条“直线”都相交.但是大圆是弯曲的,并非像直线一样是笔直的;大圆的长度是有限的,而直线的长度是可以无限增大的.
那么,为什么把大圆作为“直线”呢?
在球面上,大圆具有直线在平面上的一些最基本的性质.例如,过两点有且只有一条直线;两点之间的连线中直线最短,等等,这些性质球面上的大圆都具备.所以大圆可以作为直线所具有的基本性质的一种说明或解释,这种解释可以视为一种模型.
现在我们来分析一下欧氏平行公理:“过直线外一点,有且只有一条直线与该直线不相交.”在平面上欧氏平行公理是不证自明的.因为这个结论没有加以证明,所以我们当然可以怀疑它是否正确.
在球面上,如果我们把大圆作为“直线”,那么这个结论就不正确.这是一种怀疑方式,即“过直线外一点,没有一条直线与该直线不相交”.
我们还可以用另一种方式来怀疑它,即“过直线外一点,不只一条直线与该直线不相交”.我们把这样改变后的结论称为非欧(双曲)平行公理.有双曲平行公理成立的情况下,推导出来的所有定理所组成的几何体系称为双曲几何.
那么是否在某个特殊的“平面”上,可以把某种曲线叫作“直线”,此时,非欧平行公理是成立的,这个“平面”可作为非欧几何模型.
下面,我们给出法国数学家庞加莱建立的满足非欧平行公理的一种几何模型.
在欧氏平面上做一条直线x,以x为边缘的上半平面(不包含x 上的点)记为 (图8-1),现在考虑 内部的点,我们规定 内部
的点为“非欧点”,圆心在x上的半圆或垂直于x的射线称为“非欧直线”.
那么,在 内、圆心在x上的一段圆弧,或垂直于x的射线上的一条线段是“非欧线段”,两条“非欧直线”的夹角是“非欧角”.
这样,在 内部建立了一个非欧几何的模型,在此模型内满足:过直线外一点,不只一条直线与该直线不相交.
结合图8-1,我们具体说明如下:
设 l 为 内垂直于x的射线,或者圆心在x上的半圆,点A为 l 外的一点,则过点A必可作两个半圆(或一射线、一半圆),其圆心在x上,且与 l 相切(显然,切点在x上,而x上的点都不在 内),那么经过点A就有两条“非欧直线”与 l 都不相交,所以在内非欧平行公理是成立的.
当然,在这我们还需要说明两段“非欧线段”相等(或说合同)的概念、两个“非欧角”相等的概念等,这就要涉及其他的数学知识.这里就不再介绍了.
把“过直线外一点,没有一条直线与该直线不相交”作为公理推导出的几何称为椭圆几何.
非欧几何主要有椭圆几何和双曲几何,它们与欧氏几何有明显的差异.
上面模型是庞加莱模型,庞加莱模型是一个双曲几何的模型.
欧氏几何 椭圆几何 双曲几何
过直线外一点,有且只有一条直线与该直线不相交. 过直线外一点,没有一条直线与该直线不相交. 过直线外一点,不只一条直线与该直线不相交.
三角形内角和为180°. 三角形内角和大于180°. 三角形内角和小于180°.
三角形的面积与内角和无关. 三角形的面积与内角和减180°成正比. 三角形的面积与180°减内角和成正比.
当然,这三种几何也有相同的地方:
1. 三角形中两边之和大于第三边;
2. 若两个三角形的三对边对应相等,
则两个三角形全等.
三 欧氏几何与非欧几何的意义
欧氏平行公理与非欧平行公理看起来是相互矛盾的,在一般情况下,如果有两个互相矛盾的结论,则必定有一个是错误的,现在我们如何判断谁对谁错?
首先,判断一种几何是否正确的标准是什么?
1. 这种几何在理论上是否成立,这是本质上的逻辑问题;
2.这种几何在实际中是否成立,能否刻画我们生活的物理世界.
数学家用间接的方法,在欧氏几何中建立了一个非欧几何的模型,在这个模型中,规定了一些(非欧)基本概念后,全部的推理都是依照欧氏几何所遵循的逻辑进行的,因此这个模型是欧氏几何与非欧几何的一个“桥梁”.
非欧几何的结论通过模型又可解释为欧氏几何中的一个结论,这样一来,如果非欧几何是矛盾的,那么,欧氏几何在逻辑上也是矛盾的,因此,庞加莱模型告诉我们,如果欧氏几何是无矛盾的,那么非欧几何也是无矛盾的.
爱因斯坦认为,时间和空间是不可分的,物理空间十分复杂,无论欧氏几何或非欧几何都不能全面、精确的解释物理的时空概念,但他们都是物理空间,对物理空间在不同方面有很好的近似.因此,两者对于我们的世界有重要的物理意义.
作为本书的最后一讲,这里主要介绍了非欧几何的一种模型——庞加莱模型.最后简单介绍一下欧氏几何与非欧几何的意义.
通过前面的学习,我们知道球面几何与平面几何中的许多定理是“相同”的,但也有一些定理是不相同的.
在本讲,我们首先通过平面几何与球面几何的比较,追溯某些定理不相同的根源,给出欧氏几何与非欧几何的定义;然后通过欧氏平行公理的分析,给出非欧几何的一种模型——庞加莱模型.
欧几里得
庞加莱
感知球面几何与平面几何的异同点.
认识非欧几何的特点.
了解庞加莱模型的内涵.
通过比较,了解平面几何与球面几何的异
同点.
进一步了解球面几何在实际生活中的应
用.
让学生从对比中学习知识.
从生活中大量存在的现象中总结规律.
培养合作交流意识.
球面几何与平面几何的比较.
非欧几何的概念和意义.
庞加莱模型.
一 平面几何与球面几何的比较
平面几何 球面几何
相
同的定理 1.平面(球面)三角形两边之和大于第三边.
2.若两个平面(球面)三角形的三对边对应相等,则两个三 角形全等.
3.若两个平面(球面)三角形的两对边对应相等,且其夹角对应相等,则两个三角形全等.
4.若两个平面(球面)三角形的两对角对应相等,且其夹边对应相等,则两个三角形全等.
5.平面(球面)“等腰”三角形的两底角相等,两腰对应相等.
…………….
平面几何 球面几何
不相同的定理 平面三角形内角和为180°. 球面三角形内角和大于180°.
平面三角形的面积与内角和无关. 球面三角形的面积与内角和减∏成正比.
同一平面上存在两个不全等的相似三角形. 同一球面上不存在两个不全等的相似三角形.
…… ……
为什么会出现不同?
追溯其根源,是平面上有这样一个结论:
过直线外一点,有且只有一条直线与该直线不相交.
我们把两条不想交的直线称为平行线,上述结论最早出现在欧几里得所著的《原本》中,所以我们把上述结论称为欧氏平行公理.在欧氏平行公理成立的条件下,推导出来的所有定理及其他结果所组成的几何体系成为欧氏几何.
球面上的大圆可视为“直线”.在球面上有这样一个结论:任意两条“直线”(大圆)都相交,即过“直线”外一点,没有一条“直线”与该“直线”不相交.
也就是说,对球面上的大圆而言,欧氏平行公理是不成立的.于是,在球面上产生了一些与欧氏平面几何完全不同的定理.
在欧氏平行公理不成立的条件下,推导出来的所有定理与其结果所组成的几何体系,称为非欧几何.
二 欧氏平行公理与非欧几何模型
——庞加莱模型
在球面上欧氏平行公理不成立的原因,是我们把大圆当作“直线”,因此任意两条“直线”都相交.但是大圆是弯曲的,并非像直线一样是笔直的;大圆的长度是有限的,而直线的长度是可以无限增大的.
那么,为什么把大圆作为“直线”呢?
在球面上,大圆具有直线在平面上的一些最基本的性质.例如,过两点有且只有一条直线;两点之间的连线中直线最短,等等,这些性质球面上的大圆都具备.所以大圆可以作为直线所具有的基本性质的一种说明或解释,这种解释可以视为一种模型.
现在我们来分析一下欧氏平行公理:“过直线外一点,有且只有一条直线与该直线不相交.”在平面上欧氏平行公理是不证自明的.因为这个结论没有加以证明,所以我们当然可以怀疑它是否正确.
在球面上,如果我们把大圆作为“直线”,那么这个结论就不正确.这是一种怀疑方式,即“过直线外一点,没有一条直线与该直线不相交”.
我们还可以用另一种方式来怀疑它,即“过直线外一点,不只一条直线与该直线不相交”.我们把这样改变后的结论称为非欧(双曲)平行公理.有双曲平行公理成立的情况下,推导出来的所有定理所组成的几何体系称为双曲几何.
那么是否在某个特殊的“平面”上,可以把某种曲线叫作“直线”,此时,非欧平行公理是成立的,这个“平面”可作为非欧几何模型.
下面,我们给出法国数学家庞加莱建立的满足非欧平行公理的一种几何模型.
在欧氏平面上做一条直线x,以x为边缘的上半平面(不包含x 上的点)记为 (图8-1),现在考虑 内部的点,我们规定 内部
的点为“非欧点”,圆心在x上的半圆或垂直于x的射线称为“非欧直线”.
那么,在 内、圆心在x上的一段圆弧,或垂直于x的射线上的一条线段是“非欧线段”,两条“非欧直线”的夹角是“非欧角”.
这样,在 内部建立了一个非欧几何的模型,在此模型内满足:过直线外一点,不只一条直线与该直线不相交.
结合图8-1,我们具体说明如下:
设 l 为 内垂直于x的射线,或者圆心在x上的半圆,点A为 l 外的一点,则过点A必可作两个半圆(或一射线、一半圆),其圆心在x上,且与 l 相切(显然,切点在x上,而x上的点都不在 内),那么经过点A就有两条“非欧直线”与 l 都不相交,所以在内非欧平行公理是成立的.
当然,在这我们还需要说明两段“非欧线段”相等(或说合同)的概念、两个“非欧角”相等的概念等,这就要涉及其他的数学知识.这里就不再介绍了.
把“过直线外一点,没有一条直线与该直线不相交”作为公理推导出的几何称为椭圆几何.
非欧几何主要有椭圆几何和双曲几何,它们与欧氏几何有明显的差异.
上面模型是庞加莱模型,庞加莱模型是一个双曲几何的模型.
欧氏几何 椭圆几何 双曲几何
过直线外一点,有且只有一条直线与该直线不相交. 过直线外一点,没有一条直线与该直线不相交. 过直线外一点,不只一条直线与该直线不相交.
三角形内角和为180°. 三角形内角和大于180°. 三角形内角和小于180°.
三角形的面积与内角和无关. 三角形的面积与内角和减180°成正比. 三角形的面积与180°减内角和成正比.
当然,这三种几何也有相同的地方:
1. 三角形中两边之和大于第三边;
2. 若两个三角形的三对边对应相等,
则两个三角形全等.
三 欧氏几何与非欧几何的意义
欧氏平行公理与非欧平行公理看起来是相互矛盾的,在一般情况下,如果有两个互相矛盾的结论,则必定有一个是错误的,现在我们如何判断谁对谁错?
首先,判断一种几何是否正确的标准是什么?
1. 这种几何在理论上是否成立,这是本质上的逻辑问题;
2.这种几何在实际中是否成立,能否刻画我们生活的物理世界.
数学家用间接的方法,在欧氏几何中建立了一个非欧几何的模型,在这个模型中,规定了一些(非欧)基本概念后,全部的推理都是依照欧氏几何所遵循的逻辑进行的,因此这个模型是欧氏几何与非欧几何的一个“桥梁”.
非欧几何的结论通过模型又可解释为欧氏几何中的一个结论,这样一来,如果非欧几何是矛盾的,那么,欧氏几何在逻辑上也是矛盾的,因此,庞加莱模型告诉我们,如果欧氏几何是无矛盾的,那么非欧几何也是无矛盾的.
爱因斯坦认为,时间和空间是不可分的,物理空间十分复杂,无论欧氏几何或非欧几何都不能全面、精确的解释物理的时空概念,但他们都是物理空间,对物理空间在不同方面有很好的近似.因此,两者对于我们的世界有重要的物理意义.
作为本书的最后一讲,这里主要介绍了非欧几何的一种模型——庞加莱模型.最后简单介绍一下欧氏几何与非欧几何的意义.
同课章节目录
- 第一讲 从欧氏几何看球面
- 一 平面与球面的位置关系
- 二 直线与球面的位置关系和球幂定理
- 三 球面的对称性
- 第二讲 球面上的距离和角
- 一 球面上的距离
- 二 球面上的角
- 第三讲 球面上的基本图形
- 一 极与赤道
- 二 球面二角形
- 三 球面三角形
- 第四讲 球面三角形
- 一 球面三角形三边之间的关系
- 二 球面“等腰”三角形
- 三 球面三角形的周长
- 四 球面三角形的内角和
- 第五讲 球面三角形的全等
- 1.“边边边”(s.s.s)判定定理
- 2.“边角边”(s.a.s.)判定定理
- 3.“角边角”(a.s.a.)判定定理
- 4.“角角角”(a.a.a.)判定定理
- 第六讲 球面多边形与欧拉公式
- 一 球面多边形及其内角和公式
- 二 简单多面体的欧拉公式
- 三 用球面多边形的内角和公式证明欧拉公式
- 第七讲 球面三角形的边角关系
- 一 球面上的正弦定理和余弦定理
- 二 用向量方法证明球面上的余弦定理
- 三 从球面上的正弦定理看球面与平面
- 四 球面上余弦定理的应用──求地球上两城市间的距离
- 第八讲 欧氏几何与非欧几何
- 一 平面几何与球面几何的比较
- 二 欧氏平行公理与非欧几何模型──庞加莱模型
- 三 欧氏几何与非欧几何的意义
