浙教版七年级数学下册1.5 图形的平移课件(共40张PPT)
文档属性
| 名称 | 浙教版七年级数学下册1.5 图形的平移课件(共40张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-10 00:00:00 | ||
图片预览








文档简介
(共40张PPT)
1.5图形的平移
null
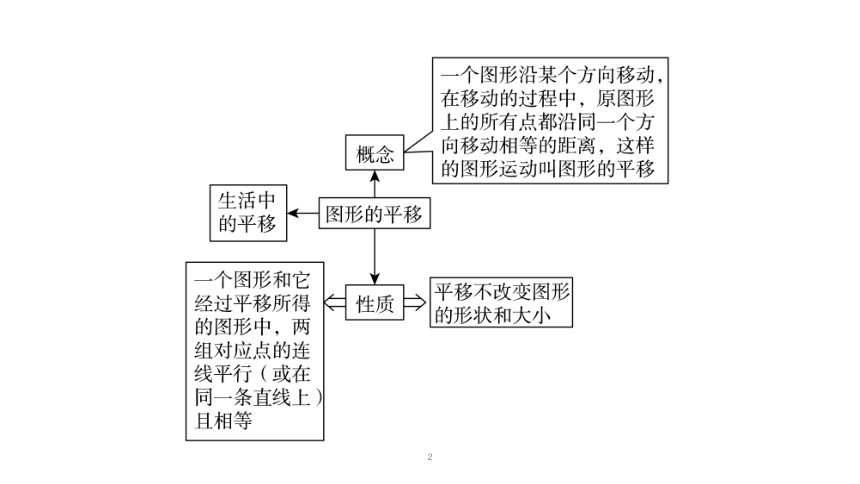
平移变换的概念:
平移变换:由一个图形变换为另一个图形,在改变的过程中,原图形上所有的点都沿同一个方向运动,且运动相等的距离,这样的图形运动叫做图形的平移,简称平移.
平移变换的条件:(1)相同的运动方向;(2)相等的运动距离.
知识点聚焦:
null
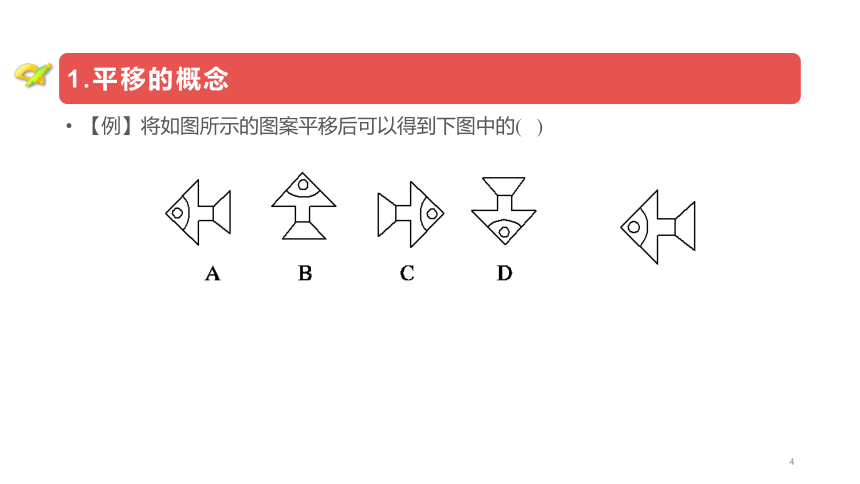
【例】将如图所示的图案平移后可以得到下图中的( )
1.平移的概念
null
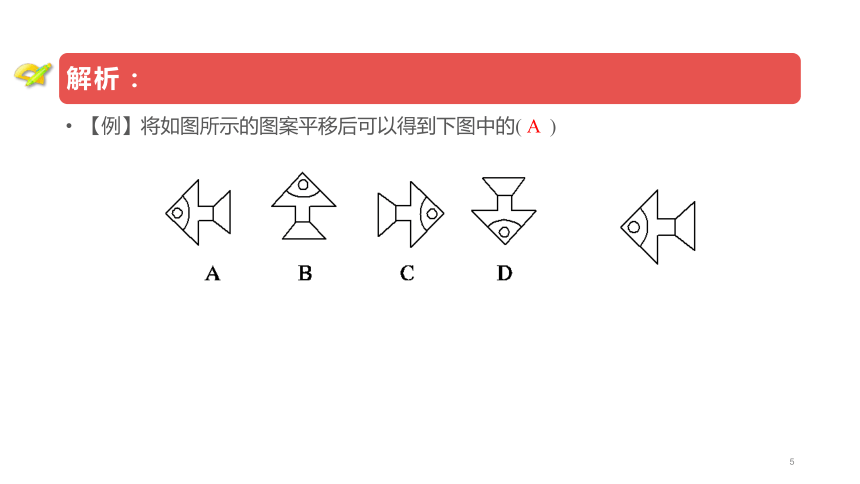
【例】将如图所示的图案平移后可以得到下图中的( A )
解析:
null
【例】如图,在10×6的网格中,每个小方格的边长都是1个单位,将△ABC平移到△DEF的位置,下面正确的平移步骤是( )
A.先把△ABC向左平移5个单位,再向下平移2个单位
B.先把△ABC向右平移5个单位,再向下平移2个单位
C.先把△ABC向左平移5个单位,再向上平移2个单位
D.先把△ABC向右平移5个单位,再向上平移2个单位
1.平移的概念
null
【例】如图,在10×6的网格中,每个小方格的边长都是1个单位,将△ABC平移到△DEF的位置,下面正确的平移步骤是( A )
A.先把△ABC向左平移5个单位,再向下平移2个单位
B.先把△ABC向右平移5个单位,再向下平移2个单位
C.先把△ABC向左平移5个单位,再向上平移2个单位
D.先把△ABC向右平移5个单位,再向上平移2个单位
解析:
null
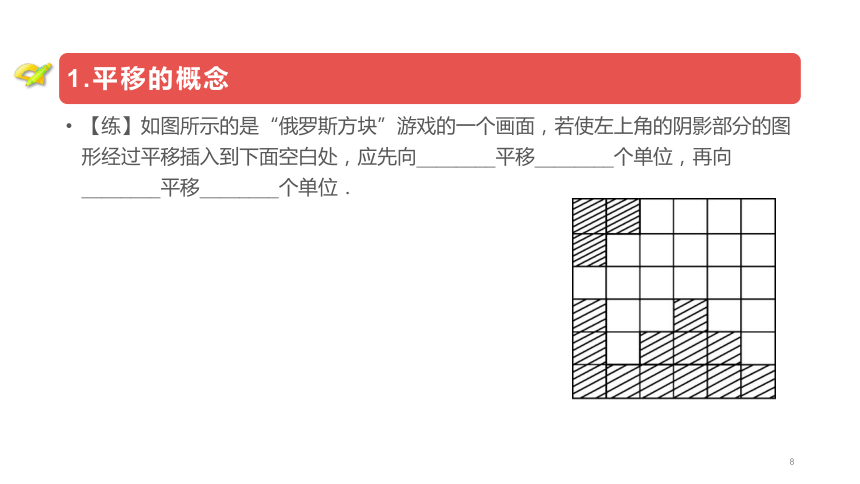
【练】如图所示的是“俄罗斯方块”游戏的一个画面,若使左上角的阴影部分的图形经过平移插入到下面空白处,应先向________平移________个单位,再向________平移________个单位.
1.平移的概念
null
【练】如图所示的是“俄罗斯方块”游戏的一个画面,若使左上角的阴影部分的图形经过平移插入到下面空白处,应先向右平移1个单位,再向下平移3个单位.
解析:
null
平移变换的性质:
性质:(1)平移变换不改变图形的形状和大小.
(2)一个图形和它经过平移所得的图形中,两组对应点的连线平行
(或在同一条直线上)且相等.
[注意] 平移的基本性质从局部刻画了平移过程中的不变因素,它是作图的依据.
知识点聚焦:
null
【例】下列说法:①△ABC在平移过程中,对应线段一定相等;②△ABC在平移过程中,对应线段一定平行或共线;③△ABC在平移过程中,周长不变;④△ABC在平移过程中,面积不变.其中正确的有( )
A.①②③ B.①②④ C.①③④ D.①②③④
2.平移变换的性质
null
【例】下列说法:①△ABC在平移过程中,对应线段一定相等;②△ABC在平移过程中,对应线段一定平行或共线;③△ABC在平移过程中,周长不变;④△ABC在平移过程中,面积不变.其中正确的有( D )
A.①②③ B.①②④ C.①③④ D.①②③④
解析:
null
【例】如图所示,△DBC是由△EAF平移得到的,且平移距离为AF,则图中与线段AB相等的线段分别是____________.
2.平移变换的性质
null
【例】如图所示,△DBC是由△EAF平移得到的,且平移距离为AF,则图中与线段AB相等的线段分别是____________.
【解析】平移后对应点的连线平行且相等,可知与线段AB相等的线段有三条,
分别是线段BF,FC,ED.
【答案】BF,FC,ED
解析:
null
【练】如图,将周长为8的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为 ( )
A.6 B.8 C.10 D.12
2.平移变换的性质
null
【练】如图,将周长为8的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为 ( )
A.6 B.8 C.10 D.12
【解析】将周长为8的△ABC沿边BC向右平移1个单位得到△DEF,
∴AD=1,BF=BC+CF=BC+1,DF=AC.
又∵AB+BC+AC=8,
∴四边形ABFD的周长为AD+AB+BF+DF=1+AB+BC+1+AC=10.
【答案】C
解析:
null
【练】白云宾馆在装修时,准备在主楼梯上铺上红地毯.已知这种地毯每平方米售价30元,主楼梯宽2米,其侧面如图所示,则购买这种地毯至少需要 元.
2.平移变换的性质
null
【分析】根据题意,结合图形,先把楼梯的横竖向上向右平移,构成一个矩形,再
求得其面积,则购买地毯的钱数可求.
【解析】如图,利用平移线段,把楼梯的横竖向上向右平移,构成一个矩形,
长宽分别为5.8米,2.6米,
即可得地毯的长度为2.6+5.8=8.4(米),地毯的面积为8.4×2=16.8(平方米),
故买地毯至少需要16.8×30=504(元).
【答案】504.
解析:
null
【拓展】如图(1),两个等边△ABD,△CBD的边长均为1,将△ABD沿AC方向向右平移到△A′B′D′的位置,得到图(2),则阴影部分的周长为____.
2.平移变换的性质
null
【拓展】如图(1),两个等边△ABD,△CBD的边长均为1,将△ABD沿AC方向向右平移到△A′B′D′的位置,得到图(2),则阴影部分的周长为____.
【解析】平移后得到六个角的三角形都是等边三角形,不一定全等,阴影部
分的用长即为原三角形的两条边长之和,为2。
【答案】2
解析:
null
【例】如图,直径为4 cm的圆O1平移5 cm到圆O1 ,则图中阴影部分的面积为________ cm2.
2.平移变换的性质
null
【例】如图,直径为4 cm的圆O1平移5 cm到圆O1 ,则图中阴影部分的面积为________ cm2.
【答案】 20
【点拨】用圆O1的右半圆替换圆O2的右半圆,转为求举行的面积
解析:
null
【例】如图所示是重叠的两个直角三角形.将其中一个直角三角形沿BC方向平移得到△DEF.如果AB=8 cm,BE=4 cm,DH=3 cm,求图中阴影部分的面积.
2.平移变换的性质
null
【解析】由平移可得DE=AB=8 cm,∴EH=5 cm.
∵S△ABC=S△DEF,
∴S△ABC-S△EHC=S△DEF-S△EHC,即S四边形ABEH=S四边形DHCF.
∵S四边形ABEH=×(5+8)×4=26(cm2),
∴图中阴影部分的面积为26 cm2.
解析:
null
【练】如图,将面积为5的△ABC沿BC方向平移至△DEF的位置,平移的距离是边BC长的两倍,那么图中的四边形ACED的面积为 .
2.平移变换的性质
null
【解析】设点A到BC的距离为h,则S△ABC=BC·h=5.
∵平移的距离是BC的长的2倍,
∴AD=2BC,CE=BC,
∴四边形ACED的面积为(AD+CE)·h= (2BC+BC)·h=3× BC·h=3×5=15.
【答案】15
解析:
null
【例】如图,某居民小区有一长方形地,居民想在长方形地内修筑同样宽的两条小路,余下部分绿化,道路的宽为2米,则绿化的面积为多少平方米?
2.平移变换的性质
null
【例】如图,某居民小区有一长方形地,居民想在长方形地内修筑同样宽的两条小路,余下部分绿化,道路的宽为2米,则绿化的面积为多少平方米?
【分析】平移后可得道路的长和宽,再利用矩形的面积公式进行计算即可.
【解析】平移后得绿化部分宽为(20﹣2)米,长为(32﹣2)米,
面积为(20﹣2)×(32﹣2)=18×30=540(平方米).
答:则绿化的面积为540平方米.
解析:
null
【拓展】(1)图①是将线段AB向右平移1个单位长度,图②是将线段AB折一下再向右平移1个单位长度,请在图③中画出一条有两个折点的折线向右平移1个单位长度的图形.
(2)若长方形的长为a,宽为b,请分别写出三个图形中除去阴影部分后剩余部分的面积.
(3)如图④,在宽为10m,长为40m的长方形菜地上有一条弯曲的小路,小路宽为1m,求这块菜地的面积.
2.平移变换的性质
null
【分析】(1)根据两个折点,可得小路是三个平行四边形;
(2)根据路的形状是矩形,可得路的面积,根据面积的和差,可得答案;
(3)根据等底等高的面积相等,可得路的面积,根据面积的和差,可得答案.
【解析】(1)如图:
(2)三个图形中除去阴影部分后剩余部分的面积:①ab﹣b;②ab﹣b;③ab﹣b;
(3)40×10﹣10×1=390(m2).
答:这块菜地的面积是390m2.
解析:
null
【例】如图,已知△ABC的面积为16,BC的长为8,现将△ABC沿BC向右平移m个单位到△A'B'C'的位置.若四边形ABB'A'的面积为32,求m的值。
2.平移变换的性质
null
【解析】如图,过点A向BC作垂线,垂足为H,
∵△ABC的面积=16,BC=8,∴BCAH=16,
∴ ×8×AH=16,解得AH=4,
又∵四边形ABB'A'的面积为32,
∴BB' ×4=32,∴BB'=32÷4=8,
∴m=BB' =8,即m的值是8。
解析:
null
(1)平移作图的要点:
①平移的方向; ②平移的距离.
知识点聚焦:
null
(2)图形平移的几种基本类型与画法:
①点的平移:以已知点为一个端点,按要求的方向和距离作线段,则线段另一端的点即为所求;
②线段的平移:先平移线段的两个端点,再连结这两点即可;
③角的平移:通过三个点(顶点、两边上各取一点)的平移来实现;
④多边形的平移:按要求的平移方式平移各顶点,然后用线段顺次连结即可;
⑤圆的平移:通过平移圆心,然后以原来圆的半径为半径作圆来实现.
知识点聚焦:
null
【例】如图所示,经过平移,∠ABC的顶点B移到了点D,作出平移后的∠D;
3.平移作图
null
【例】如图所示,经过平移,∠ABC的顶点B移到了点D,作出平移后的∠D;
【点拨】过点D作射线DE∥AB,DF∥BC,则∠D即为所求;
解析:
null
【练】将如图所示的图形按箭头所指的方向平移3 cm,作出平移后的图形.
3.平移作图
null
【练】将如图所示的图形按箭头所指的方向平移3 cm,作出平移后的图形.
【点拨】只要确定六个关键点平移后的位置,
就可以作出符合要求的图形.
解析:
null
【练】如图,方格中有一条可爱的小金鱼.
(1)若小方格的边长均为1,则小金鱼的面积为________;
(2)画出小金鱼向左平移3格后的图形(不要求写画法).
3.平移作图
null
【练】如图,方格中有一条可爱的小金鱼.
(1)若小方格的边长均为1,则小金鱼的面积为________;
(2)画出小金鱼向左平移3格后的图形(不要求写画法).
【分析】(1)可将小金鱼分割成3个三角形来求;
(2)将每个关键点向左平移3格,顺次连结各点即可.
【解析】(1)小金鱼的面积为×4×5+ ×4×2+ ×2×2=16.
(2)图略.
解析:
null
1.5图形的平移
null
平移变换的概念:
平移变换:由一个图形变换为另一个图形,在改变的过程中,原图形上所有的点都沿同一个方向运动,且运动相等的距离,这样的图形运动叫做图形的平移,简称平移.
平移变换的条件:(1)相同的运动方向;(2)相等的运动距离.
知识点聚焦:
null
【例】将如图所示的图案平移后可以得到下图中的( )
1.平移的概念
null
【例】将如图所示的图案平移后可以得到下图中的( A )
解析:
null
【例】如图,在10×6的网格中,每个小方格的边长都是1个单位,将△ABC平移到△DEF的位置,下面正确的平移步骤是( )
A.先把△ABC向左平移5个单位,再向下平移2个单位
B.先把△ABC向右平移5个单位,再向下平移2个单位
C.先把△ABC向左平移5个单位,再向上平移2个单位
D.先把△ABC向右平移5个单位,再向上平移2个单位
1.平移的概念
null
【例】如图,在10×6的网格中,每个小方格的边长都是1个单位,将△ABC平移到△DEF的位置,下面正确的平移步骤是( A )
A.先把△ABC向左平移5个单位,再向下平移2个单位
B.先把△ABC向右平移5个单位,再向下平移2个单位
C.先把△ABC向左平移5个单位,再向上平移2个单位
D.先把△ABC向右平移5个单位,再向上平移2个单位
解析:
null
【练】如图所示的是“俄罗斯方块”游戏的一个画面,若使左上角的阴影部分的图形经过平移插入到下面空白处,应先向________平移________个单位,再向________平移________个单位.
1.平移的概念
null
【练】如图所示的是“俄罗斯方块”游戏的一个画面,若使左上角的阴影部分的图形经过平移插入到下面空白处,应先向右平移1个单位,再向下平移3个单位.
解析:
null
平移变换的性质:
性质:(1)平移变换不改变图形的形状和大小.
(2)一个图形和它经过平移所得的图形中,两组对应点的连线平行
(或在同一条直线上)且相等.
[注意] 平移的基本性质从局部刻画了平移过程中的不变因素,它是作图的依据.
知识点聚焦:
null
【例】下列说法:①△ABC在平移过程中,对应线段一定相等;②△ABC在平移过程中,对应线段一定平行或共线;③△ABC在平移过程中,周长不变;④△ABC在平移过程中,面积不变.其中正确的有( )
A.①②③ B.①②④ C.①③④ D.①②③④
2.平移变换的性质
null
【例】下列说法:①△ABC在平移过程中,对应线段一定相等;②△ABC在平移过程中,对应线段一定平行或共线;③△ABC在平移过程中,周长不变;④△ABC在平移过程中,面积不变.其中正确的有( D )
A.①②③ B.①②④ C.①③④ D.①②③④
解析:
null
【例】如图所示,△DBC是由△EAF平移得到的,且平移距离为AF,则图中与线段AB相等的线段分别是____________.
2.平移变换的性质
null
【例】如图所示,△DBC是由△EAF平移得到的,且平移距离为AF,则图中与线段AB相等的线段分别是____________.
【解析】平移后对应点的连线平行且相等,可知与线段AB相等的线段有三条,
分别是线段BF,FC,ED.
【答案】BF,FC,ED
解析:
null
【练】如图,将周长为8的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为 ( )
A.6 B.8 C.10 D.12
2.平移变换的性质
null
【练】如图,将周长为8的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为 ( )
A.6 B.8 C.10 D.12
【解析】将周长为8的△ABC沿边BC向右平移1个单位得到△DEF,
∴AD=1,BF=BC+CF=BC+1,DF=AC.
又∵AB+BC+AC=8,
∴四边形ABFD的周长为AD+AB+BF+DF=1+AB+BC+1+AC=10.
【答案】C
解析:
null
【练】白云宾馆在装修时,准备在主楼梯上铺上红地毯.已知这种地毯每平方米售价30元,主楼梯宽2米,其侧面如图所示,则购买这种地毯至少需要 元.
2.平移变换的性质
null
【分析】根据题意,结合图形,先把楼梯的横竖向上向右平移,构成一个矩形,再
求得其面积,则购买地毯的钱数可求.
【解析】如图,利用平移线段,把楼梯的横竖向上向右平移,构成一个矩形,
长宽分别为5.8米,2.6米,
即可得地毯的长度为2.6+5.8=8.4(米),地毯的面积为8.4×2=16.8(平方米),
故买地毯至少需要16.8×30=504(元).
【答案】504.
解析:
null
【拓展】如图(1),两个等边△ABD,△CBD的边长均为1,将△ABD沿AC方向向右平移到△A′B′D′的位置,得到图(2),则阴影部分的周长为____.
2.平移变换的性质
null
【拓展】如图(1),两个等边△ABD,△CBD的边长均为1,将△ABD沿AC方向向右平移到△A′B′D′的位置,得到图(2),则阴影部分的周长为____.
【解析】平移后得到六个角的三角形都是等边三角形,不一定全等,阴影部
分的用长即为原三角形的两条边长之和,为2。
【答案】2
解析:
null
【例】如图,直径为4 cm的圆O1平移5 cm到圆O1 ,则图中阴影部分的面积为________ cm2.
2.平移变换的性质
null
【例】如图,直径为4 cm的圆O1平移5 cm到圆O1 ,则图中阴影部分的面积为________ cm2.
【答案】 20
【点拨】用圆O1的右半圆替换圆O2的右半圆,转为求举行的面积
解析:
null
【例】如图所示是重叠的两个直角三角形.将其中一个直角三角形沿BC方向平移得到△DEF.如果AB=8 cm,BE=4 cm,DH=3 cm,求图中阴影部分的面积.
2.平移变换的性质
null
【解析】由平移可得DE=AB=8 cm,∴EH=5 cm.
∵S△ABC=S△DEF,
∴S△ABC-S△EHC=S△DEF-S△EHC,即S四边形ABEH=S四边形DHCF.
∵S四边形ABEH=×(5+8)×4=26(cm2),
∴图中阴影部分的面积为26 cm2.
解析:
null
【练】如图,将面积为5的△ABC沿BC方向平移至△DEF的位置,平移的距离是边BC长的两倍,那么图中的四边形ACED的面积为 .
2.平移变换的性质
null
【解析】设点A到BC的距离为h,则S△ABC=BC·h=5.
∵平移的距离是BC的长的2倍,
∴AD=2BC,CE=BC,
∴四边形ACED的面积为(AD+CE)·h= (2BC+BC)·h=3× BC·h=3×5=15.
【答案】15
解析:
null
【例】如图,某居民小区有一长方形地,居民想在长方形地内修筑同样宽的两条小路,余下部分绿化,道路的宽为2米,则绿化的面积为多少平方米?
2.平移变换的性质
null
【例】如图,某居民小区有一长方形地,居民想在长方形地内修筑同样宽的两条小路,余下部分绿化,道路的宽为2米,则绿化的面积为多少平方米?
【分析】平移后可得道路的长和宽,再利用矩形的面积公式进行计算即可.
【解析】平移后得绿化部分宽为(20﹣2)米,长为(32﹣2)米,
面积为(20﹣2)×(32﹣2)=18×30=540(平方米).
答:则绿化的面积为540平方米.
解析:
null
【拓展】(1)图①是将线段AB向右平移1个单位长度,图②是将线段AB折一下再向右平移1个单位长度,请在图③中画出一条有两个折点的折线向右平移1个单位长度的图形.
(2)若长方形的长为a,宽为b,请分别写出三个图形中除去阴影部分后剩余部分的面积.
(3)如图④,在宽为10m,长为40m的长方形菜地上有一条弯曲的小路,小路宽为1m,求这块菜地的面积.
2.平移变换的性质
null
【分析】(1)根据两个折点,可得小路是三个平行四边形;
(2)根据路的形状是矩形,可得路的面积,根据面积的和差,可得答案;
(3)根据等底等高的面积相等,可得路的面积,根据面积的和差,可得答案.
【解析】(1)如图:
(2)三个图形中除去阴影部分后剩余部分的面积:①ab﹣b;②ab﹣b;③ab﹣b;
(3)40×10﹣10×1=390(m2).
答:这块菜地的面积是390m2.
解析:
null
【例】如图,已知△ABC的面积为16,BC的长为8,现将△ABC沿BC向右平移m个单位到△A'B'C'的位置.若四边形ABB'A'的面积为32,求m的值。
2.平移变换的性质
null
【解析】如图,过点A向BC作垂线,垂足为H,
∵△ABC的面积=16,BC=8,∴BCAH=16,
∴ ×8×AH=16,解得AH=4,
又∵四边形ABB'A'的面积为32,
∴BB' ×4=32,∴BB'=32÷4=8,
∴m=BB' =8,即m的值是8。
解析:
null
(1)平移作图的要点:
①平移的方向; ②平移的距离.
知识点聚焦:
null
(2)图形平移的几种基本类型与画法:
①点的平移:以已知点为一个端点,按要求的方向和距离作线段,则线段另一端的点即为所求;
②线段的平移:先平移线段的两个端点,再连结这两点即可;
③角的平移:通过三个点(顶点、两边上各取一点)的平移来实现;
④多边形的平移:按要求的平移方式平移各顶点,然后用线段顺次连结即可;
⑤圆的平移:通过平移圆心,然后以原来圆的半径为半径作圆来实现.
知识点聚焦:
null
【例】如图所示,经过平移,∠ABC的顶点B移到了点D,作出平移后的∠D;
3.平移作图
null
【例】如图所示,经过平移,∠ABC的顶点B移到了点D,作出平移后的∠D;
【点拨】过点D作射线DE∥AB,DF∥BC,则∠D即为所求;
解析:
null
【练】将如图所示的图形按箭头所指的方向平移3 cm,作出平移后的图形.
3.平移作图
null
【练】将如图所示的图形按箭头所指的方向平移3 cm,作出平移后的图形.
【点拨】只要确定六个关键点平移后的位置,
就可以作出符合要求的图形.
解析:
null
【练】如图,方格中有一条可爱的小金鱼.
(1)若小方格的边长均为1,则小金鱼的面积为________;
(2)画出小金鱼向左平移3格后的图形(不要求写画法).
3.平移作图
null
【练】如图,方格中有一条可爱的小金鱼.
(1)若小方格的边长均为1,则小金鱼的面积为________;
(2)画出小金鱼向左平移3格后的图形(不要求写画法).
【分析】(1)可将小金鱼分割成3个三角形来求;
(2)将每个关键点向左平移3格,顺次连结各点即可.
【解析】(1)小金鱼的面积为×4×5+ ×4×2+ ×2×2=16.
(2)图略.
解析:
null
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
