第二章 二元一次方程组单元测试A卷(含解析)
文档属性
| 名称 | 第二章 二元一次方程组单元测试A卷(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-15 21:24:49 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
二元一次方程组单元测试A卷
一、选择题
方程,,,,中,二元一次方程的个数是
A. 5个 B. 4个 C. 3个 D. 2个
对于三元一次方程组,我们一般是先消去一个未知数,转化为二元一次方程组求解.那么在解三元一次方程组时,下列没行实现这一转化的是
A. B. C. D.
如果,且,那么的值为
A. B. C. D.
一副三角板按如图方式摆放,且的度数比的度数大,若设,,则可得到方程组为
A.
B.
C.
D.
陈老师打算购买气球装扮学校“六一”儿童节活动会场,气球的种类有“笑脸”和“爱心”两种,两种气球的价格不同,但同一种气球的价格相同,由于会场布置的需要,购买时以一束个气球为单位,已知第一、二束气球的价格如图所示,则第三束气球的价格为?
A. 14元 B. 15元 C. 16元 D. 17元
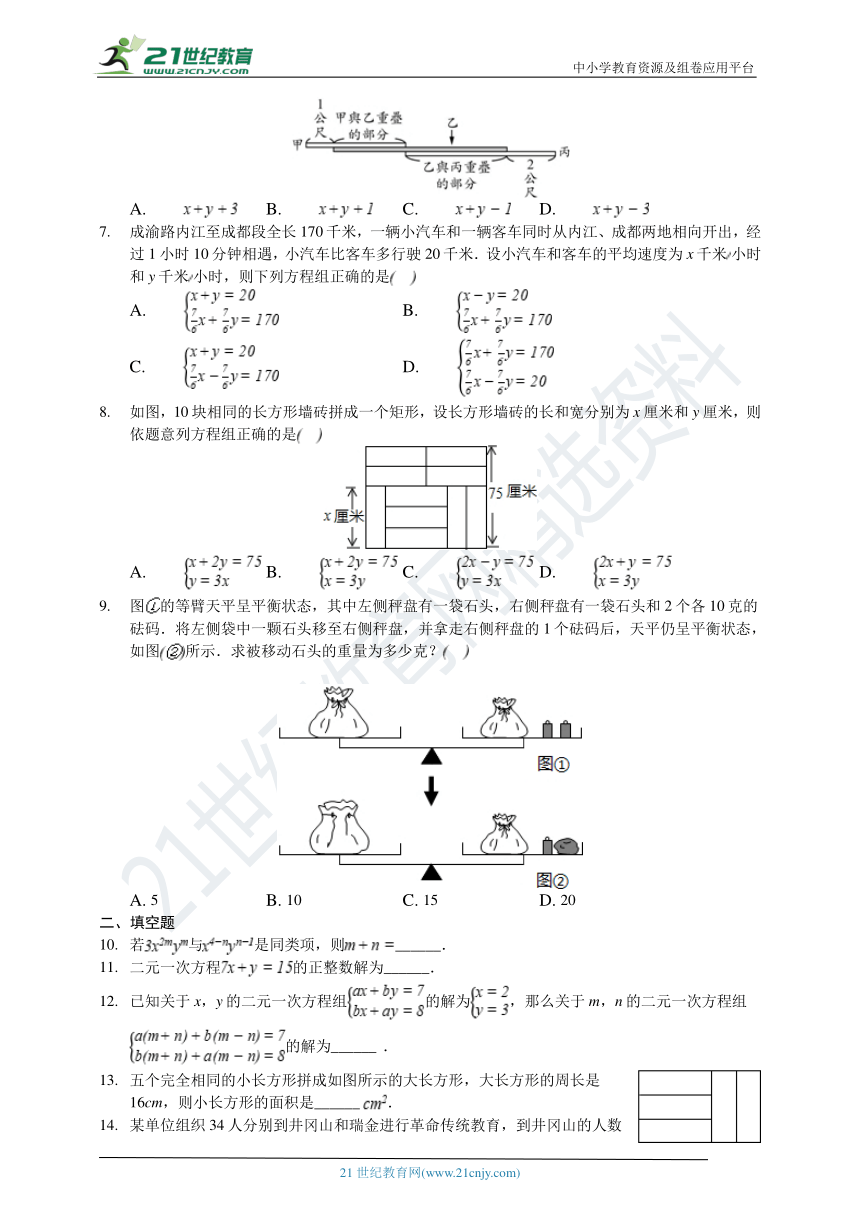
如图为甲、乙、丙三根笔直的木棍平行摆放在地面上的情形.已知乙有一部分只与甲重迭,其余部分只与丙重迭,甲没有与乙重迭的部分的长度为1公尺,丙没有与乙重迭的部分的长度为2公尺.若乙的长度最长且甲、乙的长度相差x公尺,乙、丙的长度相差y公尺,则乙的长度为多少公尺?
A. B. C. D.
成渝路内江至成都段全长170千米,一辆小汽车和一辆客车同时从内江、成都两地相向开出,经过1小时10分钟相遇,小汽车比客车多行驶20千米.设小汽车和客车的平均速度为x千米小时和y千米小时,则下列方程组正确的是
A. B.
C. D.
如图,10块相同的长方形墙砖拼成一个矩形,设长方形墙砖的长和宽分别为x厘米和y厘米,则依题意列方程组正确的是
A. B. C. D.
图的等臂天平呈平衡状态,其中左侧秤盘有一袋石头,右侧秤盘有一袋石头和2个各10克的砝码.将左侧袋中一颗石头移至右侧秤盘,并拿走右侧秤盘的1个砝码后,天平仍呈平衡状态,如图所示.求被移动石头的重量为多少克?
A. 5 B. 10 C. 15 D. 20
二、填空题
若与是同类项,则______.
二元一次方程的正整数解为______.
已知关于x,y的二元一次方程组的解为,那么关于m,n的二元一次方程组的解为______ .
五个完全相同的小长方形拼成如图所示的大长方形,大长方形的周长是16cm,则小长方形的面积是______?.
某单位组织34人分别到井冈山和瑞金进行革命传统教育,到井冈山的人数是到瑞金的人数的2倍多1人,求到两地的人数各是多少?设到井冈山的人数为x人,到瑞金的人数为y人,请列出满足题意的方程组______.
一艘轮船顺水航行的速度是20海里小时,逆水航行的速度是16海里小时,则水流的速度是______ 海里小时.
5月份,甲、乙两个工厂用水量共为200吨.进入夏季用水高峰期后,两工厂积极响应国家号召,采取节水措施月份,甲工厂用水量比5月份减少了,乙工厂用水量比5月份减少了,两个工厂6月份用水量共为174吨,求两个工厂5月份的用水量各是多少.设甲工厂5月份用水量为x吨,乙工厂5月份用水量为y吨,根据题意列关于x,y的方程组为______.
三、解答题
某校规划在一块长AD为18m,宽AB为13m的长方形场地ABCD上,设计分别与AD,AB平行的横向通道和纵向通道,其余部分铺上草皮.
如图1,若设计三条通道,一条横向,两条纵向,且它们的宽度相等,其余六块草坪相同,其中一块草坪两边之比,问通道的宽是多少?
为了建造花坛,要修改中的方案,如图2,将三条通道改为两条通道,纵向的宽度改为横向宽度的2倍,其余四块草坪相同,且每一块草坪均有一边长为8m,这样能在这些草坪建造花坛.如图3,在草坪RPCQ中,已知于点E,于点F,求花坛RECF的面积.
P表示n边形对角线的交点个数指落在其内部的交点,如果这些交点都不重合,那么P与n的关系式是
其中a,b是常数,
填空:通过画图可得:
四边形时,______填数字;五边形时,______填数字
请根据四边形和五边形对角线的交点个数,结合关系式,求a和b的值.注:本题中的多边形均指凸多边形
小华从家里到学校的路是一段平路和一段下坡路,假设他始终保持平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,则他从家里到学校需10min,从学校到家里需问:从小华家到学校的平路和下坡路各有多远?
假如娄底市的出租车是这样收费的:起步价所包含的路程为千米,超过千米的部分按每千米另收费.
小刘说:“我乘出租车从市政府到娄底汽车站走了千米,付车费元.”
小李说:“我乘出租车从市政府到娄底汽车站走了千米,付车费元.”
问:出租车的起步价是多少元?超过千米后每千米收费多少元?
??? 小张乘出租车从市政府到娄底南站高铁站走了千米,应付车费多少元?
某景点的门票价格如表:
购票人数人 100以上
每人门票价元 12 10 8
某校七年级、两班计划去游览该景点,其中班人数少于50人,班人数多于50人且少于100人,如果两班都以班为单位单独购票,则一共支付1118元;如果两班联合起来作为一个团体购票,则只需花费816元.
两个班各有多少名学生?
团体购票与单独购票相比较,两个班各节约了多少钱?
答案和解析
1.【答案】D
分析:
本题主要考查的是二元一次方程的定义,掌握二元一次方程的定义是解题的关键含有两个未知数,并且含有未知数的项的次数都是1,像这样的方程叫做二元一次方程根据定义可判断.
【解答】
解:不是整式方程,不是二元一次方程;
是二元一次方程;
,xy是二次,故不是二元一次方程;
是二元一次方程;
,是二次,故不是二元一次方程.
故选D.
2.【答案】A
解:因为解三元一次方程组的步骤先消去一个未知数,得到一个二元一次方程组,
所以没行实现这一转化的是A选项,仍旧是三个未知数,
故选:A.
根据解三元一次方程组的步骤先消去一个未知数,得到一个二元一次方程组,从而得出答案.
本题考查了三元一次方程组的解法,把“三元”转化为“二元”、把“二元”转化为“一元”的消元的思想方法,从而进一步理解把“未知”转化为“已知”和把复杂问题转化为简单问题的思想方法.解三元一次方程组的关键是消元.
3.【答案】A
分析:
本题考查用加减法解二元一次方程组,关键是掌握两个方程中含有三个未知数,为不定方程组,只能用一个未知数来表示另外两个未知数,然后化简即可.根据原题中虽然有三个未知数,但是可把和组成方程组,把其中的z当成已知量,解关于x,y的方程组,得x、y用含有z的代数式来表示,即可求出的值.
【解答】
解:,
得,
即,
所以.
故选A.
4.【答案】C
解:根据平角和直角定义,得方程;
根据比的度数大,得方程.
可列方程组为,
故选:C.
此题中的等量关系有:
三角板中最大的角是,从图中可看出;
比的度数大,则.
此题考查了学生对二元一次方程组的灵活运用,学生应该重视培养对应用题的理解能力,准确地列出二元一次方程组.
5.【答案】A
解:设笑脸形的气球x元一个,爱心形的气球y元一个,由题意,得:
,
解得:.
故选:A.
要求出第三束气球的价格,先求出笑脸形和爱心形的气球的单价就可以求出结论.
此题考查二元一次方程组解实际问题的运用和数学整体思想的运用,解答本题时根据单价数量总价的数量关系建立方程是关键.
6.【答案】A
解:设乙的长度为a公尺,
乙的长度最长且甲、乙的长度相差x公尺,乙、丙的长度相差y公尺,
甲的长度为:公尺;丙的长度为:公尺,
甲与乙重叠的部分长度为:公尺;乙与丙重叠的部分长度为:公尺,
由图可知:甲与乙重叠的部分长度乙与丙重叠的部分长度乙的长度,
,
,
,
,
乙的长度为:公尺,
故选:A.
设乙的长度为a公尺,则甲的长度为:公尺;丙的长度为:公尺,甲与乙重叠的部分长度为:公尺;乙与丙重叠的部分长度为:公尺,由图可知:甲与乙重叠的部分长度乙与丙重叠的部分长度乙的长度,列出方程,即可解答.
本题考查了考查了二元一次方程的应用,解决本题的关键是根据图形找到等量关系,列方程.
7.【答案】D
解:设小汽车和客车的平均速度为x千米小时和y千米小时,
由题意得,.
故选:D.
根据等量关系:相遇时两车走的路程之和为170千米,相遇时,小汽车比客车多行驶20千米,可得出方程组.
本题考查了由实际问题抽象二元一次方程组的知识,解答本题的关键是仔细审题得到等量关系,根据等量关系建立方程.
8.【答案】B
解:根据图示可得,
故选:B.
根据图示可得:矩形的宽可以表示为,宽又是75厘米,故,矩的长可以表示为2x,或,故,整理得,联立两个方程即可.
此题主要考查了由实际问题抽象出二元一次方程组,关键是看懂图示,分别表示出长方形的长和宽.
9.【答案】A
解:设左天平的一袋石头重x克,右天平的一袋石头重y克,被移动的石头重z克,由题意,得:
,
解得:.
故选:A.
设左天平的一袋石头重x克,右天平的一袋石头重y克,被移动的石头重z千克,根据题意及图象可以得出方程及,由两个方程构成方程组求出其解即可.
本题考查了列三元一次方程组解实际问题的运用,三元一次方程组的解法的运用,解答时理解图象天平反映的意义找到等量关系是关键.
10.【答案】3
解:与是同类项,
,
解得:
则.
故答案为:3.
直接利用同类项的定义得出关于m,n的等式,进而求出答案.
此题主要考查了同类项,正确把握同类项的定义是解题关键.
11.【答案】或
解:方程,
解得:,
,;,,
则方程的正整数解为或.
故答案为:或
把x看做已知数表示出y,即可求出正整数解.
此题考查了解二元一次方程,解题的关键是将x看做已知数求出y.
12.【答案】
解:关于x,y的二元一次方程组的解为,
,
,
解得,
故答案为:.
把代入可得,进而可得,再解即可.
此题主要考查了二元一次方程组的解,当遇到有关二元一次方程组的解的问题时,要回到定义中去,通常采用代入法,即将解代入原方程组,这种方法主要用在求方程中的字母系数.
13.【答案】3
解:设小长方形的长为xcm,宽为ycm,
根据题意得:,
解得:,
小长方形的面积为
故答案为:3.
设小长方形的长为xcm,宽为ycm,根据大长方形的周长结合图形可得出关于x、y的二元一次方程组,解之即可得出x、y的值,再根据长方形的面积公式即可得出结论.
本题考查了二元一次方程组的应用、长方形的周长及面积,根据数量关系列出关于x、y的二元一次方程组是解题的关键.
14.【答案】
解:设到井冈山的人数为x人,到瑞金的人数为y人,由题意得:
,
故答案为:.
根据关键语句“单位组织34人分别到井冈山和瑞金进行革命传统教育”可得方程,“到井冈山的人数是到瑞金的人数的2倍多1人”可得,联立两个方程即可.
此题主要考查了由实际问题抽象出二元一次方程组,关键是正确理解题意,抓住关键语句,列出方程.
15.【答案】2
解:顺水航行的速度是20海里小时,逆水航行的速度是16海里小时,
水流的速度是海里小时;
故答案为:2.
根据在水流问题中,水流速度顺水速度逆水速度,即可得出答案.
此题考查了水流问题在实际生活中的应用,解决问题的关键是读懂题意,找到所求的量的等量关系,水流速度顺水速度逆水速度.
16.【答案】
解:设甲工厂5月份用水量为x吨,乙工厂5月份用水量为y吨,
根据题意得:.
故答案为:.
设甲工厂5月份用水量为x吨,乙工厂5月份用水量为y吨,根据两厂5月份的用水量及6月份的用水量,即可得出关于x、y的二元一次方程组,此题得解.
本题考查了二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.
17.【答案】解:设通道的宽为xm,,
::9,
,
解得:.
答:通道的宽是1m;
四块相同草坪中的每一块,有一条边长为8m,若,则,不合题意,
,
纵向通道的宽为2m,横向通道的宽为1m,
,
,四边形RPCQ是长方形,
,
,
,
,
,
同理可得:,
,
,
即花坛RECF的面积为,
【解析】此题主要考查了二元一次方程组的应用即四边形面积求法和三角形面积求法等知识,得出RP的长是解题关键.
利用AM::9,设通道的宽为xm,,则,进而利用AD为18m,宽AB为13m得出等式求出即可;根据题意得出纵向通道的宽为2m,横向通道的宽为1m,进而得出PQ,RE的长,即可得出PE、EF的长,进而求出花坛RECF的面积.
18.【答案】1;5
解:如图所示:四边形时,;五边形时,;
故答案为:1,5;
由得:,
整理得:,
解得:.
根据题意画出图形,进而得出四边形和五边形中P的值;
利用中所求,得出二元一次方程组进而求出即可.
此题主要考查了二元一次方程组的应用,根据题意得出正确关于a,b的等量关系是解题关键.
19.【答案】解:设平路有xm,下坡路有ym,
根据题意得,
解得:,
答:小华家到学校的平路和下坡路各为300m,400m.
【解析】设出平路和坡路的路程,从家里到学校走平路和下坡路一共用10分钟,从学校到家里走上坡路和平路一共用15分钟,利用这两个关系式列出方程组解答即可.
本题考查了二元一次方程的应用,此题主要利用时间、速度、路程三者之间的关系解答,注意来回坡路的变化是解题的关键.
20.【答案】解:设出租车的起步价是x元,超过千米后每千米收费y元.
依题意得,,
解得.
答:出租车的起步价是元,超过千米后每千米收费2元;
元.
答:小张乘出租车从市政府到娄底南站高铁站走了千米,应付车费元.
【解析】设出租车的起步价是x元,超过千米后每千米收费y元.根据他们的对话列出方程组并解答;
千米分两段收费:千米、千米.根据中的单价进行计算.
本题考查了二元一次方程组的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.利用二元一次方程组求解的应用题一般情况下题中要给出2个等量关系,准确的找到等量关系并用方程组表示出来是解题的关键.
21.【答案】解:若不超过100人时,设人数为w人,则有,则w不是整数,不合题意,故两个班学生人数之和超过100人;设七年级班有x人、七年级班有y人,由题意,得
,
解得:.
答:七年级班有49人、七年级班有53人;
七年级班节省的费用为:元,
七年级班节省的费用为:元.
【解析】设七年级班有x人、七年级班有y人,根据如果两班都以班为单位单独购票,则一共支付1118元;如果两班联合起来作为一个团体购票,则只需花费816元建立方程组求出其解即可;
用一张票节省的费用该班人数即可求解.
本题考查了列二元一次方程组解实际问题的运用,二元一次方程组的解法的运用,解答时建立方程组求出各班的人数是关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
