浙教版数学七年级下册第5章分式导学案无答案
文档属性
| 名称 | 浙教版数学七年级下册第5章分式导学案无答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 716.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-27 10:47:26 | ||
图片预览




文档简介
课题 5、1分式
主备人 集体备课时间 上课时间
学习目标 1、了解分式的概念. 2、了解分式有意义的条件. 3、会用分式表示简单实际问题中的数量关系.
学习重点 学习难点 重点:分式的概念 难点:例2的问题情境较为复杂,并且涉及到分式、求分式的值等问题
学习过程 学教记录
【自主预学】:认真阅读课本P114至P115,回答下列问题(1、由数与字母或字母与字母相乘组成的代数式叫做__________.由几个单项式相加组成的代数式叫做__________.单项式、多项式统称为___________.2、分数的分母不能为_________,当分母为________时,分数没有意义. 【课堂导学】:(一)根据下列条件列出代数式 1、小明家距离学校2千米,从家骑车出发以25千米/小时的速度到学校,需__ _小时.2、班级篮球赛中,某班花了400元购买了m件男式汗衫和n件女式汗衫,那么平均每件汗衫的成本价是 元. 3、在校首届辩论赛中,102班的5位同学参加了辩论,共发言x次,那么每位辩手平均发言_______次.4、在“校园之星”展出活动中,每块展板的面积为s ,长为x,则宽为________. 5、捐书活动共有a人参加,其中男生共捐b本书,女生共捐c本书,那么平均每人捐出 本书. 6、为了调查珍稀动物资源,动物专家在p平方千米的保护区内找到了7只灰熊,则该保护区内平均每平方千米内有 只灰熊。归纳:表示两个______相除,且__________中含有字母的代数式叫做分式.(二)做一做、书本第114页思考: 1、如何判断一个代数式是不是分式? 2、分式中的字母能取任何实数吗?(三)例1、已知分式. 当x取什么数时,分式有意义? 当x取什么数时,分式的值为零? 当x=1时,分式的值是多少? 变式 已知分式.当x_______时,分式无意义; 当x_______时,分式的值为零. 归纳: 1、分式有意义的条件是_____________________________. 2、分式值为零的条件是_____________________________. (四) 例2、甲﹑乙两人从一条公路的某处出发,同向而行.已知甲每时行a千米,乙每时行b千米,a>b.如果乙提前1时出发,那么甲追上乙需要多少时间?当a=6,b=5时,求甲追上乙所需要的时间? 【分层助学】:1、当x___________时,分式有意义; 2、当x_________时,分式的值为零; 3、当x_________时,分式有意义. 4、已知分式,请在-2,0,1中任意选一个你喜欢的x代入求值.【课外拓展】1、某厂的仓库里有煤p吨,每天需用煤q(q>1)吨.若从现在开始,每天节省1吨煤,则p吨煤可用多少天?当p=10,q=3时,仓库里的煤可用几天?2、已知汽车的速度为v千米/时,甲、乙两地的路程是s千米。 该汽车行驶t小时的路程是 千米,从甲地到乙地需 行驶 小时。 如果该汽车的速度加快a千米/时,那么从甲地到乙地需 行驶 小时,加快后比加快前少用 小时。 3、 要使分式 没有意义,则x的值是 。4、要使分式 取值 有意义,那么x的取值为 。 【课后作业】:作业本 【反思促学】:
课题 5.2分式基本性质(1)
主备人 集体备课时间 上课时间
学习目标 1、理解分式的基本性质. 2、会进行分式的约分.
学习重点 学习难点 重点:分式的基本性质. 难点:例1第(2)题的约分过程.
学习过程 学教记录
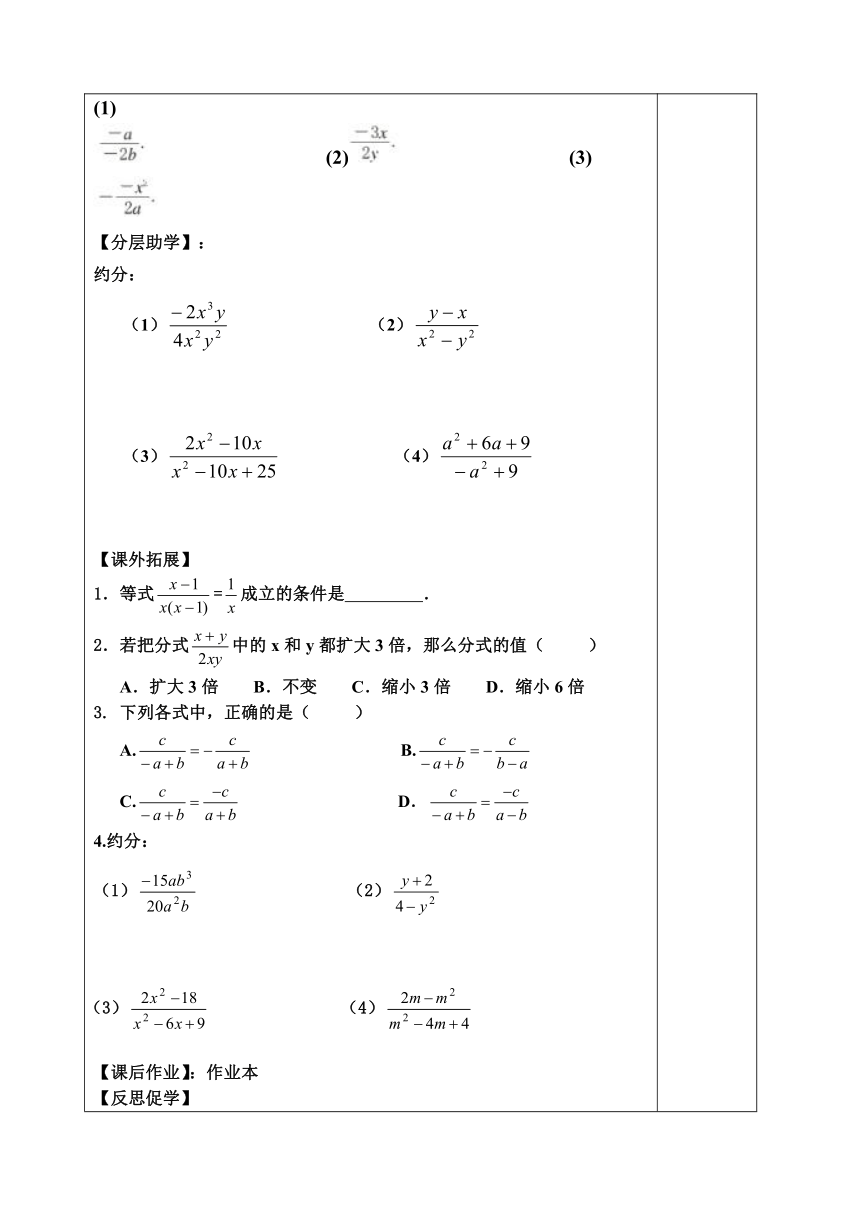
【自主预学】:认真阅读课本P117至P118,回答下列问题下面这些式子成立吗?依据是什么?== == 你能讲出分数的基本性质,类似地,分式也有以下基本性质:1.分式也有以下基本性质: 分式的分子与分母都乘以(或除以)同一个 的整式,分式的值不变。 2.用式子表示为 = ,= (其中M是不等于零的 ) 3.分式的约分:把一个分式的分子与分母的 约去,叫做分式的约分4.分子、分母没有公因式的分式叫做最简分式。(约分要约去分子、分母中 分因式。5、分式的符号性质:==( )=( ). 【课堂导学】:例1、化简下列分式: (1) (2) 2、不改变分式的值,把下列各式的分子与分母中的各项子数都化为整数。 (1) eq \f (x+y,x-y) (2) 2、不改变分式的值,使下列分式的分子与分母都不含“-”号.(1) ?????????????????????? (2)??????????????????? ? (3)【分层助学】:约分: (1) (2) (3) (4) 【课外拓展】 1.等式=成立的条件是 . 2.若把分式中的x和y都扩大3倍,那么分式的值( )A.扩大3倍 B.不变 C.缩小3倍 D.缩小6倍3. 下列各式中,正确的是( ) A. B. C. D. 4.约分:(1) (2) (3) (4) 【课后作业】:作业本 【反思促学】
课题 5.2分式基本性质(2)
主备人 集体备课时间 上课时间
学习目标 进一步掌握分式的基本性质及其应用. 会在已知等式的情况下将分式化简或求值,体验等量替换、整体代换的数学思想的方法. 3、会应用分式的约分进行多项式的除法。
学习重点 学习难点 重点:运用分式的约分进行多项式的除法. 难点:在已知等式的情况下将分式化简或求值.
学习过程 学教记录
【自主预学】:认真阅读课本P20至P121,回答下列问题一、复习巩固1.约分。 (1) (2) 2.已知m-3n=0,求分式的值 【课堂导学】:例2.已知 ,求分式 的值。 练一练P120课内练习1、2 例3.(1) (2) 两个多项式相除可以先表示成分式,通过因式分解、约分等把分式化简,用整式或最简分式表示商。【分层助学】:1计算 (1)(4a+a)÷(4a+1) (2)(x+2x)÷(x+2) (3)(3m+3m)÷(1-m) (4)(3xy-6xy)÷(2y-x) 2完成课本P121作业题.【课外拓展】 1.若=2,则= . 2.计算:(x-18x+81)÷(x+6x+9) 3.已知a+=2,求a+的值. 已知+=5,求的值. 【课后作业】:作业本 【反思促学】
课题 5.3分式的乘除
主备人 集体备课时间 上课时间
学习目标 1、掌握分式的乘除法则2、会进行分式的乘除运算,并会用来解决简单的实际问题。
学习重点 学习难点 重点:分式的乘除法则难点:例1 第(3)题的计算过程比较复杂,有一定的困难。
学习过程 学教记录
【自主预学】:认真阅读课本P121至P123,回答下列问题1.你能完成下列运算吗? 2、类比上面的分数乘除法运算,猜一猜 【课堂导学】:1.小组活动:(1)运算的根据是什么? (2)类比分数的乘除法法则,你能说出分式的乘除法法则吗?乘法法则:分式乘分式,用____________作为积的分子,_____________作为积的分母除法法则:分式除以分式,把_____________________________后,再与____________相乘。用式子表示为:_____________________________________________2、相信你能做对! (1) (2) (3) (4)例1:计算:(1) (2) (3) (4) 例2 一个长、宽、高分别为l,b,h的长方形纸箱装满了一层高为h的圆柱形易拉罐(如图).求纸箱空间的利用率(易拉罐总体积与纸箱容积的比,结果精确到1%). 3知识梳理:分式的乘除法运算要注意:(1) 分式的分子、分母是多项式时,一般要要先 后再进行乘法计算;。(2) 分式的乘除法运算顺序是 ;(3) 若分式与整式相乘除,应把整式看作是分母为 的式子; (4)计算的结果一定是 .【分层助学】:1、下列各式正确的是( )A. B. C. D.2、化简分式后得( )A.-a+b; B.-a-b; C.a-b; D.a+b3、计算(1) (2)【课外拓展】已知==≠0,求的值. 【课后作业】:作业本 【反思促学】:
课题 5.4分式的加减(1)
主备人 集体备课时间 上课时间
学习目标 掌握同分母分式加减的法则 会进行同分母分式的加减运算
学习重点 学习难点 重点:同分母分式的加减运算 难点:例2涉及两个分式的分母需作适当转化后才能运用同分母分式的加减法则是本节学习的难点。
学习过程 学教记录
【自主预学】:认真阅读课本P125至P126,回答下列问题1.计算: 类似地, _________,_________, 结论:同分母分式相加减,分母 ,把分子 。 2做一做 【课堂导学】:1.填空: (1) , (2) 。2、例1计算: (1) (2) 思考:这两题的中的两个分式同分母吗?3、练习(1) (2) (3) 4.完成课本P126课内练习1、2.例2先化简,再求值:其中x=3问:两个分式是否同分母?怎么化成同分母呢? 【分层助学】:1.计算:(1) , (2) , (3) , (4) 。 2、先化简,在求值:,其中m=2011,n=-1.【课外拓展】已知 (1)化简P、Q; (2)请你选择自己喜欢的一组的值,分别代入求P、Q的值; (3)比较P、Q的大小,并说明理由。 【课后作业】:作业本 【课后作业】:
课题 5.4分式的加减(2)
主备人 集体备课时间 上课时间
学习目标 学会异分母分式的通分 学会异分母分式的加减运算
学习重点 学习难点 重点:异分母分式的加减运算 难点:通分的过程是本节学习的难点。
学习过程 学教记录
【自主预学】:认真阅读课本P127至P128,回答下列问题1.先化简,再计算: ,其中x =6 。 2.计算根据异分母分数的加减法法则计算: 1)-= (2) 1--= 2) 对照上面的计算,完成下列填空:(1)+=+= (2)-=-( )= 什么叫做通分: 【课堂导学】:1.议一议:你能通过分式的通分,完成下面的填空吗? ; . 2、例3 计算: (1) (2) (3) 公分母: 公分母: 公分母: 3、例4 计算,并求当时原式的值。 【分层助学】:计算 (5) (6) 化简,并选择你喜欢的a值代入,求出原式的值。 【课外拓展】 【课后作业】: 【反思促学】
课题 5.5分式的方程(1)
主备人 集体备课时间 上课时间
学习目标 1、会根据定义判别分式方程与整式方程,了解分式方程增根产生的原因,掌握验根的方法。 2、掌握可化为一元二次方程或一元二次方程的分式方程的解法。 3、渗透转化思想。
学习重点 学习难点 重点:解可化为一元一次方程的分式方程. 难点:增根的概念和验根的必要性,学生较难理解。
学习过程 学教记录
【自主预学】:认真阅读课本P130至P131,回答下列问题1、已知分式 ,当x ____________时,分式有意义. 分式 与 的最简公分母是 __________. 完成课本P130页合作学习部分 回答下列问题 (1)分式方程概念:只含有_________,或分式和整式,并且分母里含有__________的方程叫做分式方程 . (2)P130做一做下列方程中,哪些是分式方程?哪些不是分式方程?为什么?【课堂导学】:活动一:解分式方程 思路:例1:解: 方程的两边同乘以最简公分母_______________ 得:化解得整式方程: 解整数方程得:检验:把 x = -9代入原方程左边= , . 左边=右边,所以___________是原方程的解。 2练一练(2) (2) (3) 活动二:增根 例2:解方程 (增根:在去分母,将分式方程转化为整式方程的过程中出现的不适合于原方程的根.既使分母为0的根。)【分层助学】: 其中分式方程有____________________. 要把分式方程化为整式方程,方程两边应同乘 ; 如果有增根,那么增根为________________.4解方程 (1) (2) (3) 【课外拓展】当为何值时,方程会产生增根?分析(1)方程的增根是___________(2 ) 原方程去分母两边同乘____________得: 把增根代入得________________,_____________. 练习:若分式方程 有增根x=2,则 a= 【课后作业】:作业本 【反思促学】:
课题 5.5分式方程(2)
主备人 集体备课时间 上课时间
复习目标 1、会列分式方程解简单应用题 2、会进行简单的公式变形
复习重点 复习难点 重点:列分式方程解简单应用题 难点:例3 是本节难点
学习过程 学教记录
【自主预学】:认真阅读课本P132至P133,回答下列问题1.甲、乙两人每时共能做35个电器零件,当甲做了90个零件时,乙做了120个,问甲、乙每时各做多少个电器零件? 分析:(1)每时做的零件数= ÷ (2)方程的等量关系: 。 (3)列出方程: 。 2.列分式方程解应用题的一般步骤: 、 、 、 、 、 3.下面的公式变形对吗?如果不对,应怎样改正? 将公式(1+ax≠0)变形成已知x,a,求b。 解:由 ,得 , ∴ ,即 。【课堂导学】: 例3 某地水稻种植基地在A、B两个面积相同的试验田里种植不同品种的水稻,分别收获16.8吨和13.2吨。已知A试验田的水稻比B试验田的水稻每公顷多收获3吨,分别求A、B两个试验田每公顷的水稻产量。 基本数量关系: 解:设 例4 照片机成像应用了一个重要原理,即。其中表示照相机镜头的焦距,表示物体到镜头的距离,表示胶片(像)到镜头的距离。如果一架照相机已固定,那么就要依靠调整、来使成像清晰。如果用焦距=35mm的相机,拍摄离镜头的距离=2m的花卉,成像清晰,那么拍摄时胶片到镜头的距离大约是多少(精确到0.1mm)? 【分层助学】:1.将下面的公式变形 (1) (用p和b 表示a)(2) (用f,v表示u) 2.工厂生产一种电子配件,每只的成本为2元,毛利率为25%,后来该工厂通过改进工艺,降低了成本,在售价不变的情况下,毛利率增加了15%,问这种配件每只的成本降低了多少元?(精确到0.01元)分析:(1)本题等量关系是: (2)售出价是: (3)成本是: (4) 根据等量关系,你能列出方程: (5)解方程: 3.某班学生到距学校12千米的烈士陵园扫墓。一部分同学骑自行车先行,经时后,其余同学乘汽车出发,结果他们同时到达。已知汽车的速度是自行车速度的3倍,求汽车和自行车的速度。 4.某市从今年1月1日起调整居民用水价格,每m3水费上涨三分之一,小丽家去年12月的水费是15元,今年2月的水费是30元.已知今年2月的用水量比去年12月的用水量多5m3,求该市今年居民用水的价格?【课外拓展】在下渚湖里划船发现逆流划行400米的时间比顺流划行400米的时间多用了5分钟。已知水流速度为20米/分,求我们在静水中划船速度. 【课后作业】: 【反思促学】:
课题 分式复习
主备人 集体备课时间 上课时间
复习目标 1.分式的概念,分式有意义的条件,分式的值为零的条件,分式的基本性质,最简分式,约分,通分。分式的乘除运算,同分母分式的加减,异分母分式的加减。2.分式方程及其应用。
复习重点 复习难点 重点:分式的混合计算 难点:分式方程的应用
学习过程 学教记录
1.下列各式中,是分式的是( ) A. B. x2 C. D. -3x+ 2.分式有意义及分式值为0时的条件 当x ________时分式无意义;当x _______时分式的值为零。 3.分式的基本性质 1、 分式中的都扩大两倍,则分式的值 。 2、(1)(b—1) (2)。 4.约分 (1) _________,(2) __________。 5.最简分式 分式中,最简分式有 ( ) A.1个 B .2个 C.3个 D.4个 6.通分(找最简公分母) 分式的最简公分母为_________________ 7.分式的乘除 (1) (2)3xy2 (3) 8.同分母分式的加减 =____________________ 9.异分母分式的加减 (1) = (2) = 10.解分式方程 (1) ; (2) 11、列分式方程解应用题某车间有甲乙两个小组,甲组的工作效率比乙组高25%,因此甲组加工2000个零件所用时间比乙组加工1800个零件所用的时间还少30分钟,求乙组每小时加工多少个零件? 分层助学: 1.当x_______时,分式有意义。 2.化简:=_______;=_______;=____________。 3.计算:(1) (2)( (3) (4) 4.先化简,再求值。( , 其中。 5.A、B两地相距80千米,甲骑车从A地出发1小时后,乙也从A地出发,用相当于甲1.5倍的速度追赶,当追赶到B地时,甲比乙先到20分钟。求甲、乙的速度。
分式方程
整式方程
解整式方程
检验
PAGE
主备人 集体备课时间 上课时间
学习目标 1、了解分式的概念. 2、了解分式有意义的条件. 3、会用分式表示简单实际问题中的数量关系.
学习重点 学习难点 重点:分式的概念 难点:例2的问题情境较为复杂,并且涉及到分式、求分式的值等问题
学习过程 学教记录
【自主预学】:认真阅读课本P114至P115,回答下列问题(1、由数与字母或字母与字母相乘组成的代数式叫做__________.由几个单项式相加组成的代数式叫做__________.单项式、多项式统称为___________.2、分数的分母不能为_________,当分母为________时,分数没有意义. 【课堂导学】:(一)根据下列条件列出代数式 1、小明家距离学校2千米,从家骑车出发以25千米/小时的速度到学校,需__ _小时.2、班级篮球赛中,某班花了400元购买了m件男式汗衫和n件女式汗衫,那么平均每件汗衫的成本价是 元. 3、在校首届辩论赛中,102班的5位同学参加了辩论,共发言x次,那么每位辩手平均发言_______次.4、在“校园之星”展出活动中,每块展板的面积为s ,长为x,则宽为________. 5、捐书活动共有a人参加,其中男生共捐b本书,女生共捐c本书,那么平均每人捐出 本书. 6、为了调查珍稀动物资源,动物专家在p平方千米的保护区内找到了7只灰熊,则该保护区内平均每平方千米内有 只灰熊。归纳:表示两个______相除,且__________中含有字母的代数式叫做分式.(二)做一做、书本第114页思考: 1、如何判断一个代数式是不是分式? 2、分式中的字母能取任何实数吗?(三)例1、已知分式. 当x取什么数时,分式有意义? 当x取什么数时,分式的值为零? 当x=1时,分式的值是多少? 变式 已知分式.当x_______时,分式无意义; 当x_______时,分式的值为零. 归纳: 1、分式有意义的条件是_____________________________. 2、分式值为零的条件是_____________________________. (四) 例2、甲﹑乙两人从一条公路的某处出发,同向而行.已知甲每时行a千米,乙每时行b千米,a>b.如果乙提前1时出发,那么甲追上乙需要多少时间?当a=6,b=5时,求甲追上乙所需要的时间? 【分层助学】:1、当x___________时,分式有意义; 2、当x_________时,分式的值为零; 3、当x_________时,分式有意义. 4、已知分式,请在-2,0,1中任意选一个你喜欢的x代入求值.【课外拓展】1、某厂的仓库里有煤p吨,每天需用煤q(q>1)吨.若从现在开始,每天节省1吨煤,则p吨煤可用多少天?当p=10,q=3时,仓库里的煤可用几天?2、已知汽车的速度为v千米/时,甲、乙两地的路程是s千米。 该汽车行驶t小时的路程是 千米,从甲地到乙地需 行驶 小时。 如果该汽车的速度加快a千米/时,那么从甲地到乙地需 行驶 小时,加快后比加快前少用 小时。 3、 要使分式 没有意义,则x的值是 。4、要使分式 取值 有意义,那么x的取值为 。 【课后作业】:作业本 【反思促学】:
课题 5.2分式基本性质(1)
主备人 集体备课时间 上课时间
学习目标 1、理解分式的基本性质. 2、会进行分式的约分.
学习重点 学习难点 重点:分式的基本性质. 难点:例1第(2)题的约分过程.
学习过程 学教记录
【自主预学】:认真阅读课本P117至P118,回答下列问题下面这些式子成立吗?依据是什么?== == 你能讲出分数的基本性质,类似地,分式也有以下基本性质:1.分式也有以下基本性质: 分式的分子与分母都乘以(或除以)同一个 的整式,分式的值不变。 2.用式子表示为 = ,= (其中M是不等于零的 ) 3.分式的约分:把一个分式的分子与分母的 约去,叫做分式的约分4.分子、分母没有公因式的分式叫做最简分式。(约分要约去分子、分母中 分因式。5、分式的符号性质:==( )=( ). 【课堂导学】:例1、化简下列分式: (1) (2) 2、不改变分式的值,把下列各式的分子与分母中的各项子数都化为整数。 (1) eq \f (x+y,x-y) (2) 2、不改变分式的值,使下列分式的分子与分母都不含“-”号.(1) ?????????????????????? (2)??????????????????? ? (3)【分层助学】:约分: (1) (2) (3) (4) 【课外拓展】 1.等式=成立的条件是 . 2.若把分式中的x和y都扩大3倍,那么分式的值( )A.扩大3倍 B.不变 C.缩小3倍 D.缩小6倍3. 下列各式中,正确的是( ) A. B. C. D. 4.约分:(1) (2) (3) (4) 【课后作业】:作业本 【反思促学】
课题 5.2分式基本性质(2)
主备人 集体备课时间 上课时间
学习目标 进一步掌握分式的基本性质及其应用. 会在已知等式的情况下将分式化简或求值,体验等量替换、整体代换的数学思想的方法. 3、会应用分式的约分进行多项式的除法。
学习重点 学习难点 重点:运用分式的约分进行多项式的除法. 难点:在已知等式的情况下将分式化简或求值.
学习过程 学教记录
【自主预学】:认真阅读课本P20至P121,回答下列问题一、复习巩固1.约分。 (1) (2) 2.已知m-3n=0,求分式的值 【课堂导学】:例2.已知 ,求分式 的值。 练一练P120课内练习1、2 例3.(1) (2) 两个多项式相除可以先表示成分式,通过因式分解、约分等把分式化简,用整式或最简分式表示商。【分层助学】:1计算 (1)(4a+a)÷(4a+1) (2)(x+2x)÷(x+2) (3)(3m+3m)÷(1-m) (4)(3xy-6xy)÷(2y-x) 2完成课本P121作业题.【课外拓展】 1.若=2,则= . 2.计算:(x-18x+81)÷(x+6x+9) 3.已知a+=2,求a+的值. 已知+=5,求的值. 【课后作业】:作业本 【反思促学】
课题 5.3分式的乘除
主备人 集体备课时间 上课时间
学习目标 1、掌握分式的乘除法则2、会进行分式的乘除运算,并会用来解决简单的实际问题。
学习重点 学习难点 重点:分式的乘除法则难点:例1 第(3)题的计算过程比较复杂,有一定的困难。
学习过程 学教记录
【自主预学】:认真阅读课本P121至P123,回答下列问题1.你能完成下列运算吗? 2、类比上面的分数乘除法运算,猜一猜 【课堂导学】:1.小组活动:(1)运算的根据是什么? (2)类比分数的乘除法法则,你能说出分式的乘除法法则吗?乘法法则:分式乘分式,用____________作为积的分子,_____________作为积的分母除法法则:分式除以分式,把_____________________________后,再与____________相乘。用式子表示为:_____________________________________________2、相信你能做对! (1) (2) (3) (4)例1:计算:(1) (2) (3) (4) 例2 一个长、宽、高分别为l,b,h的长方形纸箱装满了一层高为h的圆柱形易拉罐(如图).求纸箱空间的利用率(易拉罐总体积与纸箱容积的比,结果精确到1%). 3知识梳理:分式的乘除法运算要注意:(1) 分式的分子、分母是多项式时,一般要要先 后再进行乘法计算;。(2) 分式的乘除法运算顺序是 ;(3) 若分式与整式相乘除,应把整式看作是分母为 的式子; (4)计算的结果一定是 .【分层助学】:1、下列各式正确的是( )A. B. C. D.2、化简分式后得( )A.-a+b; B.-a-b; C.a-b; D.a+b3、计算(1) (2)【课外拓展】已知==≠0,求的值. 【课后作业】:作业本 【反思促学】:
课题 5.4分式的加减(1)
主备人 集体备课时间 上课时间
学习目标 掌握同分母分式加减的法则 会进行同分母分式的加减运算
学习重点 学习难点 重点:同分母分式的加减运算 难点:例2涉及两个分式的分母需作适当转化后才能运用同分母分式的加减法则是本节学习的难点。
学习过程 学教记录
【自主预学】:认真阅读课本P125至P126,回答下列问题1.计算: 类似地, _________,_________, 结论:同分母分式相加减,分母 ,把分子 。 2做一做 【课堂导学】:1.填空: (1) , (2) 。2、例1计算: (1) (2) 思考:这两题的中的两个分式同分母吗?3、练习(1) (2) (3) 4.完成课本P126课内练习1、2.例2先化简,再求值:其中x=3问:两个分式是否同分母?怎么化成同分母呢? 【分层助学】:1.计算:(1) , (2) , (3) , (4) 。 2、先化简,在求值:,其中m=2011,n=-1.【课外拓展】已知 (1)化简P、Q; (2)请你选择自己喜欢的一组的值,分别代入求P、Q的值; (3)比较P、Q的大小,并说明理由。 【课后作业】:作业本 【课后作业】:
课题 5.4分式的加减(2)
主备人 集体备课时间 上课时间
学习目标 学会异分母分式的通分 学会异分母分式的加减运算
学习重点 学习难点 重点:异分母分式的加减运算 难点:通分的过程是本节学习的难点。
学习过程 学教记录
【自主预学】:认真阅读课本P127至P128,回答下列问题1.先化简,再计算: ,其中x =6 。 2.计算根据异分母分数的加减法法则计算: 1)-= (2) 1--= 2) 对照上面的计算,完成下列填空:(1)+=+= (2)-=-( )= 什么叫做通分: 【课堂导学】:1.议一议:你能通过分式的通分,完成下面的填空吗? ; . 2、例3 计算: (1) (2) (3) 公分母: 公分母: 公分母: 3、例4 计算,并求当时原式的值。 【分层助学】:计算 (5) (6) 化简,并选择你喜欢的a值代入,求出原式的值。 【课外拓展】 【课后作业】: 【反思促学】
课题 5.5分式的方程(1)
主备人 集体备课时间 上课时间
学习目标 1、会根据定义判别分式方程与整式方程,了解分式方程增根产生的原因,掌握验根的方法。 2、掌握可化为一元二次方程或一元二次方程的分式方程的解法。 3、渗透转化思想。
学习重点 学习难点 重点:解可化为一元一次方程的分式方程. 难点:增根的概念和验根的必要性,学生较难理解。
学习过程 学教记录
【自主预学】:认真阅读课本P130至P131,回答下列问题1、已知分式 ,当x ____________时,分式有意义. 分式 与 的最简公分母是 __________. 完成课本P130页合作学习部分 回答下列问题 (1)分式方程概念:只含有_________,或分式和整式,并且分母里含有__________的方程叫做分式方程 . (2)P130做一做下列方程中,哪些是分式方程?哪些不是分式方程?为什么?【课堂导学】:活动一:解分式方程 思路:例1:解: 方程的两边同乘以最简公分母_______________ 得:化解得整式方程: 解整数方程得:检验:把 x = -9代入原方程左边= , . 左边=右边,所以___________是原方程的解。 2练一练(2) (2) (3) 活动二:增根 例2:解方程 (增根:在去分母,将分式方程转化为整式方程的过程中出现的不适合于原方程的根.既使分母为0的根。)【分层助学】: 其中分式方程有____________________. 要把分式方程化为整式方程,方程两边应同乘 ; 如果有增根,那么增根为________________.4解方程 (1) (2) (3) 【课外拓展】当为何值时,方程会产生增根?分析(1)方程的增根是___________(2 ) 原方程去分母两边同乘____________得: 把增根代入得________________,_____________. 练习:若分式方程 有增根x=2,则 a= 【课后作业】:作业本 【反思促学】:
课题 5.5分式方程(2)
主备人 集体备课时间 上课时间
复习目标 1、会列分式方程解简单应用题 2、会进行简单的公式变形
复习重点 复习难点 重点:列分式方程解简单应用题 难点:例3 是本节难点
学习过程 学教记录
【自主预学】:认真阅读课本P132至P133,回答下列问题1.甲、乙两人每时共能做35个电器零件,当甲做了90个零件时,乙做了120个,问甲、乙每时各做多少个电器零件? 分析:(1)每时做的零件数= ÷ (2)方程的等量关系: 。 (3)列出方程: 。 2.列分式方程解应用题的一般步骤: 、 、 、 、 、 3.下面的公式变形对吗?如果不对,应怎样改正? 将公式(1+ax≠0)变形成已知x,a,求b。 解:由 ,得 , ∴ ,即 。【课堂导学】: 例3 某地水稻种植基地在A、B两个面积相同的试验田里种植不同品种的水稻,分别收获16.8吨和13.2吨。已知A试验田的水稻比B试验田的水稻每公顷多收获3吨,分别求A、B两个试验田每公顷的水稻产量。 基本数量关系: 解:设 例4 照片机成像应用了一个重要原理,即。其中表示照相机镜头的焦距,表示物体到镜头的距离,表示胶片(像)到镜头的距离。如果一架照相机已固定,那么就要依靠调整、来使成像清晰。如果用焦距=35mm的相机,拍摄离镜头的距离=2m的花卉,成像清晰,那么拍摄时胶片到镜头的距离大约是多少(精确到0.1mm)? 【分层助学】:1.将下面的公式变形 (1) (用p和b 表示a)(2) (用f,v表示u) 2.工厂生产一种电子配件,每只的成本为2元,毛利率为25%,后来该工厂通过改进工艺,降低了成本,在售价不变的情况下,毛利率增加了15%,问这种配件每只的成本降低了多少元?(精确到0.01元)分析:(1)本题等量关系是: (2)售出价是: (3)成本是: (4) 根据等量关系,你能列出方程: (5)解方程: 3.某班学生到距学校12千米的烈士陵园扫墓。一部分同学骑自行车先行,经时后,其余同学乘汽车出发,结果他们同时到达。已知汽车的速度是自行车速度的3倍,求汽车和自行车的速度。 4.某市从今年1月1日起调整居民用水价格,每m3水费上涨三分之一,小丽家去年12月的水费是15元,今年2月的水费是30元.已知今年2月的用水量比去年12月的用水量多5m3,求该市今年居民用水的价格?【课外拓展】在下渚湖里划船发现逆流划行400米的时间比顺流划行400米的时间多用了5分钟。已知水流速度为20米/分,求我们在静水中划船速度. 【课后作业】: 【反思促学】:
课题 分式复习
主备人 集体备课时间 上课时间
复习目标 1.分式的概念,分式有意义的条件,分式的值为零的条件,分式的基本性质,最简分式,约分,通分。分式的乘除运算,同分母分式的加减,异分母分式的加减。2.分式方程及其应用。
复习重点 复习难点 重点:分式的混合计算 难点:分式方程的应用
学习过程 学教记录
1.下列各式中,是分式的是( ) A. B. x2 C. D. -3x+ 2.分式有意义及分式值为0时的条件 当x ________时分式无意义;当x _______时分式的值为零。 3.分式的基本性质 1、 分式中的都扩大两倍,则分式的值 。 2、(1)(b—1) (2)。 4.约分 (1) _________,(2) __________。 5.最简分式 分式中,最简分式有 ( ) A.1个 B .2个 C.3个 D.4个 6.通分(找最简公分母) 分式的最简公分母为_________________ 7.分式的乘除 (1) (2)3xy2 (3) 8.同分母分式的加减 =____________________ 9.异分母分式的加减 (1) = (2) = 10.解分式方程 (1) ; (2) 11、列分式方程解应用题某车间有甲乙两个小组,甲组的工作效率比乙组高25%,因此甲组加工2000个零件所用时间比乙组加工1800个零件所用的时间还少30分钟,求乙组每小时加工多少个零件? 分层助学: 1.当x_______时,分式有意义。 2.化简:=_______;=_______;=____________。 3.计算:(1) (2)( (3) (4) 4.先化简,再求值。( , 其中。 5.A、B两地相距80千米,甲骑车从A地出发1小时后,乙也从A地出发,用相当于甲1.5倍的速度追赶,当追赶到B地时,甲比乙先到20分钟。求甲、乙的速度。
分式方程
整式方程
解整式方程
检验
PAGE
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
