6.4频数与频率(2) 同步训练(含解析)
文档属性
| 名称 | 6.4频数与频率(2) 同步训练(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-30 08:51:15 | ||
图片预览


文档简介
初中数学浙教版七年级下册6.4频数与频率(2) 同步训练
一、单选题
1.王老师对本班40名学生的血型作了统计,列出如下统计表,则本班A型血的人数是(? ?). 2·1·c·n·j·y
A.?16人?????????????????????????????????????B.?14人?????????????????????????????????????C.?4人?????????????????????????????????????D.?6人
2.陈老师对56名同学的跳绳成绩进行了统计,跳绳个数140个以上的有28名同学,则跳绳个数140个以上的频率为(??? ) 2-1-c-n-j-y
A.?0.4?????????????????????????????????????????B.?0.2?????????????????????????????????????????C.?0.5?????????????????????????????????????????D.?2
3.为了了解某校初三年级学生的运算能力,抽取了100名学生进行测试,将所得成绩(单位:分)整理后,列出下表: 21世纪教育网版权所有
分组
50~59
60~69
70~79
80~89
90~99
频率
0.06
0.16
0.08
0.30
0.40
本次测试这100名学生成绩良好(大于或等于80分为良好)的人数是(??? )
A.?22?????????????????????????????????????????B.?30?????????????????????????????????????????C.?60?????????????????????????????????????????D.?70
4.调查50名学生的年龄,列频数分布表时,这些学生的年龄落在5个小组中,第一、二、三、五组数据个数分别是2,8,15,5,则第四组的频数是( ??) 21*cnjy*com
A.?20????????????????????????????????????????B.?30????????????????????????????????????????C.?0.4????????????????????????????????????????D.?0.6
5.某校为了了解九年级学生的体能情况,随机抽查了其中的30名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的须数分布直方图.根据图示计算,仰卧起坐次数在15-20次之间的频率是(??? )
A.?0.1??????????????????????????????????????B.?0.17??????????????????????????????????????C.?0.33??????????????????????????????????????D.?0.4
6.某单位有职工100名,按他们的年龄分成8组,在40~42(岁)组内有职工32名,那么这个小组的频率是(??? ) 21·世纪*教育网
A.?0.12??????????????????????????????????????B.?0.38??????????????????????????????????????C.?0.32??????????????????????????????????????D.?32
7.2018年11月贵阳市教育局对某校七年级学生进行体质监测共收集了200名学生的体重,并绘制成了频数分布直方图,从左往右数每个小长方形的长度之比为2:3:4:1,其中第三组的频数为(??? )
A.?? 80人???????????????????????????????????B.?60人???????????????????????????????????C.?20人???????????????????????????????????D.?10人
8.某校数学教研组有25名教师,将他们的年龄分成3组,在38~45(岁)组内有8名教师,那么这个小组的频率是(? ?).
A.?0.12?????????????????????????????????????B.?0.38?????????????????????????????????????C.?0.32?????????????????????????????????????D.?3.12
9.已知数据10,9,8,7,6,6,9,10,7,9,6,7,10,9,6,8,9,10,6,9那么频率为0.5的范围是(?? )
A.?5.5~7.5????????????????????????????B.?6.5~8.5????????????????????????????C.?7.5~9.5????????????????????????????D.?8.5~10.5
二、填空题
10.对1850个数据进行整理.在频数的统计表中,各组的频率之和等于________.
11.在一样本容量为80的样本中,已知某组数据的频率为0.7,频数为________.
12.某校对1200名女生的身高进行了测量,其中身高在1.58~1.63(单位:cm )的这一小组的频率为0.25,则该组的人数为________人
13.在样本容量为200的频数直方图中,共有3个小长方形,若第一个长方形对应的频率为10%,若中间一个小长方形的高与其余两个小长方形高的和之比是2:3,则中间一组的频率为________.
14.秋季新学期开学时,某中学对六年级新生掌握“中学生日常行为规范”的情况进行了知识测试,测试成绩全部合格,现学校随机选取了部分学生的成绩,整理并制作成了不完整的图表(如表所示),图表中c=________.
分 数 段
频数
频率
60≤x<70
6
a
70≤x<80
20
0.4
80≤x<90
15
b
90≤x≤100
c
0.18
三、综合题
15.为了解某校八年级学生每天干家务活的平均时间,小颖同学在该校八年级每班随机调查5名学生,统计这些学生2014年3月每天干家务活的平均时间(单位:min),绘制成如下统计表(其中A表示0~10min;B表示11~20min;C表示21~30min;时间取整数):
干家务活平均时间
频数
百分比
A
10
25%
B
a
62.5%
C
5
b
合计
c
1
(1)统计表中的a=________;b=12.5%;c=________;
(2)该校八年级共有240名学生,其中大约有________名学生每天干家务活的平均时间是11~20min.
16.某学校为了解本校九年级学生期末考试数学成续情况,决定进行抽样分析,已知该校九年级共有10个班,每班40名学生,请根据要求回答下列问题:
(1)若要从全年级学生中抽取一个40人的样本,你认为以下抽样方法中比较合理的有________.(只要填写序号)
①随机抽取一个班级的学生;②在全年级学生中随机抽取40名男学生:③在全年级10个班中各随机抽取4名学生.21·cn·jy·com
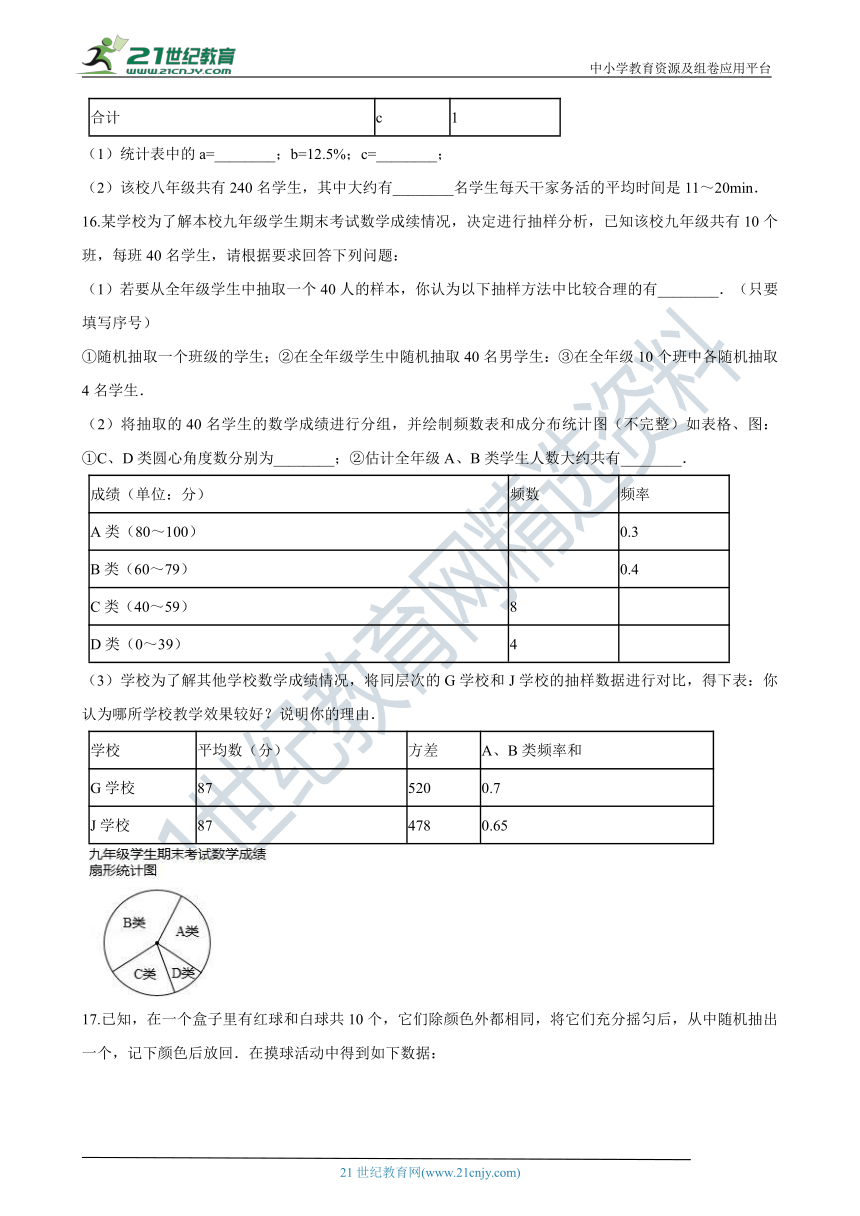
(2)将抽取的40名学生的数学成绩进行分组,并绘制频数表和成分布统计图(不完整)如表格、图:①C、D类圆心角度数分别为________;②估计全年级A、B类学生人数大约共有________.
成绩(单位:分)
频数
频率
A类(80~100)
0.3
B类(60~79)
0.4
C类(40~59)
8
D类(0~39)
4
(3)学校为了解其他学校数学成绩情况,将同层次的G学校和J学校的抽样数据进行对比,得下表:你认为哪所学校教学效果较好?说明你的理由.
学校
平均数(分)
方差
A、B类频率和
G学校
87
520
0.7
J学校
87
478
0.65
17.已知,在一个盒子里有红球和白球共10个,它们除颜色外都相同,将它们充分摇匀后,从中随机抽出一个,记下颜色后放回.在摸球活动中得到如下数据:
摸球总次数
50
100
150
200
250
300
350
400
450
500
摸到红球的频数
17
32
44
64
78
??
103
122
136
148
摸到红球的频率
0.34
0.32
0.293
0.32
0.312
0.32
0.294
??
0.302
??
(1)请将表格中的数据补齐;
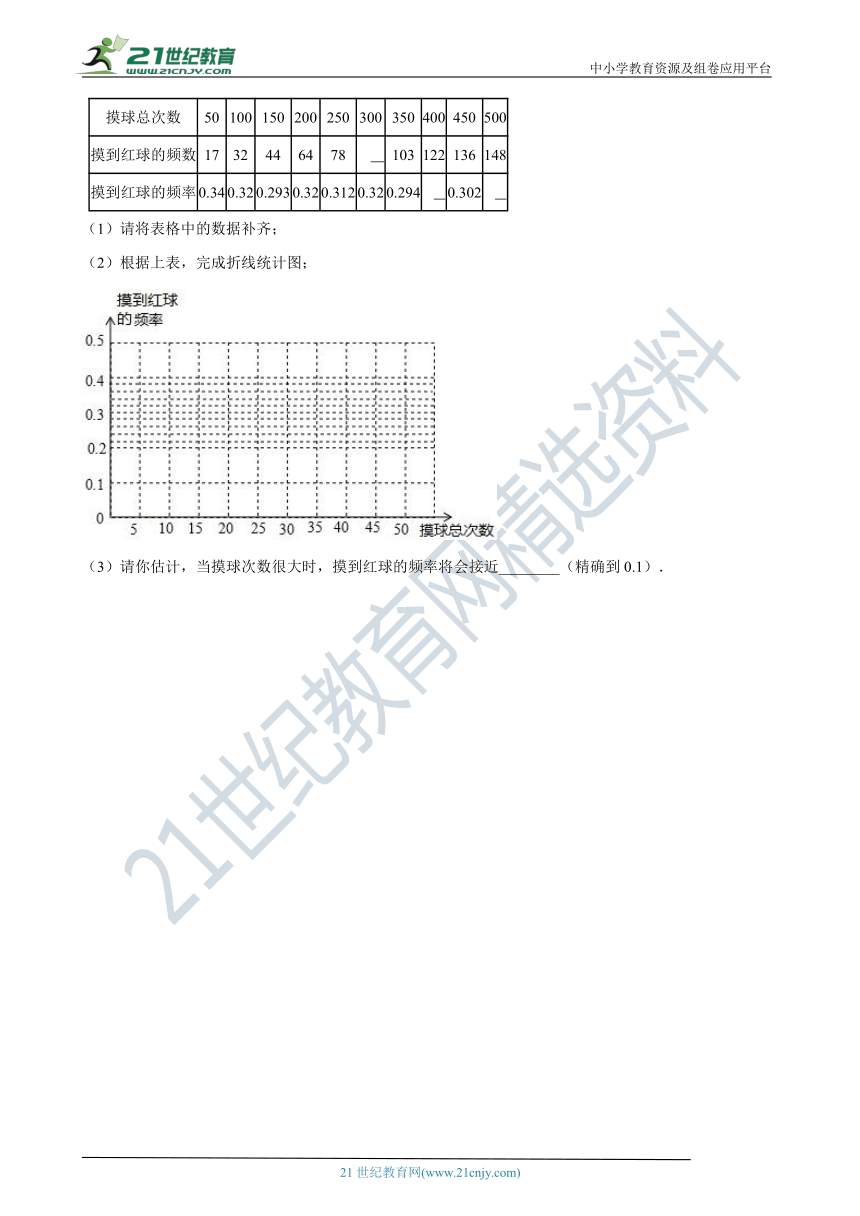
(2)根据上表,完成折线统计图;
(3)请你估计,当摸球次数很大时,摸到红球的频率将会接近________(精确到0.1).
答案解析部分
一、单选题
1. A
解:本班A型血的人数为:40÷0.4=16人. 故答案为:A.
【分析】根据频数=数据总数×频率,列式计算即可。
2. C
解:由题意得 28÷56=0.5. 故答案为:C 【分析】利用频率=频数÷总数,列式计算。21cnjy.com
3. D
解:?解:成绩良好的人数=100×(0.3+0.4)=70, 故答案为:D. 【分析】根据”成绩良好的人数=抽取的学生人数×成绩良好的频率“计算即可得出结果。
4. A
解:第四组的人数为:50-(2+8+15+5)=20, 即第四组的频数为20; 故答案为:20. 【分析】先根据抽查的人数减去四组已知的人数计算得出第五组的人数,即可得出第四组的频率。
5. A
解:仰卧起坐次数在15~20次的频率为:3/30 =0.1
故答案为:A
【分析】先根据直方图中的信息,把各小组的频数相加可得样本容量,根据频率=频数÷样本容量即可求解。
6. C
解:∵ 某单位有职工100名,在40~42(岁)组内有职工32名, ∴这个小组的频率为:32÷100=0.32 故答案为:C 【来源:21·世纪·教育·网】
【分析】利用频率=频数÷总数,列式计算可求解。
7. A
解:200× =80,
即第三组的频数为80,
故答案为:A.
【分析】先计算出第三组的频率,然后用利用频数=总数×频率计算即得。
8. C
解:∵某校数学教研组有25名教师,将他们的年龄分成3组,在38~45(岁)组内有8名教师, ∴这个小组的频率=8÷25=0.32. 故答案为:C. www-2-1-cnjy-com
【分析】根据频率的求法:频率=频数÷数据总和,列式计算即可.
9. D
解:对于A选项,5.5-7.5的频数为8,频率=8÷20=0.4<0.5,故A选项不符合题意;
对于B选项,6.5-8.5的频数为5,频率=5÷20=0.25<0.5,故B选项不符合题意;
对于C选项,7.5-9.5的频数为8,频率=8÷20=0.4<0.5,故C选项不符合题意;
对于D选项,8.5-10.5的频数为10,频率=10÷20=0.5,故D选项符合题意.
故答案为:D.
【分析】根据“频率=频数÷数据的总数”,已知数据的总数,只需求出各组频数即可;接下来根据各选项中所给的范围求出各组数据的频数,再对0.5进行比较即可.【来源:21cnj*y.co*m】
二、填空题
10. 1
解:对1850个数据进行整理.在频数的统计表中,各组的频数之和为1850, ∴各组的频率之和为1. 故答案为:1. 【分析】由题意可知各组的频数之和为1850,则可得到频率之和为1。【出处:21教育名师】
11. 56
解:样本容量为80,某组样本的频率为0.7,该组样本的频数=0.7×80=56。
故答案为:56。
【分析】用样本容量乘以该组数据的频率即可算出该组数据的频数。
12. 300
解:由题意得: 1200×0.25=300. 故答案为:300.
【分析】利用频数=总数×频率,列式计算。
13. 0.4
解:∵中间一个小长方形的高与其余两个小长方形高的和之比是2:3 ∴中间一组的频率为:. 故答案为:0.4. 【分析】根据长方形的高之比就是频率的比,即可求出中间一组的频率。【版权所有:21教育】
14. 9
解:20÷0.4=50,c=50×0.18=9。 故答案为:9。 【分析】由频率=, 可根据分数段在70≤x≤80的频数、频率求出总数,接着可求出c。
三、综合题
15.(1)25;40 (2)150
解:(1)根据题意得:
c= =40,则a=40×62.5%=25;
?b= ×100%=12.5%;
故答案为:25;12.5%;40
( 2 )根据题意得:240×62.5%=150(名),
答:大约有150名学生每天干家务活的平均时间是11~20min
【分析】(1)总数=频数÷频率,即c=10÷25%=40;(2)八年级的总人数乘以每天干家务活的平均时间为11~20min的学生所占的百分比,即可得到答案。www.21-cn-jy.com
16. (1)③ (2)72°、36°;280人 (3)解:G学校教学效果较好,
理由:因为A、B两类频率之和G学校大于J学校,即相对高分人数G学校多于J学校,所以G学校教学效果较好.21教育名师原创作品
解:(1)由题意可得,
若要从全年级学生中抽取一个40人的样本,在全年级10个班中各随机抽取4名学生比较合理,
故答案为:③;
( 2 )①C类圆心角度数为:360°× =72°,D类圆心角度数为:360°× =36°,
故答案为:72°、36°;
②估计全年级A、B类学生人数大约共有:400×(0.3+0.4)=280(人),
故答案为:280人;
【分析】(1)根据抽样调查所选取的样本必须具有代表性及全面性,即可得出答案; (2)用360°乘以C类学生的频率即可求出C类圆心角度数;同理算出D类圆心角度数;用全校的学生总人数400乘以A,B两类学生的频率和即可估计全年级A、B类学生人数; (3)根据两个学校的A,B类频率和即可得出判断。21*cnjy*com
17. (1)解:300×0.32=96, , ,
故答案为:96;0.305;0.296
(2)解:折线统计图如图所示:
(3)0.3
解:(3)当摸球次数很大时,摸到红球的频率将会接近0.3. 【分析】(1)根据百分数=频数样本容量即可求解; (2)根据(1)表格中的信息即可画出折线统计图; (3)根据(1)表格中的信息可知,摸到红球的频率始终在0.3左右浮动,所以摸到红球的频率将会接近0.3。
一、单选题
1.王老师对本班40名学生的血型作了统计,列出如下统计表,则本班A型血的人数是(? ?). 2·1·c·n·j·y
A.?16人?????????????????????????????????????B.?14人?????????????????????????????????????C.?4人?????????????????????????????????????D.?6人
2.陈老师对56名同学的跳绳成绩进行了统计,跳绳个数140个以上的有28名同学,则跳绳个数140个以上的频率为(??? ) 2-1-c-n-j-y
A.?0.4?????????????????????????????????????????B.?0.2?????????????????????????????????????????C.?0.5?????????????????????????????????????????D.?2
3.为了了解某校初三年级学生的运算能力,抽取了100名学生进行测试,将所得成绩(单位:分)整理后,列出下表: 21世纪教育网版权所有
分组
50~59
60~69
70~79
80~89
90~99
频率
0.06
0.16
0.08
0.30
0.40
本次测试这100名学生成绩良好(大于或等于80分为良好)的人数是(??? )
A.?22?????????????????????????????????????????B.?30?????????????????????????????????????????C.?60?????????????????????????????????????????D.?70
4.调查50名学生的年龄,列频数分布表时,这些学生的年龄落在5个小组中,第一、二、三、五组数据个数分别是2,8,15,5,则第四组的频数是( ??) 21*cnjy*com
A.?20????????????????????????????????????????B.?30????????????????????????????????????????C.?0.4????????????????????????????????????????D.?0.6
5.某校为了了解九年级学生的体能情况,随机抽查了其中的30名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的须数分布直方图.根据图示计算,仰卧起坐次数在15-20次之间的频率是(??? )
A.?0.1??????????????????????????????????????B.?0.17??????????????????????????????????????C.?0.33??????????????????????????????????????D.?0.4
6.某单位有职工100名,按他们的年龄分成8组,在40~42(岁)组内有职工32名,那么这个小组的频率是(??? ) 21·世纪*教育网
A.?0.12??????????????????????????????????????B.?0.38??????????????????????????????????????C.?0.32??????????????????????????????????????D.?32
7.2018年11月贵阳市教育局对某校七年级学生进行体质监测共收集了200名学生的体重,并绘制成了频数分布直方图,从左往右数每个小长方形的长度之比为2:3:4:1,其中第三组的频数为(??? )
A.?? 80人???????????????????????????????????B.?60人???????????????????????????????????C.?20人???????????????????????????????????D.?10人
8.某校数学教研组有25名教师,将他们的年龄分成3组,在38~45(岁)组内有8名教师,那么这个小组的频率是(? ?).
A.?0.12?????????????????????????????????????B.?0.38?????????????????????????????????????C.?0.32?????????????????????????????????????D.?3.12
9.已知数据10,9,8,7,6,6,9,10,7,9,6,7,10,9,6,8,9,10,6,9那么频率为0.5的范围是(?? )
A.?5.5~7.5????????????????????????????B.?6.5~8.5????????????????????????????C.?7.5~9.5????????????????????????????D.?8.5~10.5
二、填空题
10.对1850个数据进行整理.在频数的统计表中,各组的频率之和等于________.
11.在一样本容量为80的样本中,已知某组数据的频率为0.7,频数为________.
12.某校对1200名女生的身高进行了测量,其中身高在1.58~1.63(单位:cm )的这一小组的频率为0.25,则该组的人数为________人
13.在样本容量为200的频数直方图中,共有3个小长方形,若第一个长方形对应的频率为10%,若中间一个小长方形的高与其余两个小长方形高的和之比是2:3,则中间一组的频率为________.
14.秋季新学期开学时,某中学对六年级新生掌握“中学生日常行为规范”的情况进行了知识测试,测试成绩全部合格,现学校随机选取了部分学生的成绩,整理并制作成了不完整的图表(如表所示),图表中c=________.
分 数 段
频数
频率
60≤x<70
6
a
70≤x<80
20
0.4
80≤x<90
15
b
90≤x≤100
c
0.18
三、综合题
15.为了解某校八年级学生每天干家务活的平均时间,小颖同学在该校八年级每班随机调查5名学生,统计这些学生2014年3月每天干家务活的平均时间(单位:min),绘制成如下统计表(其中A表示0~10min;B表示11~20min;C表示21~30min;时间取整数):
干家务活平均时间
频数
百分比
A
10
25%
B
a
62.5%
C
5
b
合计
c
1
(1)统计表中的a=________;b=12.5%;c=________;
(2)该校八年级共有240名学生,其中大约有________名学生每天干家务活的平均时间是11~20min.
16.某学校为了解本校九年级学生期末考试数学成续情况,决定进行抽样分析,已知该校九年级共有10个班,每班40名学生,请根据要求回答下列问题:
(1)若要从全年级学生中抽取一个40人的样本,你认为以下抽样方法中比较合理的有________.(只要填写序号)
①随机抽取一个班级的学生;②在全年级学生中随机抽取40名男学生:③在全年级10个班中各随机抽取4名学生.21·cn·jy·com
(2)将抽取的40名学生的数学成绩进行分组,并绘制频数表和成分布统计图(不完整)如表格、图:①C、D类圆心角度数分别为________;②估计全年级A、B类学生人数大约共有________.
成绩(单位:分)
频数
频率
A类(80~100)
0.3
B类(60~79)
0.4
C类(40~59)
8
D类(0~39)
4
(3)学校为了解其他学校数学成绩情况,将同层次的G学校和J学校的抽样数据进行对比,得下表:你认为哪所学校教学效果较好?说明你的理由.
学校
平均数(分)
方差
A、B类频率和
G学校
87
520
0.7
J学校
87
478
0.65
17.已知,在一个盒子里有红球和白球共10个,它们除颜色外都相同,将它们充分摇匀后,从中随机抽出一个,记下颜色后放回.在摸球活动中得到如下数据:
摸球总次数
50
100
150
200
250
300
350
400
450
500
摸到红球的频数
17
32
44
64
78
??
103
122
136
148
摸到红球的频率
0.34
0.32
0.293
0.32
0.312
0.32
0.294
??
0.302
??
(1)请将表格中的数据补齐;
(2)根据上表,完成折线统计图;
(3)请你估计,当摸球次数很大时,摸到红球的频率将会接近________(精确到0.1).
答案解析部分
一、单选题
1. A
解:本班A型血的人数为:40÷0.4=16人. 故答案为:A.
【分析】根据频数=数据总数×频率,列式计算即可。
2. C
解:由题意得 28÷56=0.5. 故答案为:C 【分析】利用频率=频数÷总数,列式计算。21cnjy.com
3. D
解:?解:成绩良好的人数=100×(0.3+0.4)=70, 故答案为:D. 【分析】根据”成绩良好的人数=抽取的学生人数×成绩良好的频率“计算即可得出结果。
4. A
解:第四组的人数为:50-(2+8+15+5)=20, 即第四组的频数为20; 故答案为:20. 【分析】先根据抽查的人数减去四组已知的人数计算得出第五组的人数,即可得出第四组的频率。
5. A
解:仰卧起坐次数在15~20次的频率为:3/30 =0.1
故答案为:A
【分析】先根据直方图中的信息,把各小组的频数相加可得样本容量,根据频率=频数÷样本容量即可求解。
6. C
解:∵ 某单位有职工100名,在40~42(岁)组内有职工32名, ∴这个小组的频率为:32÷100=0.32 故答案为:C 【来源:21·世纪·教育·网】
【分析】利用频率=频数÷总数,列式计算可求解。
7. A
解:200× =80,
即第三组的频数为80,
故答案为:A.
【分析】先计算出第三组的频率,然后用利用频数=总数×频率计算即得。
8. C
解:∵某校数学教研组有25名教师,将他们的年龄分成3组,在38~45(岁)组内有8名教师, ∴这个小组的频率=8÷25=0.32. 故答案为:C. www-2-1-cnjy-com
【分析】根据频率的求法:频率=频数÷数据总和,列式计算即可.
9. D
解:对于A选项,5.5-7.5的频数为8,频率=8÷20=0.4<0.5,故A选项不符合题意;
对于B选项,6.5-8.5的频数为5,频率=5÷20=0.25<0.5,故B选项不符合题意;
对于C选项,7.5-9.5的频数为8,频率=8÷20=0.4<0.5,故C选项不符合题意;
对于D选项,8.5-10.5的频数为10,频率=10÷20=0.5,故D选项符合题意.
故答案为:D.
【分析】根据“频率=频数÷数据的总数”,已知数据的总数,只需求出各组频数即可;接下来根据各选项中所给的范围求出各组数据的频数,再对0.5进行比较即可.【来源:21cnj*y.co*m】
二、填空题
10. 1
解:对1850个数据进行整理.在频数的统计表中,各组的频数之和为1850, ∴各组的频率之和为1. 故答案为:1. 【分析】由题意可知各组的频数之和为1850,则可得到频率之和为1。【出处:21教育名师】
11. 56
解:样本容量为80,某组样本的频率为0.7,该组样本的频数=0.7×80=56。
故答案为:56。
【分析】用样本容量乘以该组数据的频率即可算出该组数据的频数。
12. 300
解:由题意得: 1200×0.25=300. 故答案为:300.
【分析】利用频数=总数×频率,列式计算。
13. 0.4
解:∵中间一个小长方形的高与其余两个小长方形高的和之比是2:3 ∴中间一组的频率为:. 故答案为:0.4. 【分析】根据长方形的高之比就是频率的比,即可求出中间一组的频率。【版权所有:21教育】
14. 9
解:20÷0.4=50,c=50×0.18=9。 故答案为:9。 【分析】由频率=, 可根据分数段在70≤x≤80的频数、频率求出总数,接着可求出c。
三、综合题
15.(1)25;40 (2)150
解:(1)根据题意得:
c= =40,则a=40×62.5%=25;
?b= ×100%=12.5%;
故答案为:25;12.5%;40
( 2 )根据题意得:240×62.5%=150(名),
答:大约有150名学生每天干家务活的平均时间是11~20min
【分析】(1)总数=频数÷频率,即c=10÷25%=40;(2)八年级的总人数乘以每天干家务活的平均时间为11~20min的学生所占的百分比,即可得到答案。www.21-cn-jy.com
16. (1)③ (2)72°、36°;280人 (3)解:G学校教学效果较好,
理由:因为A、B两类频率之和G学校大于J学校,即相对高分人数G学校多于J学校,所以G学校教学效果较好.21教育名师原创作品
解:(1)由题意可得,
若要从全年级学生中抽取一个40人的样本,在全年级10个班中各随机抽取4名学生比较合理,
故答案为:③;
( 2 )①C类圆心角度数为:360°× =72°,D类圆心角度数为:360°× =36°,
故答案为:72°、36°;
②估计全年级A、B类学生人数大约共有:400×(0.3+0.4)=280(人),
故答案为:280人;
【分析】(1)根据抽样调查所选取的样本必须具有代表性及全面性,即可得出答案; (2)用360°乘以C类学生的频率即可求出C类圆心角度数;同理算出D类圆心角度数;用全校的学生总人数400乘以A,B两类学生的频率和即可估计全年级A、B类学生人数; (3)根据两个学校的A,B类频率和即可得出判断。21*cnjy*com
17. (1)解:300×0.32=96, , ,
故答案为:96;0.305;0.296
(2)解:折线统计图如图所示:
(3)0.3
解:(3)当摸球次数很大时,摸到红球的频率将会接近0.3. 【分析】(1)根据百分数=频数样本容量即可求解; (2)根据(1)表格中的信息即可画出折线统计图; (3)根据(1)表格中的信息可知,摸到红球的频率始终在0.3左右浮动,所以摸到红球的频率将会接近0.3。
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
