5.7整式的除法
图片预览






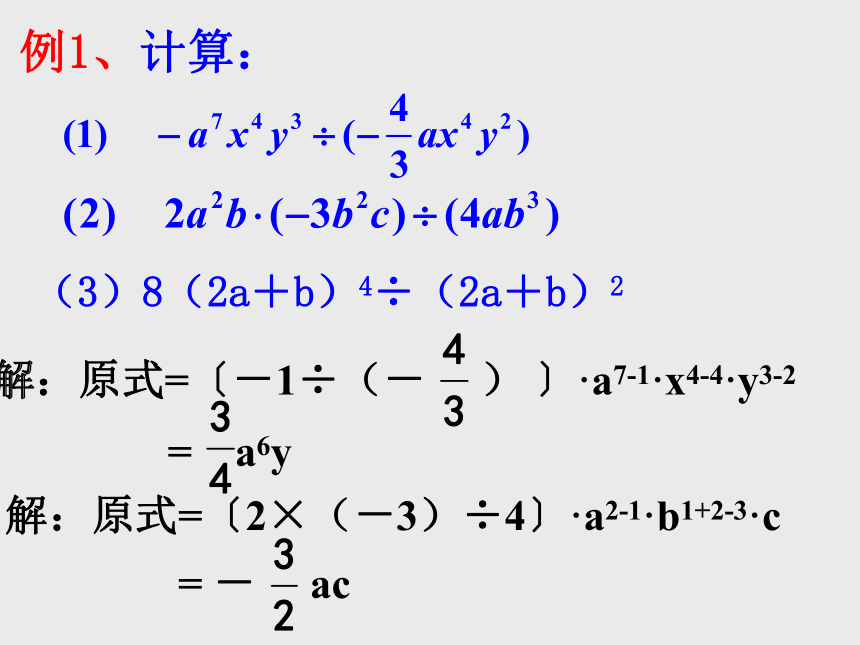

文档简介
(共27张PPT)
1.用字母表示幂的运算性质:
2.计算:
温故知新:
“阿波罗-11”号
宇航员在月球上
月球是距离地球最近的天体,它与地球的平均距
离约为 米。如果宇宙飞船以
米/秒的速度飞行,到达月球大约需要多少时间?
合作学习:
月球是距离地球最近的天体,它与地球的平均距
离约为 米。如果宇宙飞船以
米/秒的速度飞行,到达月球大约需要多少时间?
合作学习:
观察 & 归纳
仔细观察一下,并分析与思考下列几点:
(被除式的系数)÷ (除式的系数)
写在商里面作因式。
(被除式的指数) —(除式的指数)
商式的系数=
单项式除以单项式,其结果(商式)仍是
被除式里单独有的幂,
(同底数幂) 商的指数=
一个单项式;
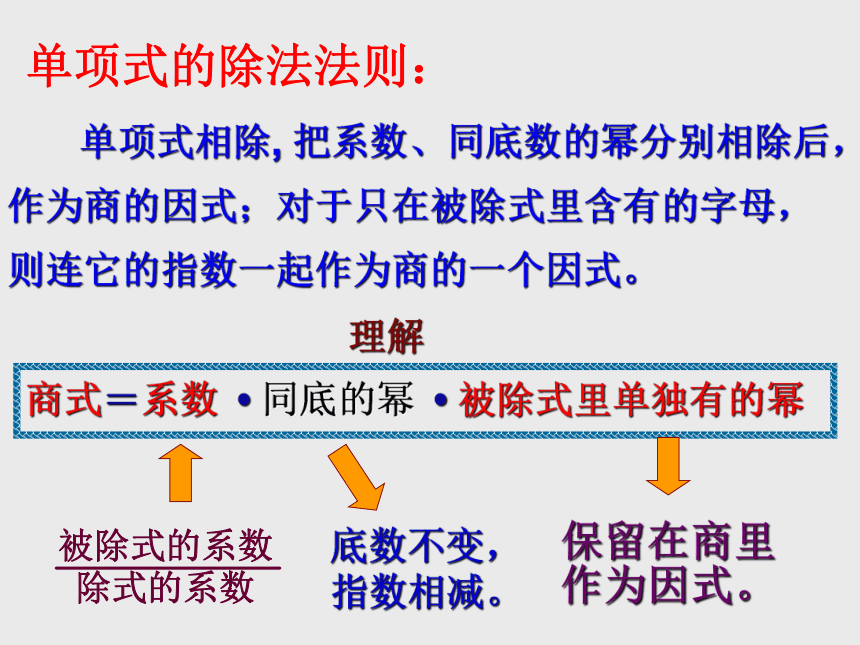
理解
商式=系数 同底的幂 被除式里单独有的幂
底数不变,
指数相减。
保留在商里
作为因式。
单项式的除法法则:
单项式相除, 把系数、同底数的幂分别相除后,作为商的因式;对于只在被除式里含有的字母,则连它的指数一起作为商的一个因式。
例1、计算:
(3)8(2a+b)4÷(2a+b)2
解:原式=〔-1÷(- ) 〕·a7-1·x4-4·y3-2
= a6y
解:原式=〔2×(-3)÷4〕·a2-1·b1+2-3·c
= - ac
练一练:
1、计算
2、下列计算错在哪里 应怎样改正
错
错
×
×
×
×
(3)4a8 ÷2a 2= 2a 4 ( )
(4)10a3 ÷5a2=5a ( )
(5)(-9x5) ÷(-3x) =-3x4 ( )
(6)12a3b ÷4a2=3a ( )
系数相除
同底数幂的除法,底数不变,指数相减
只在一个被除式里含有的字母,要连同它的指数写在商里,防止遗漏.
求系数的商,应注意符号
3、填一填:
(1)3a2÷(6a6)·(-2a4)=( )
(2)( )·3ab2=-9ab5
(3)(-12a3bc)÷( )=4a2b
-1
-3b3
-3ac
(4)
(5)-a5x3y÷(-4ax2y)
(6)2a2b(-3b2c3) ÷4a3b2
4、看谁算得既快又对:
(7)7a8b3c6 ÷(2a3b2)2.(-4a2bc)3
(1) –12a5b3c÷(–4a2b)=
(2)(–5a2b)2÷5a3b2 =
(3)4(a+b)7 ÷ (a+b)3 =
2
1
(4)(–3ab2c)3÷(–3ab2c)2 =
3a3b2c
5a
8(a+b)4
–3ab2c
做一做:
比一比,看谁最聪明:
(1)(ad+bd)÷d=__________
(2)(a2b+3ab)÷a=_________
(3)(xy3-2xy)÷(xy)=_______
a+b
ab+3b
y2-2
你对以上的解题过程中发现了什么吗?
多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加。
你能总结多项式除以单项式的法则吗
多项式除以单项式的法则:
例2、计算
1、计算
练一练:
(3)(-4a3b2+8ab3)÷(4ab2)
(4)(5x3-2x2+6x) ÷3x
(5)(2x2y3).(-7xy2) ÷(14x4y3)
(6) 3a+4
(7)
(8)
(9)
2、下列错在哪里?应怎样改正?
3、填一填:
(4) (4c3 d4- ) ÷(-3c2d)
1、系数相除;
2、同底数幂相除;
3、只在被除式里的幂不变。
先把这个多项式的每一项分别除以单项式,
再把所得的商相加。
本节课你的收获是什么?
单项式相除
多项式除以单项式
m
m
(3)
( )
=1
(2)
2
(1)
多项式
它除以 ,其商式应是( )项式,
商式为
一共有( )项
拓展练习:
(4) 计算:
3、任意给一个非零数,按下列程序计算下去,写出输出结果
= m
输入m
平方
+m
-1
输出
÷m
1.用字母表示幂的运算性质:
2.计算:
温故知新:
“阿波罗-11”号
宇航员在月球上
月球是距离地球最近的天体,它与地球的平均距
离约为 米。如果宇宙飞船以
米/秒的速度飞行,到达月球大约需要多少时间?
合作学习:
月球是距离地球最近的天体,它与地球的平均距
离约为 米。如果宇宙飞船以
米/秒的速度飞行,到达月球大约需要多少时间?
合作学习:
观察 & 归纳
仔细观察一下,并分析与思考下列几点:
(被除式的系数)÷ (除式的系数)
写在商里面作因式。
(被除式的指数) —(除式的指数)
商式的系数=
单项式除以单项式,其结果(商式)仍是
被除式里单独有的幂,
(同底数幂) 商的指数=
一个单项式;
理解
商式=系数 同底的幂 被除式里单独有的幂
底数不变,
指数相减。
保留在商里
作为因式。
单项式的除法法则:
单项式相除, 把系数、同底数的幂分别相除后,作为商的因式;对于只在被除式里含有的字母,则连它的指数一起作为商的一个因式。
例1、计算:
(3)8(2a+b)4÷(2a+b)2
解:原式=〔-1÷(- ) 〕·a7-1·x4-4·y3-2
= a6y
解:原式=〔2×(-3)÷4〕·a2-1·b1+2-3·c
= - ac
练一练:
1、计算
2、下列计算错在哪里 应怎样改正
错
错
×
×
×
×
(3)4a8 ÷2a 2= 2a 4 ( )
(4)10a3 ÷5a2=5a ( )
(5)(-9x5) ÷(-3x) =-3x4 ( )
(6)12a3b ÷4a2=3a ( )
系数相除
同底数幂的除法,底数不变,指数相减
只在一个被除式里含有的字母,要连同它的指数写在商里,防止遗漏.
求系数的商,应注意符号
3、填一填:
(1)3a2÷(6a6)·(-2a4)=( )
(2)( )·3ab2=-9ab5
(3)(-12a3bc)÷( )=4a2b
-1
-3b3
-3ac
(4)
(5)-a5x3y÷(-4ax2y)
(6)2a2b(-3b2c3) ÷4a3b2
4、看谁算得既快又对:
(7)7a8b3c6 ÷(2a3b2)2.(-4a2bc)3
(1) –12a5b3c÷(–4a2b)=
(2)(–5a2b)2÷5a3b2 =
(3)4(a+b)7 ÷ (a+b)3 =
2
1
(4)(–3ab2c)3÷(–3ab2c)2 =
3a3b2c
5a
8(a+b)4
–3ab2c
做一做:
比一比,看谁最聪明:
(1)(ad+bd)÷d=__________
(2)(a2b+3ab)÷a=_________
(3)(xy3-2xy)÷(xy)=_______
a+b
ab+3b
y2-2
你对以上的解题过程中发现了什么吗?
多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加。
你能总结多项式除以单项式的法则吗
多项式除以单项式的法则:
例2、计算
1、计算
练一练:
(3)(-4a3b2+8ab3)÷(4ab2)
(4)(5x3-2x2+6x) ÷3x
(5)(2x2y3).(-7xy2) ÷(14x4y3)
(6) 3a+4
(7)
(8)
(9)
2、下列错在哪里?应怎样改正?
3、填一填:
(4) (4c3 d4- ) ÷(-3c2d)
1、系数相除;
2、同底数幂相除;
3、只在被除式里的幂不变。
先把这个多项式的每一项分别除以单项式,
再把所得的商相加。
本节课你的收获是什么?
单项式相除
多项式除以单项式
m
m
(3)
( )
=1
(2)
2
(1)
多项式
它除以 ,其商式应是( )项式,
商式为
一共有( )项
拓展练习:
(4) 计算:
3、任意给一个非零数,按下列程序计算下去,写出输出结果
= m
输入m
平方
+m
-1
输出
÷m
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
