6.2提取公因式

(共18张PPT)
6.2
心系灾情，凝情聚爱。某校也举行赈灾献爱心活动，初一年级和初二年级均有14个班，其中初一年级平均每班捐款958元，初二年级平均每班捐款1042元，问初一、初二年级共捐款多少元？请列出式子。
14×958+14×1042
14×（958+1042）

=
1.公因式:
一般地,一个多项式中每一项都含有的相同的因式.叫做这个多项式各项的公因式。
am+bm
=m(a+b)
1.探索新知
左边的这个多项式有什么特点呢？
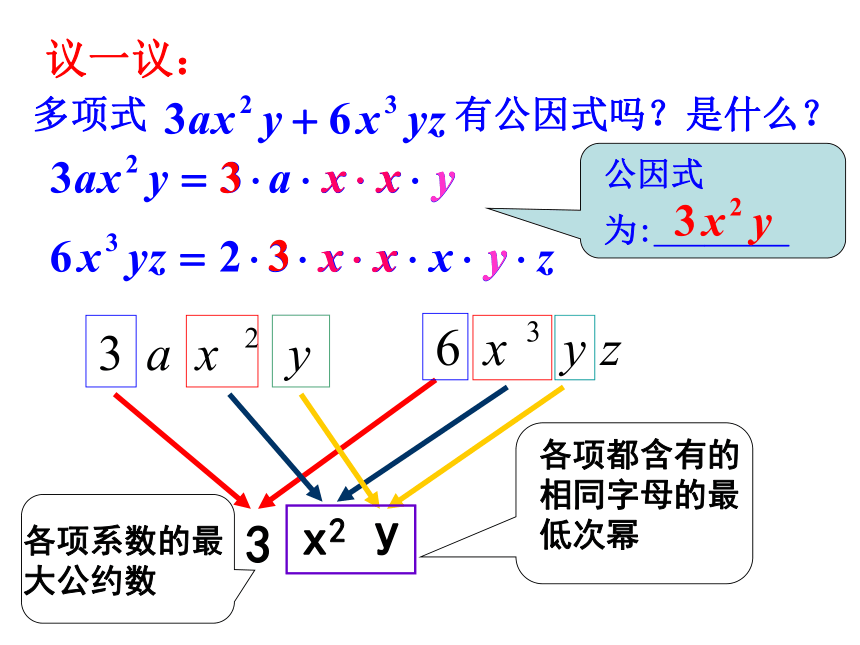
议一议：
多项式　　　　　　　　有公因式吗？是什么？
公因式为:________
3
x2
y
各项系数的最
大公约数
各项都含有的
相同字母的最
低次幂
2.字母:提取相同字母最低次幂。
1.系数:提取最大的公约数;
判断公因式的方法:
3
a
5b2
（b-c）
3a2b
说一说下列各式的公因式
多项式的公因式都有哪些形式啊？
分解因式：
解：
用公因式去除多项式,所得的商为另一个因式
公因式是:
(1)问： , 是如何得到的？
注意:提取公因式后, 余下的多项式不再含有公因式
2.提取公因式法:
如果一个多项式的各项含有公因式，那么就可以把这个公因式提出来，从而将多项式化成两个因式乘积的形式，这种分解因式的方法叫做提取公因式法。
练一练：
多项式 公因式
因式分解结果
① 确定应提取的公因式
②用公因式去除多项式,所得的商为另一个因式
③ 把多项式写成这两个因式积的形式
提取公因式法的一般步骤:
例1：确定下列多项式的
公因式，并分解因式
2.例题解析
当首项的系数为负时,通常应先提取负号,此 时需添加括号，且括号内的各项都改变符号.
（3） (2a-b)2 +2a – b = (2a –b)2 + ( )
（4）a ( s + t ) –s – t = a ( s + t ) – ( )
回顾去括号法则，完成下列填空：
（1）1-x =+( );（2）-x+1= – ( )
你能概括出添括号法则吗？
1 -x
x-1
括号前面是“+”号，括到括号里的各项都不变号；
括号前面是“-”号，括到括号里的各项都变号。
热身训练
2a - b
s + t
提取公因式时，有时需要将因式经过符号变换、字母位置重新排列或添括号后，才能看出公因式。
解:
例2、把 分解因式
将 变换成
[添加括号]
[提取公因式(a －b)]
错
错
错
错
1.下面的分解因式对吗？如果不对，应怎样改正？
3.巩固与提高
a(x-y)+bx-by
变式1：a(x-y)+by-bx
变式2： a(x-y)3+b(y-x)2
确定公因式
①系数:提取最大的公约数;
②字母:提取相同字母最低次幂。
4.课堂小结
2、提取公因式法分解因式步骤
3、添括号法则
① 确定应提取的公因式
②用公因式去除多项式,所得的商为另一个因式
③ 把多项式写成这两个因式积的形式
括号前面是“+”号，括到括号里的各项都不变号；
括号前面是“—”号，括到括号里的是各项都变号.
提取公因式法口决
公因式看过来，系数字母都包含；
公因式提出来，其余项数不要改；
公因式躲起来，整体换元帮忙看；
公因式并不难，认真学习定过关。
6.口诀