1.4平行线的性质(1)课件(共20张PPT)
文档属性
| 名称 | 1.4平行线的性质(1)课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-24 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
浙教版
七年级下
1.4
平行线的性质(1)
探索与发现
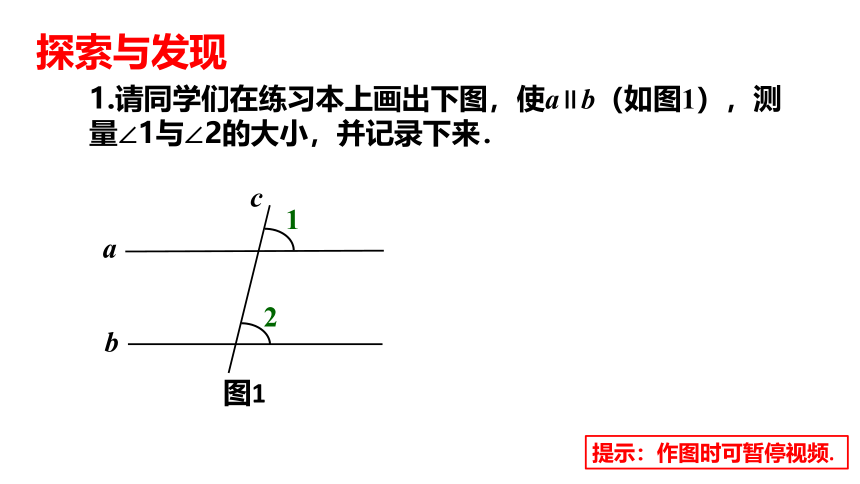
1.请同学们在练习本上画出下图,使a∥b(如图1),测量∠1与∠2的大小,并记录下来.
提示:作图时可暂停视频.
c
a
b
1
2
图1
探索与发现
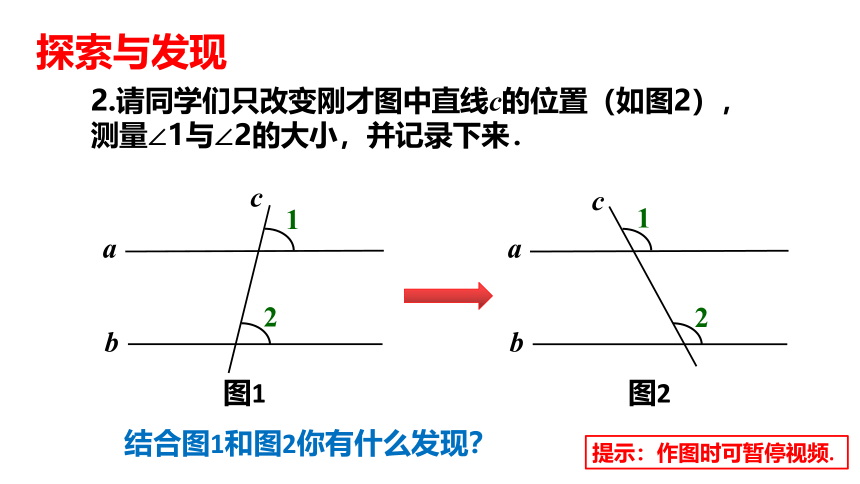
2.请同学们只改变刚才图中直线c的位置(如图2),测量∠1与∠2的大小,并记录下来.
a
b
c
1
2
图2
c
a
b
1
2
图1
结合图1和图2你有什么发现?
提示:作图时可暂停视频.
探索与发现
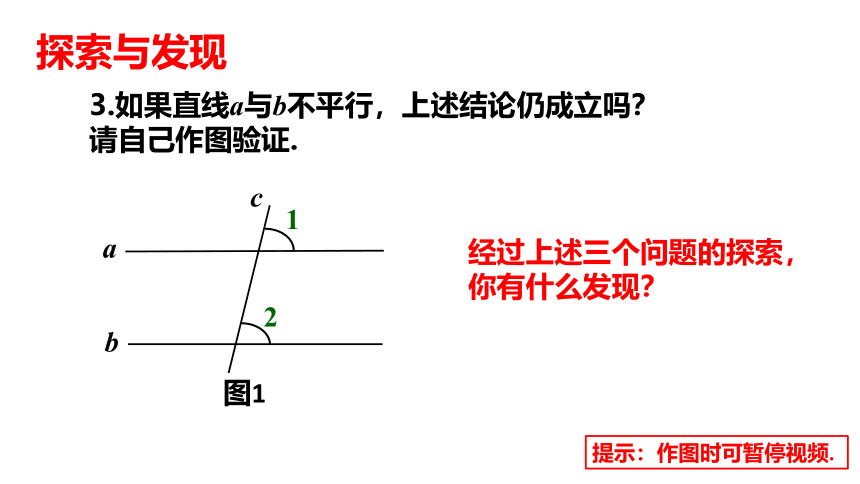
3.如果直线a与b不平行,上述结论仍成立吗?请自己作图验证.
经过上述三个问题的探索,你有什么发现?
c
a
b
1
2
图1
提示:作图时可暂停视频.
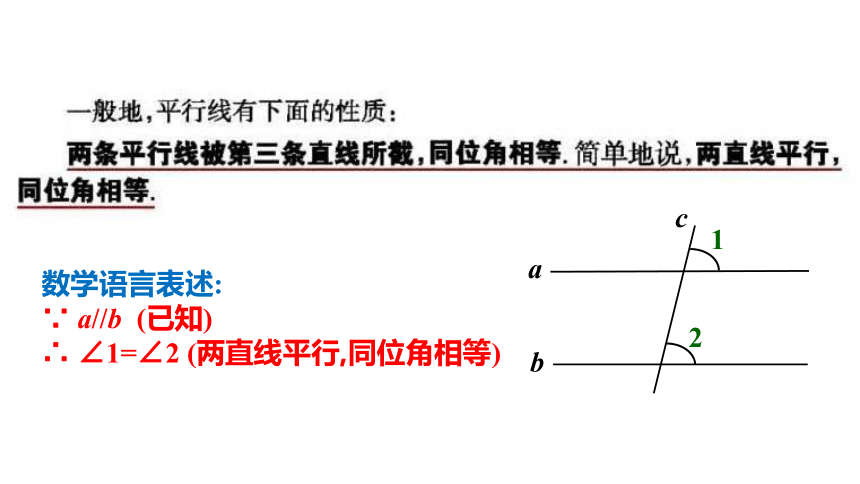
数学语言表述:
∵
a//b
(已知)
∴
∠1=∠2
(两直线平行,同位角相等)
c
a
b
1
2
问题与思考
平行线的判定:同位角相等,两直线平行.
平行线的性质:两直线平行,同位角相等.
1.平行线的判定与性质的条件与结论有什么关系?
2.使用判定时是已知
,说明
;
角相等
两直线平行
3.使用性质时是已知
,说明
.
两直线平行
角相等
互换
分析与归纳
例1、如图,梯子的各条横档互相平行,∠1=100°,求∠2的度数.
A
B
C
D
1
2
3
1.由梯子的各条横档互相平行可以得出什么结论?
2.∠1,∠2的位置是不是我们熟悉位置的角?
3.还需要什么样的角才能把∠1,∠2都联系起来?
4.这样的角你能找到几个?
思考
如:构造∠3
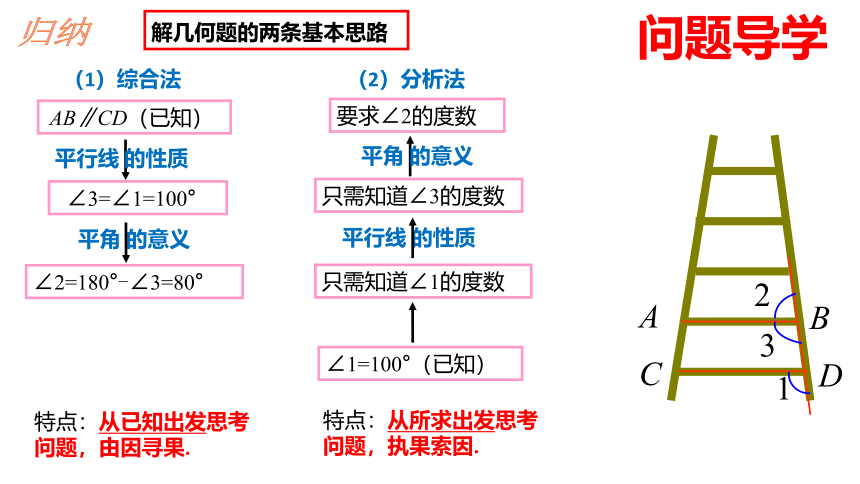
AB∥CD(已知)
∠3=∠1=100°
只需知道∠3的度数
∠2=180°-∠3=80°
问题导学
要求∠2的度数
只需知道∠1的度数
∠1=100°(已知)
(1)综合法
(2)分析法
平行线
的性质
平角
的意义
A
B
C
D
1
2
3
平行线
的性质
平角
的意义
特点:从已知出发思考问题,由因寻果.
特点:从所求出发思考问题,执果索因.
解几何题的两条基本思路
归纳
例1、如图,梯子的各条横档互相平行,∠1=100°,求∠2的度数.
解析
书本样例
你还有其他证明方法吗?
对应练习:
对比阅读,两种书写格式均可
∠2=40°
解:∵AB∥CD(已知)
∴∠3=∠1=100°
(两直线平行,同位角相等)
∵∠2+∠3=180°
(平角的意义)
∴∠2=180°-∠3==80°
分析与归纳
例2、如图,已知∠1=∠2.若直线b⊥m,则直线a⊥m.请说明理由.
1.先从所求出发考虑问题,要说明a⊥m,只需要说明什么?
2.根据已知b⊥m,能得出什么结论?
3.问题归结为只要说明那两条直线平行?
4.根据已知∠1=∠2,又能推出什么?
思考
a
b
m
n
1
2
3
4
分析
a
b
m
n
1
2
3
4
只需知道∠3=90°
要证a⊥m
只需要a∥b
∠1=∠2(已知)
平行线
的判定
垂直
的意义
而b⊥m,可得∠4=90°
只需要证∠3=∠4
平行线
的性质
问题导学
例2、如图,已知∠1=∠2.若直线b⊥m,则直线a⊥m.请说明理由.
解析
对应练习:
书本样例
对比阅读,两种书写格式均可
你会吗?
证明:∵∠1=∠2(已知)
∴a∥b(同位角相等,两直线平行)
∴∠3=∠4(两直线平行,同位角相等)
∵b⊥m
∴∠4=90°(垂直的意义)
∴∠3=90°
∴a⊥m
内错角相等,两直线平行
两直线平行,同位角相等
l1
l2
第一个算出地球周长的人
2000多年前,有人用简单的测量工具计算出地球的周长。这个人就是古希腊的爱拉斯托塞.
细心的爱拉斯托塞发现:离亚历山大城A约785公里的塞尼城S,夏日正午的阳光可以一直照到井底,也就是说,在那一时刻,太阳正好悬挂在塞尼城的正上方E,阳光能够只指地心O.而在此时他所在的亚历山大城阳光却不能直接射到水井的底部.爱拉斯托塞在地上竖起一根小木棍AC,测量天顶方向AB与太阳方向AD之间的夹角∠1,发现这个夹角等于360°的1/50
.
E
D
B
1
S
A
O
2
C
由于太阳离地球非常遥远,把射到地球上的阳光看作是彼此平行的,即AD
∥SE,根据:两直线平行,同位角相等.所以∠1=
∠2.
那么∠2的度数也等于360°的1/50
,所以,亚历山大城到塞尼城的距离弧AS也等于整个地球周长的1/50
.而亚历山大城到塞尼城的距离约为785公里,785×50=369250公里,这是一个相当精确的结果.
地球周长测出来啦!
E
D
B
1
S
A
O
2
C
课堂小结
c
a
b
1
2
平行线的性质:两直线平行,
同位角相等.
平行线的判定:
同位角相等,
两直线平行.
区别
联系
解几何题的两条基本思路:
综合法、分析法
两直线平行,
内错角有什么关系?同旁内角呢?
学习检测:
1.如图,∠B=60°,AB//CD,则∠CDE=
.
A
B
C
D
E
3.如图,折叠一张矩形纸片,已知∠1=70°,则∠2=
.
2.如图,在Rt△ABC中,D为边CA延长线上一点,DE//AB,∠ADE=42°,则∠B=____.
第1题图
第3题图
第2题图
学习检测:
c
a
b
1
2
3
4.如图,已知a∥b,∠1=75°,分别求∠2,∠3的度数.
第4题图
5.如图,已知AB//CD,DE//BC.
(1)判断∠B和∠D的数量关系,并说明理由.
(2)设∠B=(x+15)°,∠D=(75-3x)°求∠1的度数.
A
E
D
C
B
1
第5题图
学习检测答案:
1.
60°
2.
48°
3.
55°
4.解:∵a∥b(已知)
∴∠2=∠1=75°(两直线平行,同位角相等)
∵∠2+∠3=180°(平角的意义)
∴∠3=180°-∠2=180°-75°=105°
5.解:(1)∠B=∠D
理由如下:∵AB//CD,DE//BC(已知)
∴∠B=∠1,∠D=∠1(两直线平行,同位角相等)
∴∠B=∠D
(2)由(1)中得∠B=∠D,则
x+15=75-3x,解得
x=15,
∴∠B=(x+15)°=30°
∵AB//CD
∴∠1=∠B=30°
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
浙教版
七年级下
1.4
平行线的性质(1)
探索与发现
1.请同学们在练习本上画出下图,使a∥b(如图1),测量∠1与∠2的大小,并记录下来.
提示:作图时可暂停视频.
c
a
b
1
2
图1
探索与发现
2.请同学们只改变刚才图中直线c的位置(如图2),测量∠1与∠2的大小,并记录下来.
a
b
c
1
2
图2
c
a
b
1
2
图1
结合图1和图2你有什么发现?
提示:作图时可暂停视频.
探索与发现
3.如果直线a与b不平行,上述结论仍成立吗?请自己作图验证.
经过上述三个问题的探索,你有什么发现?
c
a
b
1
2
图1
提示:作图时可暂停视频.
数学语言表述:
∵
a//b
(已知)
∴
∠1=∠2
(两直线平行,同位角相等)
c
a
b
1
2
问题与思考
平行线的判定:同位角相等,两直线平行.
平行线的性质:两直线平行,同位角相等.
1.平行线的判定与性质的条件与结论有什么关系?
2.使用判定时是已知
,说明
;
角相等
两直线平行
3.使用性质时是已知
,说明
.
两直线平行
角相等
互换
分析与归纳
例1、如图,梯子的各条横档互相平行,∠1=100°,求∠2的度数.
A
B
C
D
1
2
3
1.由梯子的各条横档互相平行可以得出什么结论?
2.∠1,∠2的位置是不是我们熟悉位置的角?
3.还需要什么样的角才能把∠1,∠2都联系起来?
4.这样的角你能找到几个?
思考
如:构造∠3
AB∥CD(已知)
∠3=∠1=100°
只需知道∠3的度数
∠2=180°-∠3=80°
问题导学
要求∠2的度数
只需知道∠1的度数
∠1=100°(已知)
(1)综合法
(2)分析法
平行线
的性质
平角
的意义
A
B
C
D
1
2
3
平行线
的性质
平角
的意义
特点:从已知出发思考问题,由因寻果.
特点:从所求出发思考问题,执果索因.
解几何题的两条基本思路
归纳
例1、如图,梯子的各条横档互相平行,∠1=100°,求∠2的度数.
解析
书本样例
你还有其他证明方法吗?
对应练习:
对比阅读,两种书写格式均可
∠2=40°
解:∵AB∥CD(已知)
∴∠3=∠1=100°
(两直线平行,同位角相等)
∵∠2+∠3=180°
(平角的意义)
∴∠2=180°-∠3==80°
分析与归纳
例2、如图,已知∠1=∠2.若直线b⊥m,则直线a⊥m.请说明理由.
1.先从所求出发考虑问题,要说明a⊥m,只需要说明什么?
2.根据已知b⊥m,能得出什么结论?
3.问题归结为只要说明那两条直线平行?
4.根据已知∠1=∠2,又能推出什么?
思考
a
b
m
n
1
2
3
4
分析
a
b
m
n
1
2
3
4
只需知道∠3=90°
要证a⊥m
只需要a∥b
∠1=∠2(已知)
平行线
的判定
垂直
的意义
而b⊥m,可得∠4=90°
只需要证∠3=∠4
平行线
的性质
问题导学
例2、如图,已知∠1=∠2.若直线b⊥m,则直线a⊥m.请说明理由.
解析
对应练习:
书本样例
对比阅读,两种书写格式均可
你会吗?
证明:∵∠1=∠2(已知)
∴a∥b(同位角相等,两直线平行)
∴∠3=∠4(两直线平行,同位角相等)
∵b⊥m
∴∠4=90°(垂直的意义)
∴∠3=90°
∴a⊥m
内错角相等,两直线平行
两直线平行,同位角相等
l1
l2
第一个算出地球周长的人
2000多年前,有人用简单的测量工具计算出地球的周长。这个人就是古希腊的爱拉斯托塞.
细心的爱拉斯托塞发现:离亚历山大城A约785公里的塞尼城S,夏日正午的阳光可以一直照到井底,也就是说,在那一时刻,太阳正好悬挂在塞尼城的正上方E,阳光能够只指地心O.而在此时他所在的亚历山大城阳光却不能直接射到水井的底部.爱拉斯托塞在地上竖起一根小木棍AC,测量天顶方向AB与太阳方向AD之间的夹角∠1,发现这个夹角等于360°的1/50
.
E
D
B
1
S
A
O
2
C
由于太阳离地球非常遥远,把射到地球上的阳光看作是彼此平行的,即AD
∥SE,根据:两直线平行,同位角相等.所以∠1=
∠2.
那么∠2的度数也等于360°的1/50
,所以,亚历山大城到塞尼城的距离弧AS也等于整个地球周长的1/50
.而亚历山大城到塞尼城的距离约为785公里,785×50=369250公里,这是一个相当精确的结果.
地球周长测出来啦!
E
D
B
1
S
A
O
2
C
课堂小结
c
a
b
1
2
平行线的性质:两直线平行,
同位角相等.
平行线的判定:
同位角相等,
两直线平行.
区别
联系
解几何题的两条基本思路:
综合法、分析法
两直线平行,
内错角有什么关系?同旁内角呢?
学习检测:
1.如图,∠B=60°,AB//CD,则∠CDE=
.
A
B
C
D
E
3.如图,折叠一张矩形纸片,已知∠1=70°,则∠2=
.
2.如图,在Rt△ABC中,D为边CA延长线上一点,DE//AB,∠ADE=42°,则∠B=____.
第1题图
第3题图
第2题图
学习检测:
c
a
b
1
2
3
4.如图,已知a∥b,∠1=75°,分别求∠2,∠3的度数.
第4题图
5.如图,已知AB//CD,DE//BC.
(1)判断∠B和∠D的数量关系,并说明理由.
(2)设∠B=(x+15)°,∠D=(75-3x)°求∠1的度数.
A
E
D
C
B
1
第5题图
学习检测答案:
1.
60°
2.
48°
3.
55°
4.解:∵a∥b(已知)
∴∠2=∠1=75°(两直线平行,同位角相等)
∵∠2+∠3=180°(平角的意义)
∴∠3=180°-∠2=180°-75°=105°
5.解:(1)∠B=∠D
理由如下:∵AB//CD,DE//BC(已知)
∴∠B=∠1,∠D=∠1(两直线平行,同位角相等)
∴∠B=∠D
(2)由(1)中得∠B=∠D,则
x+15=75-3x,解得
x=15,
∴∠B=(x+15)°=30°
∵AB//CD
∴∠1=∠B=30°
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
