1.4平行线的性质(2)课件(共21张PPT)
文档属性
| 名称 | 1.4平行线的性质(2)课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-24 14:04:21 | ||
图片预览







文档简介
(共21张PPT)
浙教版
七年级下
1.4
平行线的性质(2)
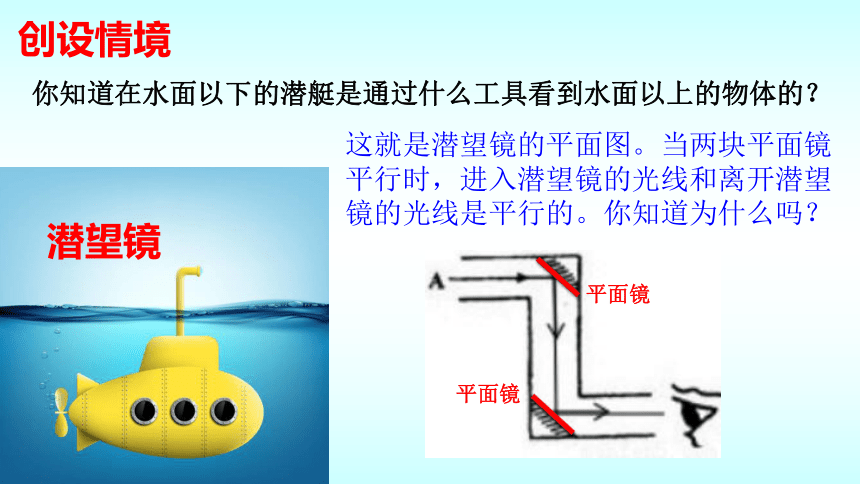
这就是潜望镜的平面图。当两块平面镜平行时,进入潜望镜的光线和离开潜望镜的光线是平行的。你知道为什么吗?
潜望镜
你知道在水面以下的潜艇是通过什么工具看到水面以上的物体的?
平面镜
平面镜
创设情境
探索与发现
(1)∵
AB∥CD
(已知)
∴
∠1=∠2
(两直线平行,同位角相等)
∵
∠1=∠3
(对顶角相等)
∴
∠2=∠3
(等量代换)
(2)
∵
∠2=∠3
(已证)
又∵
∠2+
∠4=180
°
(平角的意义)
∴
∠3+
∠4=180
°
(等量代换)
∠1=∠2
∠3=∠1
∠4与∠2互补
两直线平行,同位角相等
温馨提醒:本节课中,如果有需要都可以暂停视频.
∠2和∠3是一对什么角?
∠3和∠4是一对什么角?
内错角
同旁内角
转化思想
探索与发现
数学语言表述:
∵
AB//CD
(已知)
∴
∠2=∠3
(两直线平行,内错角相等)
数学语言表述:
∵
AB//CD
(已知)
∴
∠3+∠4=180°
(两直线平行,同旁内角互补)
你能试着写出上述两条平行线性质的数学语言吗?
平行线的性质
(1)两直线平行,同位角相等.
数学语言表述:
∵
AB//CD
(已知)
∴
∠1=∠2
(两直线平行,同位角相等)
(2)两直线平行,内错角相等.
数学语言表述:
∵
AB//CD
(已知)
∴
∠2=∠3
(两直线平行,内错角相等)
(3)两直线平行,同旁内角互补.
数学语言表述:
∵
AB//CD
(已知)
∴
∠3+∠4=180°
(两直线平行,同旁内角互补)
条件?结论?
两条平行线得到角的数量关系
性质巩固
两直线平行,内错角相等
两直线平行,同旁内角互补
120°
180°
60°
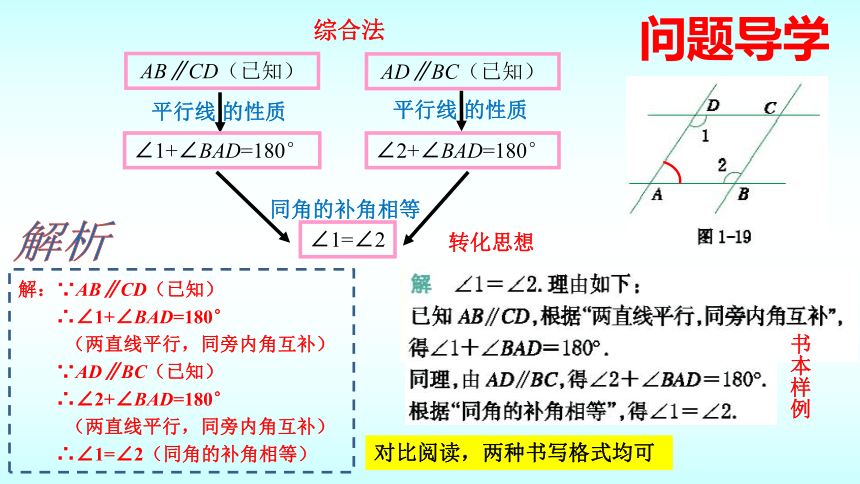
问题与思考一
思考
1.从已知出发思考问题,由已知AB∥CD,能推出∠1与哪个角有怎么样的关系?
2.同理,由已知AD∥BC,能推出∠2与哪个角有怎么样的关系?
3.根据1,2,可以说明∠1与∠2相等吗?为什么?
4.你还有哪些方法可以证明本题?
如:构造∠BAD
温馨提醒:思考时可暂停视频.
平行线
的性质
平行线
的性质
AB∥CD(已知)
∠1+∠BAD=180°
∠1=∠2
综合法
同角的补角相等
问题导学
AD∥BC(已知)
∠2+∠BAD=180°
解:∵AB∥CD(已知)
∴∠1+∠BAD=180°
(两直线平行,同旁内角互补)
∵AD∥BC(已知)
∴∠2+∠BAD=180°
(两直线平行,同旁内角互补)
∴∠1=∠2(同角的补角相等)
书本样例
解析
对比阅读,两种书写格式均可
转化思想
内错角+内错角(Z+Z)
你还有其他想法吗?
思维发散
同旁内角+同旁内角(U+U)
同位角+内错角(F+Z)
3
4
5
6
添辅助线,分割角
解:∵AB∥CD
∴∠3=∠6
(两直线平行,内错角相等)
∵
AD∥BC
∴∠4=∠5
(两直线平行,内错角相等)
∴
∠3+
∠4=∠5+∠6
∴
∠ADC=∠ABC
小结:①在无法直接证明两个量的关系时,可以通过找一个中间量把两个量联系起来.(转化)
②在复杂图形中,可以通过寻找基本图形来帮助我们解决问题.
角的数量关系
线的位置关系
两直线平行
同旁内角互补
内错角相等
同位角相等
性质
判定
归纳
问题与思考二
思考
1.由已知BD平分∠ABC可以推出什么?
2.由所求,需要说明哪两个角相等?能转换成∠ABD=∠D吗?
3.要说明∠ABD=∠D,需要说明什么?
4.根据什么条件可以说明AB∥CD,依据是什么?
温馨提醒:思考时可暂停视频.
平行线
的判定
平行线
的性质
∠ABC+∠C=180°
AB∥CD
∠ABD=∠D
问题导学
BD平分∠ABC
∠ABD=∠CBD
∠CBD=∠D
等量代换
解析
解:∠CBD=∠D.
理由如下:∵∠ABC+∠C=180°
∴AB∥CD(同旁内角互补,两直线平行)
∴∠ABD=∠D(两直线平行,内错角相等)
∵BD平分∠ABC
∴∠ABD=∠CBD
∴∠CBD=∠D
书本样例
转化思想
变式练习
如图,已知BD平分∠ABC,∠CBD=∠D.
求证:∠ABC+∠C=180°
证明:∵BD平分∠ABC
∴∠ABD=∠CBD
∵∠CBD=∠D
∴∠ABD=∠D
∴AB∥CD
(内错角相等,两直线平行)
∴∠ABC+∠C=180°(两直线平行,同旁内角互补)
条件和结论互换
潜望镜中的两个镜子MN、EF是平行放置的,光线经过镜子反射时,∠1=∠2,∠3=∠4,请说明为什么进入潜望镜的光线AB和离开潜望镜的光线CD是平行的?
学以致用
F
1
2
3
A
B
C
D
M
N
E
4
思考
1.由已知MN、EF是平行放置的,可以得出什么结论?
2.由已知∠1=∠2,∠3=∠4可以得出什么?
3.根据什么条件可以说明AB∥CD,依据是什么?
温馨提醒:思考时可暂停视频.
5
6
F
1
2
3
A
B
C
D
M
N
E
4
证明
:∵MN∥EF
∴∠2=∠3
(两直线平行,内错角相等)
∵∠1=∠2
,∠3=∠4
∴∠1=∠2
=∠3=∠4(等量代换)
∵∠1+∠2
+∠5=180?,
∠3+∠4
+∠6=180?
∴∠5=∠6
∴AB∥CD(内错角相等,两直线平行)
解析
潜望镜的原理我们明白了!
课堂小结
平行线的性质:两直线平行,
同位角相等、
内错角相等、
同旁内角互补.
平行线的判定:
同位角相等、
内错角相等、
同旁内角互补,
两直线平行.
区别
联系
思想方法:
转化思想
利用平行线的性质和判定解决问题:寻找基本图形
第3题图
学习检测:
1.如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠2=80°,则∠1等于( )
A.120°
B.110°
C.100°
D.80°
3.如图,直线m∥n,∠1=70°,∠2=28°,则∠A=
.
2.如图,直线l1∥l2,CD⊥AB于点D,∠1=50°,则∠BCD=
.
第1题图
第2题图
学习检测:
4.如图,直线AB,CD分别与直线AC相交于点A,C,与直线BD相交于点B,D.若∠1=∠2,∠3=75°,求∠4的度数.
第4题图
5.如图,CD∥EF,∠1=∠2,求证:∠3=∠ACB.
第5题图
学习检测答案:
1.
C
2.
40°
3.
42°
4.
解:∵∠1=∠2(已知)
∴AB//CD(同位角相等,两直线平行)
∴∠4=∠3=75°(两直线平行,内错角相等)
5.
解:∵CD∥EF(已知)
∴∠DCB=∠2(两直线平行,同位角相等)
∵∠1=∠2
∴∠DCB=∠1
∴BC
//
DG(内错角角相等,两直线平行)
∴∠3=∠ACB(两直线平行,同位角相等)
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
浙教版
七年级下
1.4
平行线的性质(2)
这就是潜望镜的平面图。当两块平面镜平行时,进入潜望镜的光线和离开潜望镜的光线是平行的。你知道为什么吗?
潜望镜
你知道在水面以下的潜艇是通过什么工具看到水面以上的物体的?
平面镜
平面镜
创设情境
探索与发现
(1)∵
AB∥CD
(已知)
∴
∠1=∠2
(两直线平行,同位角相等)
∵
∠1=∠3
(对顶角相等)
∴
∠2=∠3
(等量代换)
(2)
∵
∠2=∠3
(已证)
又∵
∠2+
∠4=180
°
(平角的意义)
∴
∠3+
∠4=180
°
(等量代换)
∠1=∠2
∠3=∠1
∠4与∠2互补
两直线平行,同位角相等
温馨提醒:本节课中,如果有需要都可以暂停视频.
∠2和∠3是一对什么角?
∠3和∠4是一对什么角?
内错角
同旁内角
转化思想
探索与发现
数学语言表述:
∵
AB//CD
(已知)
∴
∠2=∠3
(两直线平行,内错角相等)
数学语言表述:
∵
AB//CD
(已知)
∴
∠3+∠4=180°
(两直线平行,同旁内角互补)
你能试着写出上述两条平行线性质的数学语言吗?
平行线的性质
(1)两直线平行,同位角相等.
数学语言表述:
∵
AB//CD
(已知)
∴
∠1=∠2
(两直线平行,同位角相等)
(2)两直线平行,内错角相等.
数学语言表述:
∵
AB//CD
(已知)
∴
∠2=∠3
(两直线平行,内错角相等)
(3)两直线平行,同旁内角互补.
数学语言表述:
∵
AB//CD
(已知)
∴
∠3+∠4=180°
(两直线平行,同旁内角互补)
条件?结论?
两条平行线得到角的数量关系
性质巩固
两直线平行,内错角相等
两直线平行,同旁内角互补
120°
180°
60°
问题与思考一
思考
1.从已知出发思考问题,由已知AB∥CD,能推出∠1与哪个角有怎么样的关系?
2.同理,由已知AD∥BC,能推出∠2与哪个角有怎么样的关系?
3.根据1,2,可以说明∠1与∠2相等吗?为什么?
4.你还有哪些方法可以证明本题?
如:构造∠BAD
温馨提醒:思考时可暂停视频.
平行线
的性质
平行线
的性质
AB∥CD(已知)
∠1+∠BAD=180°
∠1=∠2
综合法
同角的补角相等
问题导学
AD∥BC(已知)
∠2+∠BAD=180°
解:∵AB∥CD(已知)
∴∠1+∠BAD=180°
(两直线平行,同旁内角互补)
∵AD∥BC(已知)
∴∠2+∠BAD=180°
(两直线平行,同旁内角互补)
∴∠1=∠2(同角的补角相等)
书本样例
解析
对比阅读,两种书写格式均可
转化思想
内错角+内错角(Z+Z)
你还有其他想法吗?
思维发散
同旁内角+同旁内角(U+U)
同位角+内错角(F+Z)
3
4
5
6
添辅助线,分割角
解:∵AB∥CD
∴∠3=∠6
(两直线平行,内错角相等)
∵
AD∥BC
∴∠4=∠5
(两直线平行,内错角相等)
∴
∠3+
∠4=∠5+∠6
∴
∠ADC=∠ABC
小结:①在无法直接证明两个量的关系时,可以通过找一个中间量把两个量联系起来.(转化)
②在复杂图形中,可以通过寻找基本图形来帮助我们解决问题.
角的数量关系
线的位置关系
两直线平行
同旁内角互补
内错角相等
同位角相等
性质
判定
归纳
问题与思考二
思考
1.由已知BD平分∠ABC可以推出什么?
2.由所求,需要说明哪两个角相等?能转换成∠ABD=∠D吗?
3.要说明∠ABD=∠D,需要说明什么?
4.根据什么条件可以说明AB∥CD,依据是什么?
温馨提醒:思考时可暂停视频.
平行线
的判定
平行线
的性质
∠ABC+∠C=180°
AB∥CD
∠ABD=∠D
问题导学
BD平分∠ABC
∠ABD=∠CBD
∠CBD=∠D
等量代换
解析
解:∠CBD=∠D.
理由如下:∵∠ABC+∠C=180°
∴AB∥CD(同旁内角互补,两直线平行)
∴∠ABD=∠D(两直线平行,内错角相等)
∵BD平分∠ABC
∴∠ABD=∠CBD
∴∠CBD=∠D
书本样例
转化思想
变式练习
如图,已知BD平分∠ABC,∠CBD=∠D.
求证:∠ABC+∠C=180°
证明:∵BD平分∠ABC
∴∠ABD=∠CBD
∵∠CBD=∠D
∴∠ABD=∠D
∴AB∥CD
(内错角相等,两直线平行)
∴∠ABC+∠C=180°(两直线平行,同旁内角互补)
条件和结论互换
潜望镜中的两个镜子MN、EF是平行放置的,光线经过镜子反射时,∠1=∠2,∠3=∠4,请说明为什么进入潜望镜的光线AB和离开潜望镜的光线CD是平行的?
学以致用
F
1
2
3
A
B
C
D
M
N
E
4
思考
1.由已知MN、EF是平行放置的,可以得出什么结论?
2.由已知∠1=∠2,∠3=∠4可以得出什么?
3.根据什么条件可以说明AB∥CD,依据是什么?
温馨提醒:思考时可暂停视频.
5
6
F
1
2
3
A
B
C
D
M
N
E
4
证明
:∵MN∥EF
∴∠2=∠3
(两直线平行,内错角相等)
∵∠1=∠2
,∠3=∠4
∴∠1=∠2
=∠3=∠4(等量代换)
∵∠1+∠2
+∠5=180?,
∠3+∠4
+∠6=180?
∴∠5=∠6
∴AB∥CD(内错角相等,两直线平行)
解析
潜望镜的原理我们明白了!
课堂小结
平行线的性质:两直线平行,
同位角相等、
内错角相等、
同旁内角互补.
平行线的判定:
同位角相等、
内错角相等、
同旁内角互补,
两直线平行.
区别
联系
思想方法:
转化思想
利用平行线的性质和判定解决问题:寻找基本图形
第3题图
学习检测:
1.如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠2=80°,则∠1等于( )
A.120°
B.110°
C.100°
D.80°
3.如图,直线m∥n,∠1=70°,∠2=28°,则∠A=
.
2.如图,直线l1∥l2,CD⊥AB于点D,∠1=50°,则∠BCD=
.
第1题图
第2题图
学习检测:
4.如图,直线AB,CD分别与直线AC相交于点A,C,与直线BD相交于点B,D.若∠1=∠2,∠3=75°,求∠4的度数.
第4题图
5.如图,CD∥EF,∠1=∠2,求证:∠3=∠ACB.
第5题图
学习检测答案:
1.
C
2.
40°
3.
42°
4.
解:∵∠1=∠2(已知)
∴AB//CD(同位角相等,两直线平行)
∴∠4=∠3=75°(两直线平行,内错角相等)
5.
解:∵CD∥EF(已知)
∴∠DCB=∠2(两直线平行,同位角相等)
∵∠1=∠2
∴∠DCB=∠1
∴BC
//
DG(内错角角相等,两直线平行)
∴∠3=∠ACB(两直线平行,同位角相等)
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
