6.3用乘法公式分解因式

(共19张PPT)
下列等式中，哪些是因式分解？哪些不是？为什么？
一个多项式
几个整式的积
有一个必定是多项式
最后一步运算是乘法
练一练：分解因式
公因式：
各项系数的最大公因式
各项都含有的相同字母的最低次幂
×
提取公因式法的一般步骤：
（1）确定应提取的公因式
（2）多项式除以公因式，所得的商作为另一个因式
（3）把多项式写成这两个因式的积的形式
6.3 用乘法公式分解公式(1)
把一张如图形状的卡纸剪开，拼成一张长方形卡纸，作为一幅精美剪纸的衬底，你认为该怎么剪？
a
b
a
a-b
b
a-b
a+b
两种形状的纸的面积之间有什么关系？它验证了一个什么公式？
两个数的平方差=这两个数的和与这两个数的差的积。
两个数的和与这两个数的差的积=这两个数的平方差。
都叫作平方差公式
整式乘法：
因式分解：
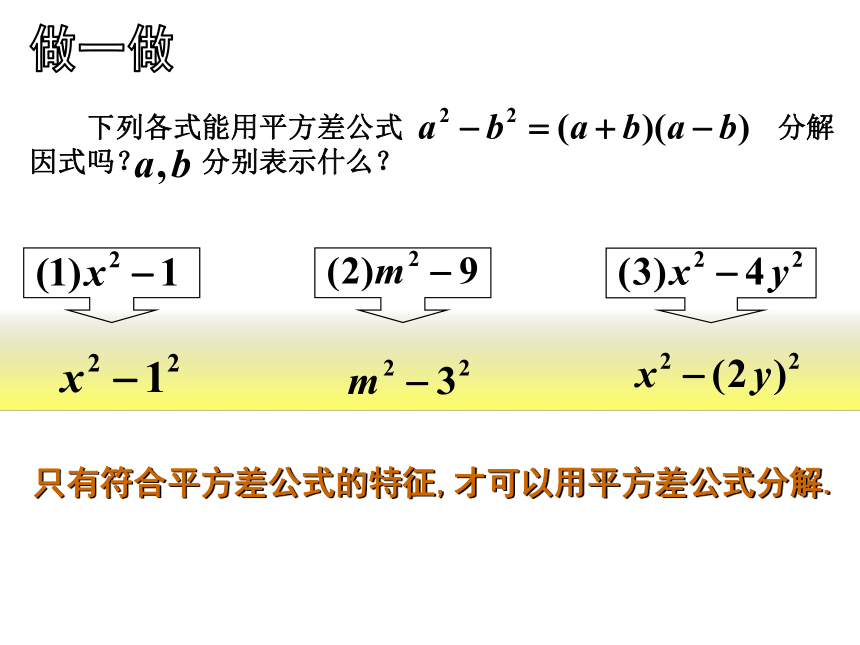
　　下列各式能用平方差公式　　　　　　　　　　　　　分解因式吗？　　分别表示什么？
只有符合平方差公式的特征,才可以用平方差公式分解.
（１）公式左边：
（是一个将要被分解因式的多项式）
★被分解的多项式含有两项，且这两项异号，并且能写成（　）２－（　）２的形式。
)
)(
(
2
2
b
a
b
a
b
a
-
+
=
-
▲
▲
▲
说一说：
下列多项式能转化成（　）２－（　）２的形式吗？如果能，请将其转化成（　）２－（　）２的形式。
(1) m2 －1
(2)4m2 －9
(3)4m2+9
(4)x2 －25y 2
(5) －x2 －25y2
(6) －x2+25y2
= m2 －12
= (2m)2 －32
不能转化为平方差形式
＝ x2 －(5y)2
不能转化为平方差形式
= 25y2－x2 =(5y)2 －x2
a2 － b2= (a ＋ b) (a － b)
（１）公式左边：
（是一个将要被分解因式的多项式）
★被分解的多项式含有两项，且这两项异号，并且能写成（　）２－（　）２的形式。
)
)(
(
2
2
b
a
b
a
b
a
-
+
=
-
▲
▲
▲
说一说：
(2) 公式右边:
（是分解因式的结果）
★分解的结果是两个底数的和乘以两个底数的差的形式。
把上题中写成平方差形式的多项式，进行因式分解。
(1) m2 －1
(2)4m2 －9
(3)4m2+9
(4)x2 －25y 2
(5) －x2 －25y2
(6) －x2+25y2
= m2 －12
= (2m)2 －32
不能转化为平方差形式
＝ x2 －(5y)2
不能转化为平方差形式
= 25y2－x2 = (5y)2 －x2
=（m+1）(m－1)
=（2m+3）(2m －3)
= (x+5y)(x －5y)
= (5y+x)(5y － x)
a2 － b2= (a ＋ b) (a － b)
例1：把下列各式分解因式：
参照对象：
)
)(
(
2
2
b
a
b
a
b
a
-
+
=
-
20062－20052 =
（2mn）2 - ( 3xy)2 =
(n+2)2 - (n-3)2 =
结论：
公式中的a、b无论表示数、单项式、还是多项式，只要被分解的多项式能转化成平方差的形式，就能用平方差公式因式分解。
例2：分解因式：
（2）因式分解要彻底，直到不能分解为止。
（1）因式分解时，通常先考虑提取公因式法，然后再考虑其他法。
先提取公因式，后用平方差公式
分解因式：
先提取公因式，后用平方差公式
两次运用平方差公式
（1）用简便方法计算：
（2）把9991分解成两个整数的积。
(1) x2-1 (2)m2-9
(3)x2-4y2 (4) 25x2-4
(5) 0.01s2-t2 (6) 121-4a2b2
(7) a6-81 (8) –x2+25
(9) 16a2-9b2 (10) - 4a2b2+c2
=(x+1)(x-1)
=(m+3)(m-3)
=(x+2y)(x-2y)
=(5x+2)(5x-2)
=(0.1s+t)(0.1s-t)
=(11+2ab)(11-2ab)
=(a3+9)(a3-9)
=(5+x)(5-x)
=(4a+3b)(4a-3b)
=(c+2ab)(c-2ab)