7.4 分式方程(1)

(共27张PPT)
《数学》(浙江版 七年级 下册)
7.4 分式方程(1)
分式方程的概念及解法
某地电话公司调低了长途电话的话费标准，每分费用降低了25％，因此按原收费标准6元话费的通话时间，在新收费标准下可多通话5分时间，问前后两种收费标准每分收费各是多少
合作学习
在上面的问题中，主要等量关系是什么
6元话费 按原收费标准的通话时间＋5 　　
　　　　　 ＝ 按新收费标准的通话时间
＝
＋5
如果设原来的收费标准是 元／分，可列怎样的方程
长话费调 低了
思考
该方程与我们学过的
一元一次方程
有什么不同
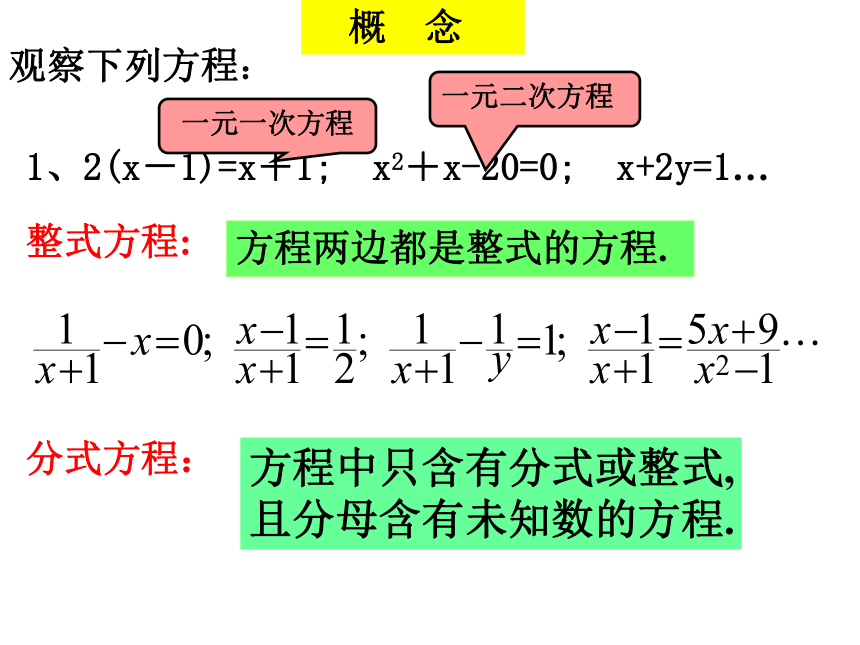
1、2(x－1)=x＋1; x2＋x-20=0; x+2y=1…
整式方程:
方程两边都是整式的方程.
分式方程：
方程中只含有分式或整式,且分母含有未知数的方程.
观察下列方程：
概 念
一元一次方程
一元二次方程
找一找：
1. 下列方程中属于分式方程的有（ ）;
① ②
③ ④ x2 +2x-1=0
① ③
巩 固 定 义
2、已知分式 ,当x
时,分式无意义.
3、分式 与 的
最简公分母是 .
X2-1≠0
x(x―3)
≠±1
2x(x―3)2
例1　解分式方程
例2　解分式方程
1．在方程的两边都乘以公分母，约去分母化成整式方程．
2．解整式方程．
3．验根．
（可代入原方程，或代入公分母。）
解方程 去分母，化为整式方程，正确的是（　　）
Ｃ
增根的定义
增根:在去分母,将分式方程转化为整式方程的过程中出现的不适合于原方程的根.
产生的原因:分式方程两边同乘以一个零因式后,所得的根是整式方程的根,而不是分式方程的根.
····
····
使分母值为零的根
······
···
必须检验
6、解下列方程：
若方程没有解，则
当m为何值时，去分母解方程：
　　　　　　　　　　会产生增根
解：两边同时乘以　　 得
把　　　代入得：
若有增根，则增根是　　
反思：分式方程产生增根，也就是使分母等于0.
将原分式方程去分母后，代入增根.
没有解.
例1 解分式方程
化简,得整式方程 2(x－1)=x＋1
解整式方程,得 x=3.
　　　把x=3代入原方程，得
左边= , 右边= .
∵ 左边=右边
∴ 原方程的根是 x=3.
● ● ● ● ●
分式方程
整式方程
解整式方程
检 验
转化
① ② ③
检验：
解分式方程
解: 方程的两边同乘以最简公分母2(x＋1),
得 2(x＋1) · ·2(x＋1)
例2 解分式方程
解 方程两边同乘以最简公分母(x＋1)(x－1),
解整式方程,得 x1=－1, x2=8
得 （x-1)2 =5x+9
x2-2x+1=5x+9
X2-7x-8=0
(x+1)(x-8)=0
解分式方程的基本思路：
去分母
整式方程
分式方程
例2 解分式方程
解 方程两边同乘以最简公分母(x＋1)(x－1),
解整式方程,得 x1=－1, x2=8
检验:把x1=－1，x2=8代入原方程
当x1=－1时, 原方程的两个分母值为零,分式无意义，因此x1=－1不是原方程的根.
当x2=8时, 左边= , 右边=
左边=右边, 因此x2=8是原方程的根.
∴ 原方程的根是x=8.
① ② ③
得 （x-1)2 =5x+9
例2 解分式方程
解 方程两边同乘以最简公分母(x＋1)(x－1),
解整式方程,得 x = 1
检验:把x = -1 代入原方程
结果使原方程的最简公分母x2-1=0 ,分式无意义，因此x = -1不是原方程的根.
∴ 原方程无解 .
① ② ③
得 （x-1)2 =5x+9
+1
+1·(x+1)(x-1)
增根
x2-2x+1=5x+9+x2-1
-7x=7
x=-1
(填空)1、解方程:
解:方程两边同乘以 ,
化简,得 .
解得 x1= , x2= .
检验:把x1= ,代入最简公分母,
x(x-2)= = ≠0;
把x2= ,代入最简公分母,
x(x-2)= =0
∴x= 是增根,舍去. ∴原方程的根是x= .
x(x-2)
x 2+ x -6=0 或x(x+1)-6=0
-3 2
-3
-3(-3-2) 15
2
2(2-2)
2
-3
练 一 练
············
·· ·······
① ② ③
2、分式方程 的最简公分母是 .
3、如果 有增根,那么增根为 .
5、若分式方程 有增根x=2,则
a= .
X=2
X-1
分析:
原分式方程去分母,两边同乘以(x2 -4),得 a(x+2)+4=0 ①
把x=2代入整式方程①,得 4a+4=0, a=-1
∴ a=-1时,x=2是原方程的增根.
-1
4、关于x的方程 =4 的解是x= ,则a= .
2
思 考:
解分式方程的验根与解一元一次、一元二次方程的验根有什么区别？
检验可有新方法
使分母为零的未知数的值,就是增根.
试说明这样检验的理由.
议一议,启迪思维
解分式方程一般需要哪几个步骤
去分母，化为整式方程：
⑴把各分母分解因式;
⑵找出各分母的最简公分母;
⑶方程两边各项乘以最简公分母;
解整式方程.
检验.
(1)把未知数的值代入原方程(一般方法);
(2)把未知数的值代入最简公分母(简便方法).
结论 ：确定分式方程的解.
想一想
1
这里的检验要以计算正确为前提
解分式方程容易犯的错误主要有：
(1)去分母时，原方程整式部分漏乘即每一项都需乘以最简公分母。
(2)约去分母后，分子是多项式时， 要注意添括号．
(3)增根不舍掉.
(4)……
想一想
2
解分式方程的一般步骤.
增根与验根.
增根及增根产生的原因.
解分式方程容易发生的错误.
在解分式方程中你有何收获与体会.
要注意灵活运用解分式方程的步骤.
同时要有简算意识,提高运算的速度和准确性.
体会数学转化的思想方法.
小结
作业，提升能力之法宝
课本p183作业题
作业题7.4（1）
祝你成功！
(填空)1、解方程:
解:方程两边同乘以最简公分母 ,
化简,得 .
解得 x1= , x2= .
x(x-2)
x 2+ x -6=0 或x(x+1)-6=0
-3 2
练 一 练
① ②
检验:把x1= ,代入最简公分母,
x(x-2)= = ≠0;
把x2= ,代入最简公分母,
x(x-2)= =0
∴x= 是增根,舍去. ∴原方程的根是x= .
-3
-3(-3-2) 15
2
2(2-2)
2
-3
练 一 练
再 见