7.4分式方程

(共15张PPT)
7、4分式方程（1）
某地电话公司调低了长途电话的话费标准，每分费用降低了25％，因此按原收费标准6元话费的通话时间，在新收费标准下可多通话5分时间，问前后两种收费标准每分收费各是多少
合作学习
在上面的问题中，主要等量关系是什么
6元话费 按原收费标准的通话时间＋5 　　 ＝ 按新收费标准的通话时间
＝
＋5
如果设原来的收费标准是 元／分，可列怎样的方程
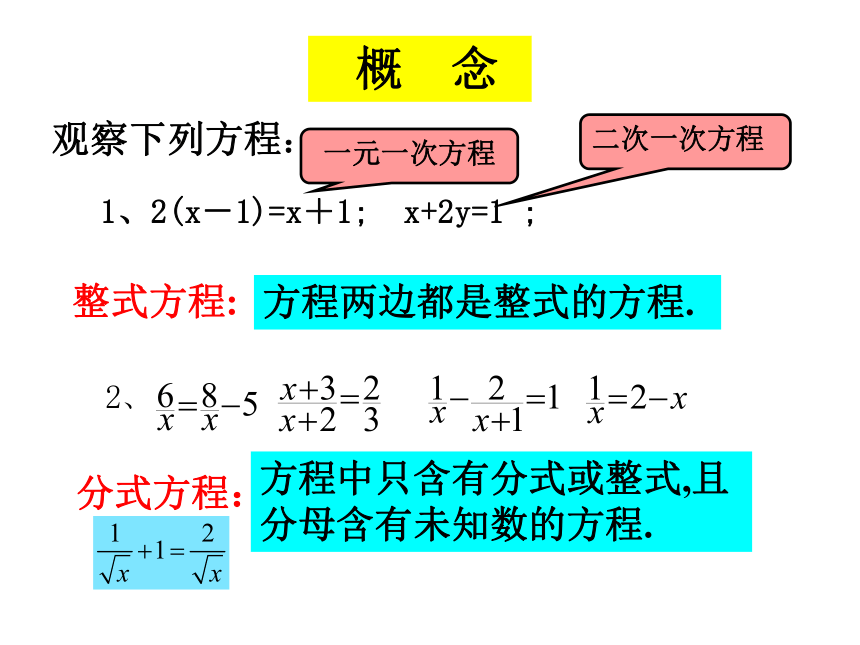
1、2(x－1)=x＋1; x+2y=1 ;
整式方程:
方程两边都是整式的方程.
分式方程：
方程中只含有分式或整式,且分母含有未知数的方程.
观察下列方程：
概 念
一元一次方程
二次一次方程
2、
找一找：
1. 下列方程中属于分式方程的有（ ）;
① ②
③ ④
③ ④
巩 固 定 义
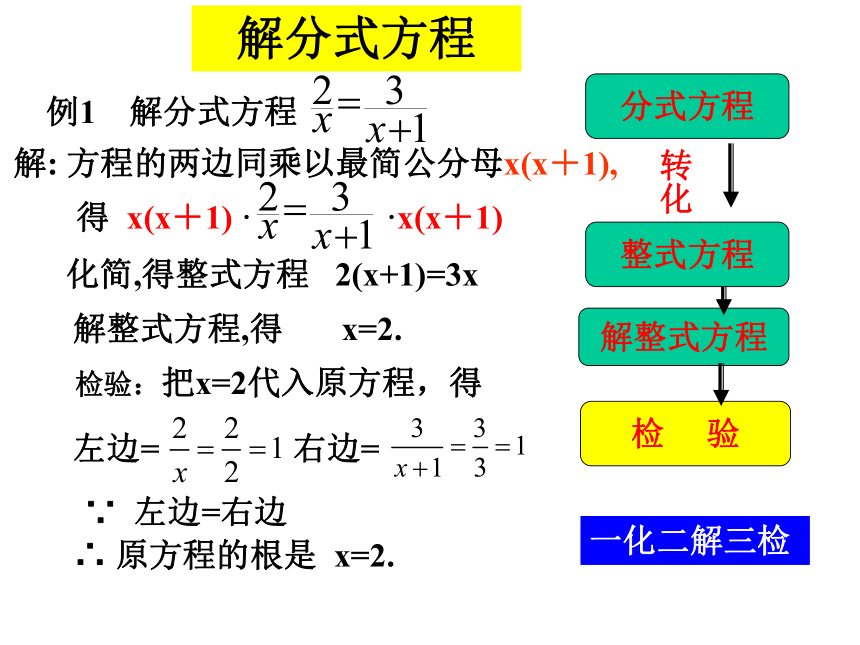
例1 解分式方程
化简,得整式方程 2(x+1)=3x
解整式方程,得 x=2.
∵ 左边=右边
∴ 原方程的根是 x=2.
分式方程
整式方程
解整式方程
检 验
转化
解分式方程
解: 方程的两边同乘以最简公分母x(x＋1),
得 x(x＋1) · ·x(x＋1)
检验：把x=2代入原方程，得
左边= 右边=
一化二解三检
你来试一试
解:方程两边同乘以最简公分母__________,
化简,得 .
解得x=______.
检验:
(x-3)
2 - x= - 1-2（x-3）
3
将x=3代入原方程，结果使原方程中分式的分母的值为0，分式没有意义，所以x=3不是原方程的根，原方程无解。
（x-3） （ ）（x-3）
增根的定义
增根:
在去分母,将分式方程转化为整式方程的过程中出现的不适合于原方程的根.
分式方程两边同乘以一个零因式后,所得的根是整式方程的根,而不是分式方程的根.
使分母值为零的根
必须检验
产生的原因:
你来试一试
解:方程两边同乘以最简公分母（x-3），
化简,得 2-x=-1-2（x-3）
解得 x=3
检验1
将x=3代入原方程，结果使原方程中分式的分母的值为0，分式没有意义，所以x=3不是原方程的根，原方程无解。
检验2
将x=1代入最简公分母：
（x-3）=0，
所以x=3是增根，舍去，
原方程无解.
尝试练习
第一组: (1) (2)
可要仔细了，每项别漏乘噢！验根可别忘记了.
第二组: (1) (2)
挑战新高
例:若关于x的方程 会产生增根,请你求出m的值
方程如果产生增根,则增根是什么呢
如果关于x的方程
有增根，
则m的值你会求吗？
解:方程两边同时乘以(x-3),
X+m=m(x-3)　　　①
∵方程有增根
∴ x=3
将x=3代入①,得m=-3.
————聪明的你肯定能采摘到丰收 的果实，收获成功的喜悦.
1、有下列方程① ， ② ③ ，
是分式方程的有（ ）
A ① ② B ② ③ C ① ③ D ② ④
2、解方程 时，下列变形正确的是 （ ）
A、3x+3-2x+1=1 B、3x+3-2x-1=1
C、3x+3-2x+1=3x D、3x+3-2x-1=3x
4、当x=_______时, 的值为4.
3、 会产生增根,则 m 的值等于( )
A、-2 B、-1 C、1 D、2
智慧园
智慧园
5、解分式方程：
6、当m为何值时，去分母解方程：
　　　　　　　　　　会产生增根
课堂小结
解分式方程一般需要哪几个步骤
(一化二解三检)
去分母，化为整式方程：
解整式方程.
检验.
结论
(1)找出各分母的最简公分母;
(2)方程两边各项乘以最简公分母;
(1)把未知数的值代入原方程(一般方法);
(2)把未知数的值代入最简公分母(简便方法).
要注意因式分解
注意每项都乘
这里的求解以正确为前提
解分式方程注意的问题
作业，提升能力之法宝
课本p183作业题
作业题7.4（1）
祝你成功
末来是属于你们的,今天的努力是为了明天飞得更高,更远,祝你们成功.