4.4二元一次方程组的应用（2）

(共28张PPT)
一根金属棒在0℃时的长度是q m,温度每升高1 ℃,它就伸长p m.当温度为t ℃时,金属棒的长度L可用公式L=pt+q计算.
已测得当t=100 ℃时, L=2.002m;
当t=500 ℃时, L=2.01m.
(1)求p,q的值;
(2)若这根金属棒加热后长度伸长到2.016m,问这时金属棒的温度是多少
L=pt+q： t=100 , L=2.002; t=500 , L=2.01.
(1)求p,q的值;
(2)若这根金属棒加热后长度伸长到2.016m,问这时金属棒的温度是多少
t=100 t=500
L=2.002 L=2.01
解 (1) 把
代入pt+q=L中，得：
100p+q=2.002 ①
500p+q=2.01 ②
② - ①得：400 p = 0.008， p=0.00002
把p=0.00002代入①,得：0.002+q=2.002，q=2
(2)由(1) 得：L=0.00002t+2
当L=2.016时，2.016=0.00002t+2，解得t=800
答：这时金属棒的温度是800℃。
讨论归纳：例2的解题步骤？
①代入（将已知的量　代入关系式）
②列（列出二元一次方程组）
③解（解这个二元一次方程组）
④回代（把求得p、q值重新回代到关系式中，使关系式只有两个相关的量，如只有L与t）
这种求字母系数的方法称为待定系数法
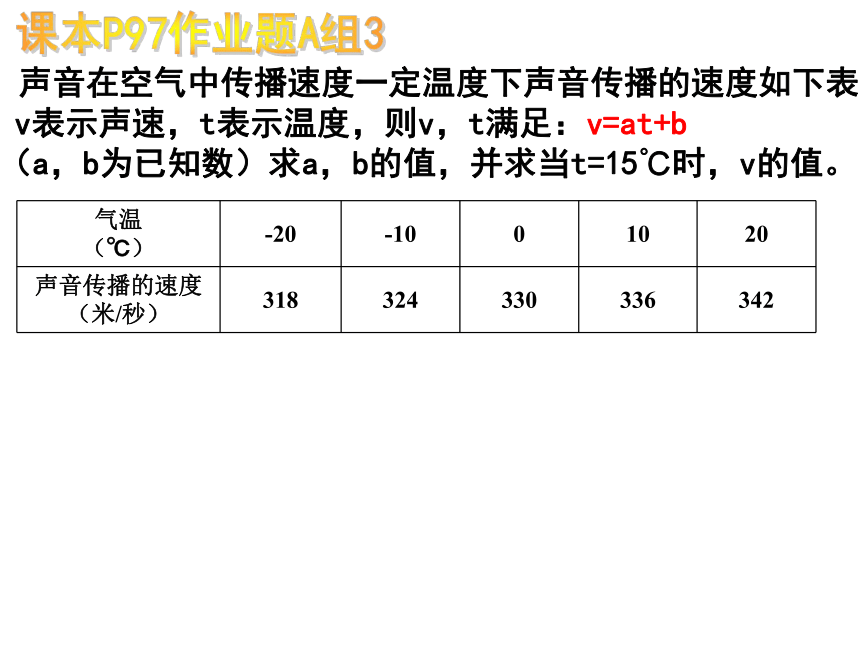
声音在空气中传播速度一定温度下声音传播的速度如下表。v表示声速，t表示温度，则v，t满足：v=at+b
（a，b为已知数）求a，b的值，并求当t=15℃时，v的值。
气温
（℃） -20 -10 0 10 20
声音传播的速度（米/秒） 318 324 330 336 342
声音在空气中传播速度一定温度下声音传播的速度如下表。v表示声速，t表示温度，则v，t满足：v=at+b
（a，b为已知数）求a，b的值，并求当t=15℃时，v的值。
解 (1) 把
t=0 t=10
v=330 v=336
当t=0℃时，v=330米/秒；当t=10℃时，v=336米/秒。
代入at+b=v中，得：
b=330 ①
10a+b=336 ②
b=330
a=0.6
解得
(2)由(1) 得：v=0.6t+330
当t=15时， v=0.6×15+330=339
答：当t=15℃时，v的值为339米/秒。
通过对一份中学生营养快餐的检测，得到以下信息：
(1)快餐总质量为300g；
(2)快餐的成分：蛋白质、碳水化合物、脂肪、矿物质；
(3)蛋白质和脂肪含量占50%；矿物质的含量是脂肪含
量的2倍；蛋白质和碳水化合物含量占85%.
根据上述数据回答下面的问题：
①分别求出营养快餐中蛋白质、碳水化合物、脂肪、
矿物质的质量和所占百分比；
②根据计算结果制作扇形统计图表示营养成分的信息。
快餐总质量为300克
蛋白质＋碳水化合物＋脂肪＋矿物质＝３００g
蛋白质和脂肪含量占50%
蛋白质＋脂肪＝３００ g × 50%
矿物质含量是脂肪含量的2倍
蛋白质和碳水化合物含量占85%
蛋白质＋碳水化合物＝ ３００g × 85%
矿物质＝２×脂肪
快餐的成分:蛋白质,碳水化合物,脂肪,矿物质
x
y
（300×85%－x）
2y
蛋白质＋脂肪＝３００ × 50%
矿物质+碳水化合物= ３００ × 50%
已知量：
蛋白质
碳水化合物
脂肪
矿物质
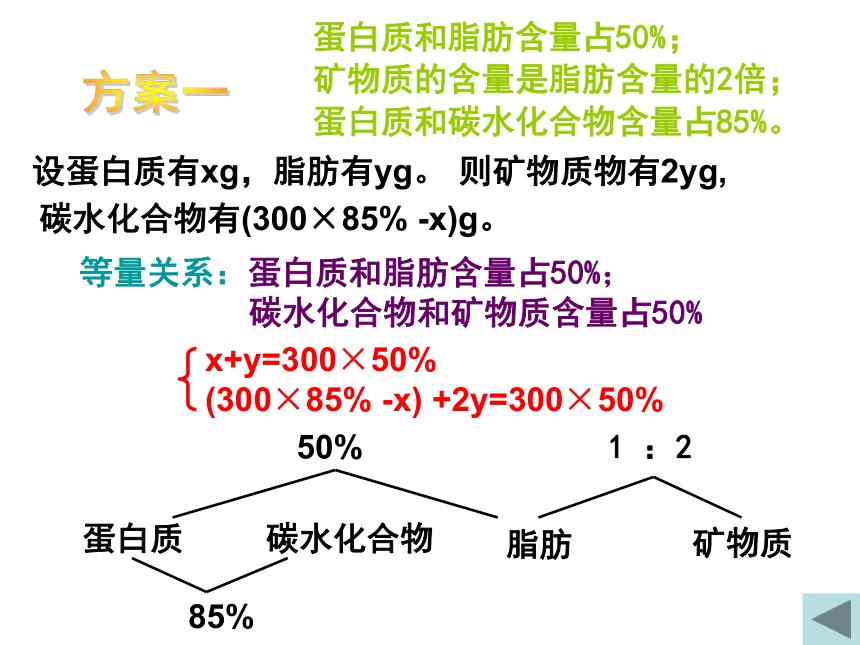
蛋白质和脂肪含量占50%；
矿物质的含量是脂肪含量的2倍；
蛋白质和碳水化合物含量占85%。
设蛋白质有xg，脂肪有yg。
则矿物质物有2yg,
碳水化合物有(300×85% -x)g。
50%
1 ：2
85%
x+y=300×50% (300×85% -x) +2y=300×50%
等量关系：蛋白质和脂肪含量占50%；
碳水化合物和矿物质含量占50%
蛋白质
碳水化合物
脂肪
矿物质
蛋白质和脂肪含量占50%；
矿物质的含量是脂肪含量的2倍；
蛋白质和碳水化合物含量占85%。
设蛋白质有xg，碳水化合物有yg。
则脂肪有(150-x)g,
矿物质有2(150-x)g。
50%
1 ：2
85%
x+y=300×85% y+2(150-x)=300×50%
等量关系：蛋白质和碳水化合物含量占85%
碳水化合物和矿物质含量占50%
蛋白质
脂肪
矿物质
碳水化合物
合计
各种成分的质量（g） 135 15 30 120 300
各种成分所占百分比
45% 5% 10% 40% 100%
中学生营养快餐成分统计表
复习
绘制扇形统计图的步骤有那些？
1、计算各部分所占的百分比
2、计算各个扇形的圆心角度数
3、在圆中画出各个扇形并标上相应的项目和百分比
4、注明统计统计图名称
10%
5%
40%
45%
回顾反思
检验所求答案是否符合题意
反思本例对我们有什么启示？
解信息量大，关系复杂的实际问题时，要仔细分析题意，找出等量关系，
利用它们的数量关系适当地设元，然后列方程组解题。
摩托车 公交车 货车 小汽车 合计
7:50~8:00 7 12 44
8:00~8:10 7 8 40
合计 30 20 20
下表是小红在2003年下旬制作的一份统计表,其中空格处的字迹已模糊不清,但小红还记得7:50~8:00时段内的摩托车辆数与8:00~8:10时段内的货车辆数之比是5:4.根据这些数据,你能把这分统计表填完整吗
2003年6月23日东胜路7:50~8:10经过车辆统计表
单位:辆
等量关系： 7:50~8:00摩托车: 8:00~8:10=5:4
摩托+公交+货车+小汽车=总辆数
x
y
20-y
摩托车 公交车 货车 小汽车 合计
7:50~8:00 25 7 0 12 44
8:00~8:10 5 7 20 8 40
合计 30 14 20 20 84
谈谈你的收获
1、如何求一些公式中的字母系数（待定系数法）它的一般步骤是怎样的？
2、怎样解决一些信息量大，关系比较复杂的实际问题？
某村有土地58公顷，计划将12公顷山坡地开辟为茶园，其余的土地种植粮食和蔬菜。已知种粮食的土地面积是种蔬菜的19/4倍，问计划种植粮食和蔬菜的土地面积各多少公顷？
等量关系：茶园+粮食+蔬菜=总土地面积；
种粮食=种蔬菜× 19/4
解：设种粮食x公顷，种蔬菜y公顷。
x+y+12 = 58
x = 19/4y
解得：
x=25
y=20
答：种粮食25公顷，种蔬菜20公顷。
1）某校教师举行茶话会，若每桌坐12人，则空出一张桌子；若每桌坐10人，还有10人不能就坐。问该校有多少名教师？共准备了多少张桌子？
等量关系：每桌人数12人×（桌数-1）=总人数；
每桌人数10人× 桌数+10人=总人数。
解：设该校有x名教师，共准备了y张桌子。
12(y-1) = x
10y + 10 = x
解得：
x=120
y=11
答：该校有120名教师，共准备了11张桌子。
2）李明家以两种储蓄方法分别存了2000元和1000元，一年后全部取出，扣除利息税后可得利息43.92元。如果这两笔钱的两种储蓄方法交换一下，一年后全部取出，扣除利息税后只能得到利息33.84元。已知利息税的税率为20%，问当时这两种储蓄的年利率各是多少？
等量关系：
本金1×时间×利率1×（1-20%）
+本金2×时间×利率2×（1-20%）=总税后利息
解：设两种储蓄方法的年利率分别是x和y。
2000x×80% + 1000y×80% = 43.92
1000x×80% + 2000y×80% = 33.84
解得：
x=2.25%
y=0.99%
答：两种储蓄方法的年利率分别是2.25%和0.99%。
120°
96°
144°
3)通过一次对某校七年级学生的问卷调查，得到如图的统计图，已知最喜爱看文艺节目的人数比最喜爱看新闻节目的人数多48人，问最喜爱看文艺节目新闻节目的各有多少人？接受问卷调查的学生共有多少人？
等量关系：文艺人数=新闻人数+48
文艺人数 120
新闻人数 96
解：设观看文艺节目的x人，新闻节目的y人。
x-y=48
x/y=120/96
解得：
x=240
y=192
总人数：240÷120/360=720人
4)一条铁路线A,B,C三个车站的位置如图所示。已知B,C两车站之间相距520千米。火车从B站出发，向C站方向匀速行驶，经过30分，距A站150千米；经过2时，距A站345千米。问火车从B站开出，多少时间后可到达C站？
A
B
C
150km
A
B
C
345km
y
经过30分
y
经过2时
y+0.5x=150
解：设火车的速度为x km/h，A,B两站的路程为y km
y+2x=345
甲乙两人分别从相距 20 千米的两地出发，相向而行。如果甲比乙早出发 30 分钟，那么在乙出发后 2 小时，他们相遇；如果他们同时出发，那么 1 小时后两人还相距 11 千米。求甲、乙每小时各走多少千米？
2y千米
甲2.5小时走的路程
乙2小时走的路程
0.5x千米
2x千米
(1)
A
B
11千米
x千米
y千米
(2)
A
B
小明骑摩托车在公路上高速行驶，12:00时看到里程碑上的数是一个两位数，它的数字之和是7；13:00时看里程碑上的两位数与12:00时看到的个位数和十位数颠倒了；14:00时看到里程碑上的数比12:00时看到的两位数中间多了个零，小明在12:00时看到里程碑上的数字是多少？
解:设小明在12:00时看到的数的十位数字是x，个位的数字是y，那么
x+y=7
(10y+x)-(10x+y)=(100x+y)-(10y+x)
答:小明在12:00时看到的数字是16.
x=1
y=6
解之:
1、某县中学生足球联赛共赛10轮(既每队均需比赛10场),其中胜一场得3分,平一场得1分,负1场得0分.向阳中学足球队在这次联赛中所负场数比踢平场数少3场,结果共得19分.向阳中学足球队在这次联赛中胜了多少场
解:设向阳中学胜x场,平y场,负z场
由题意,得 x+y+z=10
y-z=3
3x+y=19
解得 x=5
y=4
z=1
2、一批货物要运往某地,货主准备租用汽车运输公司的甲,乙两种货车.已知过去两次租用这两种货车的情况如下表:
第一次
第二次
甲种货车辆数(单位:辆)
乙种货车辆数(单位:辆)
累计运货吨数(单位:辆)
2
5
3
6
15.5
35
现租用该公司3辆甲种货车及5辆乙种货车一次刚好运完这批货,如果按每吨付运费30元计算,问:货主应付运费多少元
设甲种货车每辆运货ｘ吨，乙种货车每辆运货ｙ吨
　２ｘ+３ｙ＝１５．５　　　　　　　　　ｘ＝４
　１６０ｘ+１２００ｙ＝４８０００，解得ｙ＝２．５
3.某列车通过450米长的大桥，从车头上桥到车尾下桥共用了33秒；该车以同样的速度穿过760米长的隧道时，整个车身都在隧道内的时间为22秒，求这列车的速度和列车的长。
列车的车速 过桥时间=桥长+车长
列车的车速 过隧道时间=隧道长-车长
×
×
4.北京和上海都有某种仪器可供外地使用，其中北京可提供10台，
上海可提供4台。已知重庆需要8台，武汉需要6台，从北京、上海
将仪器运往重庆、武汉的费用如下表所示，单位：元/台
有关部门计划用7600元运送这批仪器，请你设计一种方案，使武汉、
重庆能得到所需的仪器，而且运费正好够用。
终点
起点 武 汉 重 庆
北京 400 800
上海 300 500
终点
起点 武 汉 重 庆
北京
上海
x
y
6-x
8-y