5.1同底数幂的乘法(2)

(共23张PPT)
复习回顾:
(1)74.(-7)3 (2) (-3)2.(-3)5
(3) -28.(-2)4 (4) (-a)10.(-a)11
计算下列各式，结果用幂的形式表示:
(5) –(-x)2.x3
(6) (a-b).(b-a)3(b-a)2
根据 同底数幂的乘法法则填空：
4
4
4
2
3
5
3
3
3
3
3
乘方
求几个相同因数的积的运算
x2=
x· x
=108
=a15
（其中m , n都是正整数）
试猜想探索
n个
n个
幂的乘方，底数不变，指数相乘。
底数不变
指数相乘
下式从左边到右边是怎样变化的？
幂的乘方法则
（am）n＝amn
（an）m＝anm
,
所以（am）n ＝ （an）m
与 相等吗？为什么？
n
m
底数不变
指数相乘
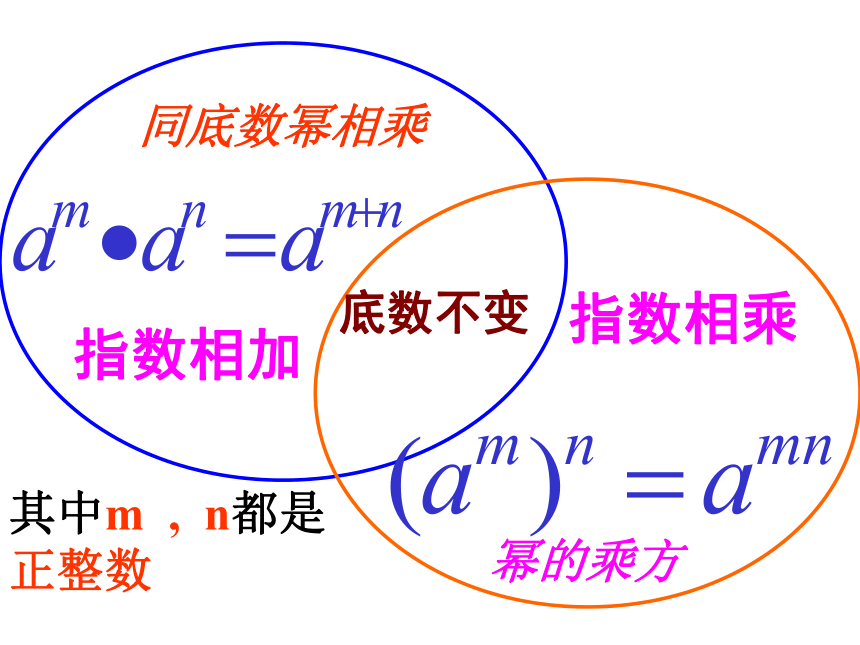
指数相加
同底数幂相乘
幂的乘方
其中m , n都是正整数
例1.计算下列各式，结果用幂的形式表示:
（107）3＝107×3＝1021
（a4）8＝a4×8＝a32
[（-x）6]3＝（-x）6×3＝（-x）18＝x18
(4)（x3）4·（x2）5
（x3）4·（x2）5＝x3×4·x2×5＝x12·x10 ＝x12＋10＝x22
下列各式对吗？请说出你的观点和理由：
(1) (a4)3=a7 ( )
(2) a4 a3=a12 ( )
(3) (a2)3+(a3)2=(a6)2 ( )
(4) (-x3)2=(-x2)3 ( )
(5) (-b3)m=(-bm)3 ( )
×
×
×
×
×
课内练习1,2,3
作业题2,5
例2 : 计算：
(3): y5· (y5)2-2 · (y5)3
作业题4
例3:幂的乘方的逆运算：
(1).1010 = ( )2 = ( )5
(2) x13·x7 =x( ) =( )5 =( )4 =( )10
(3)a2m =( )2 =( )m （m为正整数）
105
102
20
x4
x5
x2
am
a2
⑴ 85＝2（ ）
⑵ a12=(a3)( )
=(a2)( )
= a3 ·a( )
注：幂运算性质
均可逆向应用
am·an=am+n
(am) n=am n
15
4
6
9
填一填：
(3):若10a=2,10b=3, 则10a+b=____,
102a+103b=_____,102a+3b=_____
(1):an=3,则a3n=___.
(2):am=3,an=4,则am+n=____,a2m+3n=____.
1.若
2若
3.若2x+5y-3=0,则4x.32y= ____
4.若x是3的立方根,求x6的值
在255，344，433，522，这四个幂的数值中，
最大的一个是_______
344
1、若 am = 2, 则a3m =_____.
2、若 mx = 2, my = 3 ,
则 mx+y =____, m3x+2y =______.
8
6
72
1、若 a5 . (an)3 = a11，则n= ，
2、若 2n+3 = 64，则n= ，
3、已知 644×83 = 2n，则n= 。
2
3
33
(5)比较 355，444，533 的大小。
解： ∵ 355 =（35）11 = 24311
444 =（44）11 = 25611
533 =（53）11 = 12511
∴ 444 ＞355　＞ 533
⑴ a8 + (a2)4 ⑵ a3 . (a5)2
⑶ (x2 . x3)5 ⑷ (a2 . a)3 . (a2)3
⑸ (-a3)2 . a - 2a7
⑹ - ( - a2)6 – a (- a)3 . (- a2)4
计算：