乘法公式复习.ppt
图片预览




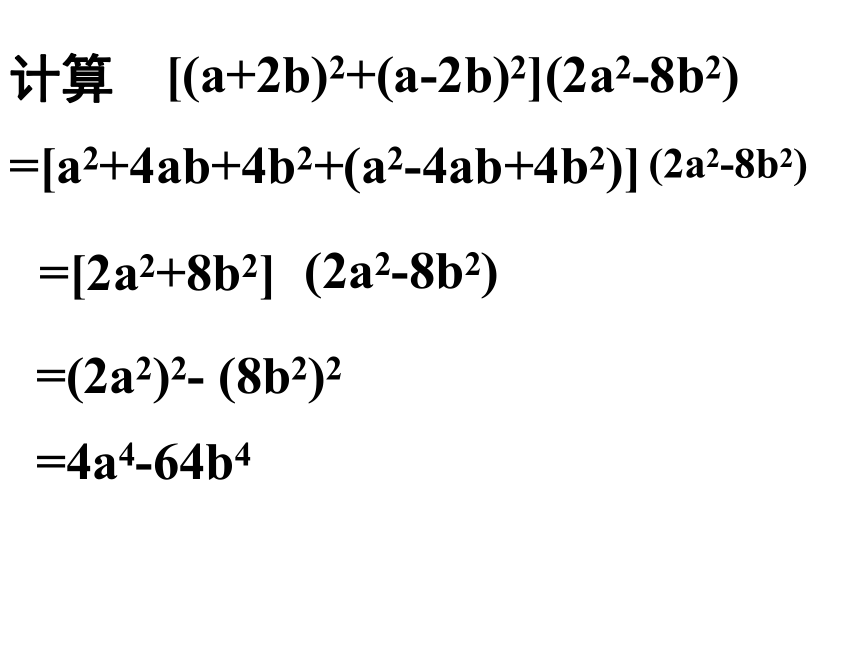


文档简介
(共18张PPT)
乘法公式
平方差公式
(a+b)(a-b)
=a2-b2
完全平方公式
(a+b)2
= a2+2ab+ b2
(a-b)2
=a2-2ab+b2
(2x+3b)(3b -2x)
=
(p+n+m)( )
=p2-(n+m)2
(-3 –2b)2
=9 -( )+4b2
x2+y2
= (x+y)2 +
9a2+( )+25b2
=(3a-5b)2
完全平方公式
(a2+
b)2
=a4+ + b2
1
4
1
2
9b2-4x2
(p-n-m)
a2b
(-2xy)
-12b
-30ab
1,下列各式:
A 、 (x+y)(-x-y);
B、(x-y)(-x-y);
C、 (2a+3b)(3b-2a)
D 、 (2X-3Y)(2Y+3X).
可以用平方差公式计算的有( );可以用 完全平方公式计算的有( )。
A
B
C
2,下列各式中,运算结果是x2-36y2的是( )
A (-6y-x)(6y-x) B(-6y+x)(6y-x)
C (x+4y)(x-9y) D (-6y+x)(-6y-x)
A
3,已知(x+a)2 =x2-8x+b,则( )
A、a=4 b=16 B、a=4 b=-16
C、a=-4 b=16 D、a=-4 b=-16
C
(1) (-x+1)(-x-1)
(2)(x+2y)2
(4)(-2a-1)2
(3) ( 2 a - 1)2
a4-(a-b)(a+b)(a2-b2)
(m+n+1)(m+n-1)-(m+n)2
计算
[(a+2b)2+(a-2b)2](2a2-8b2)
=[a2+4ab+4b2+(a2-4ab+4b2)]
(2a2-8b2)
=[2a2+8b2]
(2a2-8b2)
=(2a2)2- (8b2)2
=4a4-64b4
计算:(m-2n)2(m+2n)2(m2+4n2)2
=[(m-2n)(m+2n)]2(m2+4n2)2
= (m2-4n2)2(m2+4n2)2
=[(m2-4n2)(m2+4n2)]2
=(m4-16n4)2
=m8-32m4n4+256n8
应用一
1、请你好好想一想:
简便计算
(1)
(2)
1,若(-7m+A)(4n+B)=16n2-49m2
则 A= B=
2,a2+b2-ab+ =(a+b )2
3,(a+b)2=(a-b)2+
4,已知(a+b)2=9, (a-b)2=5 则
a2+b2= ab=
4n
7m
3ab
4ab
例:已知 a+b=3, a·b=2
求(1)a2+b2 (2)(a-b)2
解(1)a2+b2=(a+b)2-2ab
∵ a+b=3, a·b=2
∴ a2+b2=32-2×2=5
(2)(a-b)2 =(a+b)2-4ab
∵ a+b=3, a·b=2
∴(a-b)2=32-4×2=1
应用二
2、请你认真填一填
(1)已知a+b=-7,ab=10,则a2+b2=_____,ab2+a2b=_______
(2)已知(a+b)2=9,(a-b)2=25,则a2+b2=_____,ab=______.
求代数式的值
再回首
a2+b2=
ab=
(a-b)2=(a+b)2-4ab
(a+b)2=a2+b2+2ab
(a-b)2=a2+b2-2ab
(a+b)2-2ab
=(a-b)2+2ab
常用的变形公式:
(1)、如果x2+ax+121是一个完全平方式,则a的值是( )
A、11 B、±11 C、22 D、±22
2、请你仔细选一选:
应用三
求待定系数
D
若 (a+1)2+b2-8b+16=0
则 3(a-b)=
解: ∵
(a+1)2+b2-8b+16=0
∴ (a+1)2+(b -4)2=0
∴ (a+1)2=0 (b-4)2=0
∴ a= -1 b= 4
∴3(a-b)=3(-1-4)=-15
2、已知a2+b2+4a-6b+13=0,
求a2+b2的值
1、已知 ,求x3y-2x2y2+xy3的值
相信自己做一做
1, 观察下列等式,你会发现什么规律:1×3+1=22;2×4+1=32;3×5+1=42;4×6+1=52;……请你将发现的规律用仅含字母n(n为正整数)的等式表示出来:
n(n+2) +1=(n+1)2
2,计算:(2x+3y)2(2x-3y)2
3,已知﹙A+21﹚2=1512910,
求﹙A+11﹚﹙A+31﹚的值。
感悟与收获
这堂课你收获了什么?
简便计算
公式变形
求待定系数
观察下列各式:
探究活动
你能口算末位数是5的两位数的平方吗?请用完全平方公式说明理由.
乘法公式
平方差公式
(a+b)(a-b)
=a2-b2
完全平方公式
(a+b)2
= a2+2ab+ b2
(a-b)2
=a2-2ab+b2
(2x+3b)(3b -2x)
=
(p+n+m)( )
=p2-(n+m)2
(-3 –2b)2
=9 -( )+4b2
x2+y2
= (x+y)2 +
9a2+( )+25b2
=(3a-5b)2
完全平方公式
(a2+
b)2
=a4+ + b2
1
4
1
2
9b2-4x2
(p-n-m)
a2b
(-2xy)
-12b
-30ab
1,下列各式:
A 、 (x+y)(-x-y);
B、(x-y)(-x-y);
C、 (2a+3b)(3b-2a)
D 、 (2X-3Y)(2Y+3X).
可以用平方差公式计算的有( );可以用 完全平方公式计算的有( )。
A
B
C
2,下列各式中,运算结果是x2-36y2的是( )
A (-6y-x)(6y-x) B(-6y+x)(6y-x)
C (x+4y)(x-9y) D (-6y+x)(-6y-x)
A
3,已知(x+a)2 =x2-8x+b,则( )
A、a=4 b=16 B、a=4 b=-16
C、a=-4 b=16 D、a=-4 b=-16
C
(1) (-x+1)(-x-1)
(2)(x+2y)2
(4)(-2a-1)2
(3) ( 2 a - 1)2
a4-(a-b)(a+b)(a2-b2)
(m+n+1)(m+n-1)-(m+n)2
计算
[(a+2b)2+(a-2b)2](2a2-8b2)
=[a2+4ab+4b2+(a2-4ab+4b2)]
(2a2-8b2)
=[2a2+8b2]
(2a2-8b2)
=(2a2)2- (8b2)2
=4a4-64b4
计算:(m-2n)2(m+2n)2(m2+4n2)2
=[(m-2n)(m+2n)]2(m2+4n2)2
= (m2-4n2)2(m2+4n2)2
=[(m2-4n2)(m2+4n2)]2
=(m4-16n4)2
=m8-32m4n4+256n8
应用一
1、请你好好想一想:
简便计算
(1)
(2)
1,若(-7m+A)(4n+B)=16n2-49m2
则 A= B=
2,a2+b2-ab+ =(a+b )2
3,(a+b)2=(a-b)2+
4,已知(a+b)2=9, (a-b)2=5 则
a2+b2= ab=
4n
7m
3ab
4ab
例:已知 a+b=3, a·b=2
求(1)a2+b2 (2)(a-b)2
解(1)a2+b2=(a+b)2-2ab
∵ a+b=3, a·b=2
∴ a2+b2=32-2×2=5
(2)(a-b)2 =(a+b)2-4ab
∵ a+b=3, a·b=2
∴(a-b)2=32-4×2=1
应用二
2、请你认真填一填
(1)已知a+b=-7,ab=10,则a2+b2=_____,ab2+a2b=_______
(2)已知(a+b)2=9,(a-b)2=25,则a2+b2=_____,ab=______.
求代数式的值
再回首
a2+b2=
ab=
(a-b)2=(a+b)2-4ab
(a+b)2=a2+b2+2ab
(a-b)2=a2+b2-2ab
(a+b)2-2ab
=(a-b)2+2ab
常用的变形公式:
(1)、如果x2+ax+121是一个完全平方式,则a的值是( )
A、11 B、±11 C、22 D、±22
2、请你仔细选一选:
应用三
求待定系数
D
若 (a+1)2+b2-8b+16=0
则 3(a-b)=
解: ∵
(a+1)2+b2-8b+16=0
∴ (a+1)2+(b -4)2=0
∴ (a+1)2=0 (b-4)2=0
∴ a= -1 b= 4
∴3(a-b)=3(-1-4)=-15
2、已知a2+b2+4a-6b+13=0,
求a2+b2的值
1、已知 ,求x3y-2x2y2+xy3的值
相信自己做一做
1, 观察下列等式,你会发现什么规律:1×3+1=22;2×4+1=32;3×5+1=42;4×6+1=52;……请你将发现的规律用仅含字母n(n为正整数)的等式表示出来:
n(n+2) +1=(n+1)2
2,计算:(2x+3y)2(2x-3y)2
3,已知﹙A+21﹚2=1512910,
求﹙A+11﹚﹙A+31﹚的值。
感悟与收获
这堂课你收获了什么?
简便计算
公式变形
求待定系数
观察下列各式:
探究活动
你能口算末位数是5的两位数的平方吗?请用完全平方公式说明理由.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
