浙教版七年级数学下册限时训练 1.4 《平行线的性质》 (word版 含解析)
文档属性
| 名称 | 浙教版七年级数学下册限时训练 1.4 《平行线的性质》 (word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 160.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-23 00:00:00 | ||
图片预览




文档简介
浙教版七年级数学下册限时训练:1.4 《平行线的性质》
限时:50分钟 姓名________ 评价________
一.选择题
1.如图,已知直线a∥b,直线c与直线a,b分别交于点A,B.若∠1=54°,则∠2等于( )
A.126° B.134° C.136° D.144°
2.如图,已知直线a∥b,c∥b,∠1=60°,则∠2的度数是( )
A.30° B.60° C.120° D.61°
3.如图,下列说法正确的是( )
A.若AB∥CD,则∠1=∠2 B.若AD∥BC,则∠3=∠4
C.若∠1=∠2,则AB∥CD D.若∠1=∠2,则AD∥BC
4.如图,l1∥l2,点O在直线l1上,若∠AOB=90°,∠1=35°,则∠2的度数为( )
A.65° B.55° C.45° D.35°
5.将一张长方形纸片折叠成如图所示的形状,则∠EAG=( )
A.34° B.56° C.68° D.146°
6.如图,AB∥CD,AF交CD于点O,且OF平分∠EOD,如果∠A=34°,那么∠EOC的度数是( )
A.134° B.68° C.112° D.146°
7.如图:AB∥CD,CB⊥DB,∠D=55°,则∠ABC的度数是( )
A.55° B.35° C.25° D.65°
8.如图,AB∥CD∥EF,AC∥DF,∠BAC=120°,则∠F=( )
A.60° B.120° C.150° D.180°
9.如图,已知∠1=∠2,∠3=125°,∠4的度数为( )
A.45° B.55° C.65° D.75°
10.已知:如图,∠1=∠2.
试说明:∠C=∠DBA.
解∵∠1=∠2(已知),
∠1=∠DGF(对顶角相等),
∴∠2=∠DGF(等量代换),
∴BD∥CE( )
∴∠C=∠DBA( )
①两直线平行,内错角相等;②同位角相等;③内错角相等,两直线平行;④两直线平行,同位角相等;⑤同位角相等,两直线平行.以上空缺处依次所填正确的是( )
A.③④ B.④⑤ C.⑤④ D.⑤②
二.填空题
11.如图,直线a,b被直线c所截,a∥b,∠1=110°,则∠2= .
12.如图,AB∥CD,∠FGB=150°,FG平分∠EFD,则∠AEF的度数等于 °.
13.如图,四条直线中,a∥b,c∥d,已知∠1=50°,则∠2= °.
14.如图,a∥b,OA⊥OB,∠2=55°,则∠1= .
15.已知直线a∥b,将一块含30°角的直角三角板ABC按如图所示方式放置(∠BAC=30°),并且顶点A,C分别落在直线a,b上,若∠1=22°,则∠2的度数是 .
16.如图,在△ABC中,点D、E分别在AB、BC上,且DE∥AC,∠1=∠2,
(1)AF与BC的位置关系是 ;
(2)如果∠B=30°,且∠2=80°,那么∠BAC= .
三.解答题(共4小题)
17.如图,PQ⊥AB于点T,PQ⊥CD于点N,直线EF分别与AB、CD相交于点H、K,∠FHB=70°,求∠CKE的度数填空并填写理由.
因为PQ⊥AB于点T,PQ⊥CD于点N,
所以∠BTP=∠CNQ=90°
所以AB∥CD ( )
所以∠CKE= ( )
又因为 =∠BHF=70° ( )
所以∠CKE=70°.
18.如图,已知:∠1=∠2,DE⊥AC,BC⊥AC.
求证:∠B=∠3.
证明:∵DE⊥AC,BC⊥AC(已知),
∴∠AED=∠ACB=90° ( ).
∴DE∥BC( ),
∴∠2= ( ),
∠1= ( ).
又∵∠1=∠2(已知),
∴∠B=∠3(等量代换).
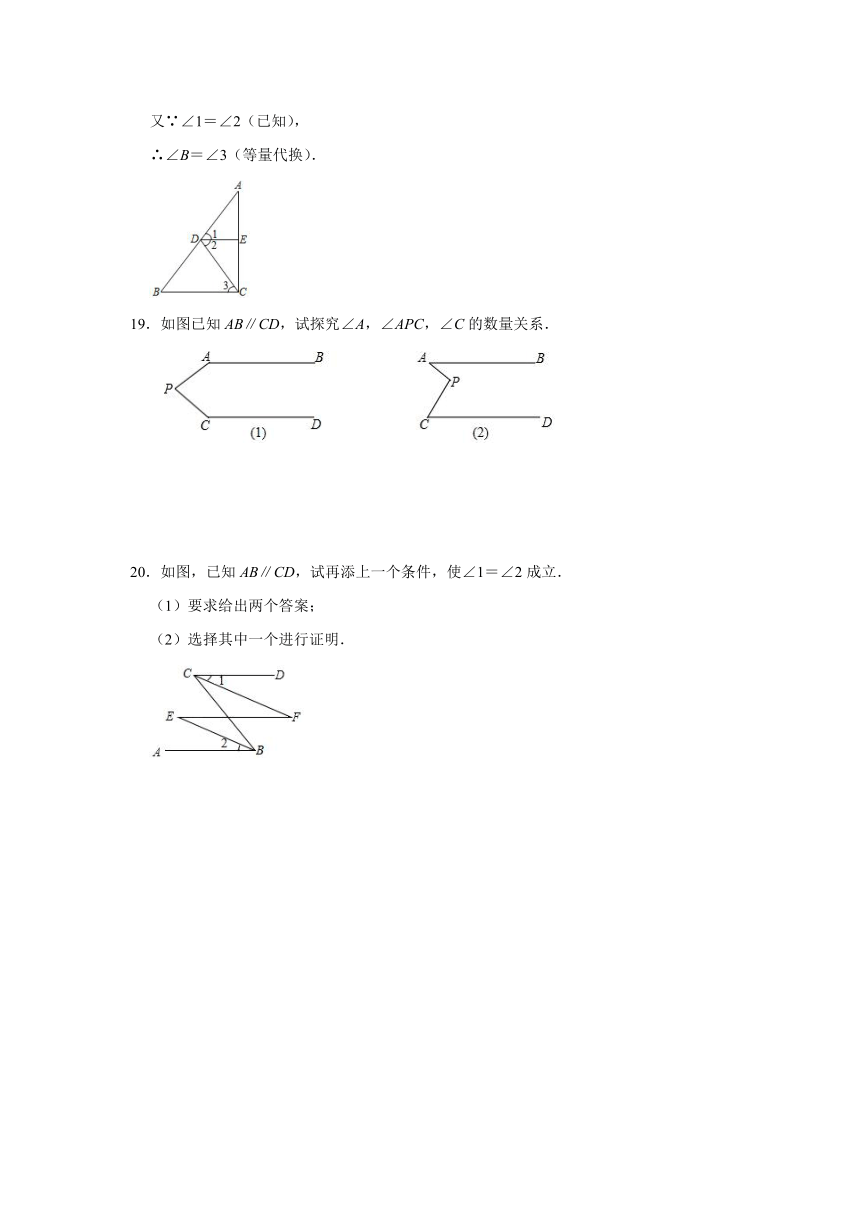
19.如图已知AB∥CD,试探究∠A,∠APC,∠C的数量关系.
20.如图,已知AB∥CD,试再添上一个条件,使∠1=∠2成立.
(1)要求给出两个答案;
(2)选择其中一个进行证明.
参考答案
一.选择题
1.解:如图所示:
∵a∥b,∠1=54°,
∴∠1=∠3=54°,
∴∠2=180°﹣54°=126°.
故选:A.
2.解:∵直线a∥b,c∥b,
∴a∥c,
∵∠1=60°,
∴∠2=∠1=60°.
故选:B.
3.解:A、若AB∥CD,则∠4=∠3,∴此选项不符合题意;
B、若AD∥BC,则∠2=∠1,∴此选项不符合题意;
C、若∠1=∠2,则AD∥BC,∴此选项不符合题意;
D、若∠1=∠2,则AD∥BC,∴此选项符合题意,
故选:D.
4.解:∵l1∥l2,∠1=35°,
∴∠OAB=∠1=35°.
∵OA⊥OB,
∴∠2=∠OBA=90°﹣∠OAB=55°.
故选:B.
5.解:∵∠CBD=34°,
∴∠ABH=∠ABC=(180°﹣34°)=73°,
∵AG∥BD,AE∥BC,
∴∠GAB=∠ABH=73°,∠BAE=180°﹣∠ABC=107°,
∴∠EAG=∠BAE﹣∠BAG=107°﹣73°=34°,
故选:A.
6.解:∵AB∥CD,∠A=34°,
∴∠DOF=∠A=34°,
∵OF平分∠EOD,
∴∠EOD=2∠FOD=68°,
∴∠EOC=180°﹣68°=112°,
故选:C.
7.解:∵CB⊥DB,
∴∠CBD=90°,
∴∠C+∠D=90°,
∵∠D=55°,
∴∠C=35°,
∵AB∥CD,
∴∠ABC=∠C=35°.
故选:B.
8.解:∵AB∥CD,∠BAC=120°,
∴∠BAC+∠ACD=180°,
∴∠ACD=60°,
∵AC∥DF,
∴∠ACD=∠CDF,
∴∠CDF=60°,
∵CD∥EF,
∴∠CDF+∠F=180°,
∴∠F=120°,
故选:B.
9.解:∵∠1=∠2,
∴l1∥l2,
∴∠4=180°﹣∠3=180°﹣125°=55°.
故选:B.
10.解:∵∠1=∠2(已知),
∠1=∠DGF(对顶角相等),
∴∠2=∠DGF(等量代换),
∴BD∥CE(同位角相等,两直线平行)
∴∠C=∠DBA(两直线平行,同位角相等)
故选:C.
二.填空题
11.解:∵a∥b,∠1=110°,
∴∠2=180°﹣110°=70°.
故答案为:70°.
12.解:∵AB∥CD,∠FGB=150°,
∴∠GFD=30°,
∵FG平分∠EFD,
∴∠EFD=60°,
∵AB∥CD,
∴∠AEF=∠EFD=60°,
故答案为:60.
13.解:∵c∥d,∠1=50°,
∴∠3=130°,
∵a∥b,
∴∠2=130°.
故答案为:130.
14.解:∵a∥b,∠2=55°,
∴∠2=∠3=55°,
∵OA⊥OB,
∴∠AOB=90°,
∵∠1+∠AOB+∠3=180°,
∴∠1=35°,
故答案为35°.
15.解:如图,过点B作BD∥a,
∴∠ABD=∠1=22°,
∵a∥b,
∴BD∥b,
∴∠2=∠DBC=∠ABC﹣∠ABD=60°﹣22°=38°.
故答案为:38°.
16.解:(1)∵DE∥AC,
∴∠2=∠C,
∵∠1=∠2,
∴∠1=∠C,
∴AF∥BC;
(2)∵AF∥BC,
∴∠B+∠BAF=180°,
∴∠BAF=180°﹣30°=150°,
∵∠1=∠2=80°,
∴∠BAC=150°﹣80°=70°.
故答案为平行;70°.
三.解答题(共4小题)
17.解:∵PQ⊥AB于点T,PQ⊥CD于点N,
∴∠BTP=∠CNQ=90°,
∴AB∥CD (内错角相等,两直线平行),
∴∠CKE=∠AHE(两直线平行,同位角相等),
∵∠AHE=∠BHF=70° (对顶角相等),
∴∠CKE=70°.
故答案为:内错角相等,两直线平行;∠AHE;两直线平行,同位角相等;∠AHE;对顶角相等.
18.证明:∵DE⊥AC,BC⊥AC(已知),
∴∠AED=∠ACB=90° (垂直的定义或垂线的定义),
∴DE∥BC (同位角相等,两直线平行),
∴∠2=∠3(两直线平行,内错角相等),
∠1=∠B(两直线平行,同位角相等),
又∵∠1=∠2(已知),
∴∠B=∠3(等量代换 ).
故答案为:垂直的定义或垂线的定义;同位角相等,两直线平行;∠3;两直线平行,内错角相等;∠2;已知.
19.解:(1)过P作m∥AB,
∵AB∥CD,
∴m∥CD,
∴∠1+∠A=180°,∠2+∠C=180°,
∴∠1+∠2+∠A+∠C=360°,
∴∠A+∠C+∠APC=360°.
(2)延长CP交AB于点N,
∵AB∥CD,
∴∠C=∠ANP,
∵∠APN+∠A=∠APC,
∴∠A+∠C=∠APC.
20.解:添加∠FCB=∠CBE或CF∥BE或∠E=∠F,使∠1=∠2成立.
已知AB∥CD,CF∥BE.
求证:∠1=∠2.
证明:∵AB∥CD,
∴∠DCB=∠ABC,
∵CF∥BE,
∴∠FCB=∠CBE,
∴∠DCB﹣∠FCB=∠ABC﹣∠CBE,
即∠1=∠2.
限时:50分钟 姓名________ 评价________
一.选择题
1.如图,已知直线a∥b,直线c与直线a,b分别交于点A,B.若∠1=54°,则∠2等于( )
A.126° B.134° C.136° D.144°
2.如图,已知直线a∥b,c∥b,∠1=60°,则∠2的度数是( )
A.30° B.60° C.120° D.61°
3.如图,下列说法正确的是( )
A.若AB∥CD,则∠1=∠2 B.若AD∥BC,则∠3=∠4
C.若∠1=∠2,则AB∥CD D.若∠1=∠2,则AD∥BC
4.如图,l1∥l2,点O在直线l1上,若∠AOB=90°,∠1=35°,则∠2的度数为( )
A.65° B.55° C.45° D.35°
5.将一张长方形纸片折叠成如图所示的形状,则∠EAG=( )
A.34° B.56° C.68° D.146°
6.如图,AB∥CD,AF交CD于点O,且OF平分∠EOD,如果∠A=34°,那么∠EOC的度数是( )
A.134° B.68° C.112° D.146°
7.如图:AB∥CD,CB⊥DB,∠D=55°,则∠ABC的度数是( )
A.55° B.35° C.25° D.65°
8.如图,AB∥CD∥EF,AC∥DF,∠BAC=120°,则∠F=( )
A.60° B.120° C.150° D.180°
9.如图,已知∠1=∠2,∠3=125°,∠4的度数为( )
A.45° B.55° C.65° D.75°
10.已知:如图,∠1=∠2.
试说明:∠C=∠DBA.
解∵∠1=∠2(已知),
∠1=∠DGF(对顶角相等),
∴∠2=∠DGF(等量代换),
∴BD∥CE( )
∴∠C=∠DBA( )
①两直线平行,内错角相等;②同位角相等;③内错角相等,两直线平行;④两直线平行,同位角相等;⑤同位角相等,两直线平行.以上空缺处依次所填正确的是( )
A.③④ B.④⑤ C.⑤④ D.⑤②
二.填空题
11.如图,直线a,b被直线c所截,a∥b,∠1=110°,则∠2= .
12.如图,AB∥CD,∠FGB=150°,FG平分∠EFD,则∠AEF的度数等于 °.
13.如图,四条直线中,a∥b,c∥d,已知∠1=50°,则∠2= °.
14.如图,a∥b,OA⊥OB,∠2=55°,则∠1= .
15.已知直线a∥b,将一块含30°角的直角三角板ABC按如图所示方式放置(∠BAC=30°),并且顶点A,C分别落在直线a,b上,若∠1=22°,则∠2的度数是 .
16.如图,在△ABC中,点D、E分别在AB、BC上,且DE∥AC,∠1=∠2,
(1)AF与BC的位置关系是 ;
(2)如果∠B=30°,且∠2=80°,那么∠BAC= .
三.解答题(共4小题)
17.如图,PQ⊥AB于点T,PQ⊥CD于点N,直线EF分别与AB、CD相交于点H、K,∠FHB=70°,求∠CKE的度数填空并填写理由.
因为PQ⊥AB于点T,PQ⊥CD于点N,
所以∠BTP=∠CNQ=90°
所以AB∥CD ( )
所以∠CKE= ( )
又因为 =∠BHF=70° ( )
所以∠CKE=70°.
18.如图,已知:∠1=∠2,DE⊥AC,BC⊥AC.
求证:∠B=∠3.
证明:∵DE⊥AC,BC⊥AC(已知),
∴∠AED=∠ACB=90° ( ).
∴DE∥BC( ),
∴∠2= ( ),
∠1= ( ).
又∵∠1=∠2(已知),
∴∠B=∠3(等量代换).
19.如图已知AB∥CD,试探究∠A,∠APC,∠C的数量关系.
20.如图,已知AB∥CD,试再添上一个条件,使∠1=∠2成立.
(1)要求给出两个答案;
(2)选择其中一个进行证明.
参考答案
一.选择题
1.解:如图所示:
∵a∥b,∠1=54°,
∴∠1=∠3=54°,
∴∠2=180°﹣54°=126°.
故选:A.
2.解:∵直线a∥b,c∥b,
∴a∥c,
∵∠1=60°,
∴∠2=∠1=60°.
故选:B.
3.解:A、若AB∥CD,则∠4=∠3,∴此选项不符合题意;
B、若AD∥BC,则∠2=∠1,∴此选项不符合题意;
C、若∠1=∠2,则AD∥BC,∴此选项不符合题意;
D、若∠1=∠2,则AD∥BC,∴此选项符合题意,
故选:D.
4.解:∵l1∥l2,∠1=35°,
∴∠OAB=∠1=35°.
∵OA⊥OB,
∴∠2=∠OBA=90°﹣∠OAB=55°.
故选:B.
5.解:∵∠CBD=34°,
∴∠ABH=∠ABC=(180°﹣34°)=73°,
∵AG∥BD,AE∥BC,
∴∠GAB=∠ABH=73°,∠BAE=180°﹣∠ABC=107°,
∴∠EAG=∠BAE﹣∠BAG=107°﹣73°=34°,
故选:A.
6.解:∵AB∥CD,∠A=34°,
∴∠DOF=∠A=34°,
∵OF平分∠EOD,
∴∠EOD=2∠FOD=68°,
∴∠EOC=180°﹣68°=112°,
故选:C.
7.解:∵CB⊥DB,
∴∠CBD=90°,
∴∠C+∠D=90°,
∵∠D=55°,
∴∠C=35°,
∵AB∥CD,
∴∠ABC=∠C=35°.
故选:B.
8.解:∵AB∥CD,∠BAC=120°,
∴∠BAC+∠ACD=180°,
∴∠ACD=60°,
∵AC∥DF,
∴∠ACD=∠CDF,
∴∠CDF=60°,
∵CD∥EF,
∴∠CDF+∠F=180°,
∴∠F=120°,
故选:B.
9.解:∵∠1=∠2,
∴l1∥l2,
∴∠4=180°﹣∠3=180°﹣125°=55°.
故选:B.
10.解:∵∠1=∠2(已知),
∠1=∠DGF(对顶角相等),
∴∠2=∠DGF(等量代换),
∴BD∥CE(同位角相等,两直线平行)
∴∠C=∠DBA(两直线平行,同位角相等)
故选:C.
二.填空题
11.解:∵a∥b,∠1=110°,
∴∠2=180°﹣110°=70°.
故答案为:70°.
12.解:∵AB∥CD,∠FGB=150°,
∴∠GFD=30°,
∵FG平分∠EFD,
∴∠EFD=60°,
∵AB∥CD,
∴∠AEF=∠EFD=60°,
故答案为:60.
13.解:∵c∥d,∠1=50°,
∴∠3=130°,
∵a∥b,
∴∠2=130°.
故答案为:130.
14.解:∵a∥b,∠2=55°,
∴∠2=∠3=55°,
∵OA⊥OB,
∴∠AOB=90°,
∵∠1+∠AOB+∠3=180°,
∴∠1=35°,
故答案为35°.
15.解:如图,过点B作BD∥a,
∴∠ABD=∠1=22°,
∵a∥b,
∴BD∥b,
∴∠2=∠DBC=∠ABC﹣∠ABD=60°﹣22°=38°.
故答案为:38°.
16.解:(1)∵DE∥AC,
∴∠2=∠C,
∵∠1=∠2,
∴∠1=∠C,
∴AF∥BC;
(2)∵AF∥BC,
∴∠B+∠BAF=180°,
∴∠BAF=180°﹣30°=150°,
∵∠1=∠2=80°,
∴∠BAC=150°﹣80°=70°.
故答案为平行;70°.
三.解答题(共4小题)
17.解:∵PQ⊥AB于点T,PQ⊥CD于点N,
∴∠BTP=∠CNQ=90°,
∴AB∥CD (内错角相等,两直线平行),
∴∠CKE=∠AHE(两直线平行,同位角相等),
∵∠AHE=∠BHF=70° (对顶角相等),
∴∠CKE=70°.
故答案为:内错角相等,两直线平行;∠AHE;两直线平行,同位角相等;∠AHE;对顶角相等.
18.证明:∵DE⊥AC,BC⊥AC(已知),
∴∠AED=∠ACB=90° (垂直的定义或垂线的定义),
∴DE∥BC (同位角相等,两直线平行),
∴∠2=∠3(两直线平行,内错角相等),
∠1=∠B(两直线平行,同位角相等),
又∵∠1=∠2(已知),
∴∠B=∠3(等量代换 ).
故答案为:垂直的定义或垂线的定义;同位角相等,两直线平行;∠3;两直线平行,内错角相等;∠2;已知.
19.解:(1)过P作m∥AB,
∵AB∥CD,
∴m∥CD,
∴∠1+∠A=180°,∠2+∠C=180°,
∴∠1+∠2+∠A+∠C=360°,
∴∠A+∠C+∠APC=360°.
(2)延长CP交AB于点N,
∵AB∥CD,
∴∠C=∠ANP,
∵∠APN+∠A=∠APC,
∴∠A+∠C=∠APC.
20.解:添加∠FCB=∠CBE或CF∥BE或∠E=∠F,使∠1=∠2成立.
已知AB∥CD,CF∥BE.
求证:∠1=∠2.
证明:∵AB∥CD,
∴∠DCB=∠ABC,
∵CF∥BE,
∴∠FCB=∠CBE,
∴∠DCB﹣∠FCB=∠ABC﹣∠CBE,
即∠1=∠2.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
