初中数学浙教版七年级下册第一章1.3平行线的判定寒假预习练习题(Word版 含解析)
文档属性
| 名称 | 初中数学浙教版七年级下册第一章1.3平行线的判定寒假预习练习题(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 180.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-29 00:00:00 | ||
图片预览




文档简介
初中数学浙教版七年级下册第一章1.3平行线的判定寒假预习练习题
一、选择题
如图所示,下列条件中能判定直线的是?
A.
B.
C.
D.
如图,,要使,则的大小是
A.
B.
C.
D.
如图是嘉淇证明“在同一平面内,垂直于同一条直线的两条直线平行”的过程,下列判断不正确的是
A.
代表
B.
代表
C.
代表
D.
代表两直线平行,同位角相等
如图,可以判定的条件是
A.
B.
C.
D.
如图,给出了过直线外一点作已知直线的平行线的方法,其依据是
A.
同位角相等,两直线平行
B.
内错角相等,两直线平行
C.
旁内角互补,两直线平行
D.
两点确定一条直线
如图,直线a,b被直线c,d所截.下列条件能判定的是
A.
B.
C.
D.
下列说法正确的个数有
同位角相等;过一点有且只有一条直线与已知直线垂直;
过一点有且只有一条直线与已知直线平行;若,,则.
A.
1个
B.
2个
C.
3个
D.
4个
如图,能判定的条件是
A.
B.
C.
D.
如图,点A在BE的延长线上,点D在CF的延长线上,下列条件:,,,其中能判断的是
A.
B.
C.
D.
如图,下列条件不能判断直线的是
A.
B.
C.
D.
二、填空题
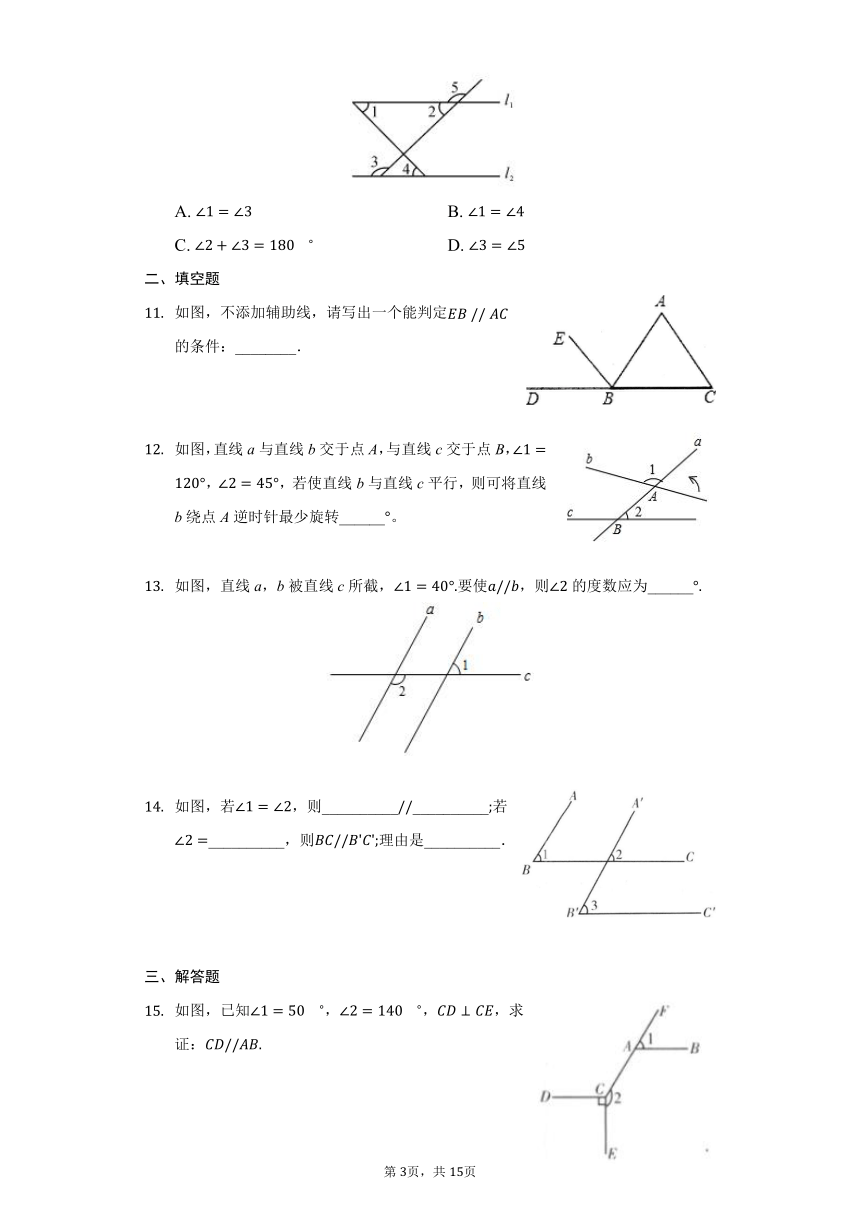
如图,不添加辅助线,请写出一个能判定的条件:________.
如图,直线a与直线b交于点A,与直线c交于点B,,,若使直线b与直线c平行,则可将直线b绕点A逆时针最少旋转______。
如图,直线a,b被直线c所截,要使,则的度数应为______
如图,若,则____________________若__________,则理由是__________.
三、解答题
如图,已知,,,求证:
如下图,已知,,,与BD平行吗与平行吗请说明理由.
如图,中,,BD平分,CE平分,BD,CE交于点O,F,G分别是AC,BC延长线上一点,且,,指出图中一组平行线,并说明理由.
如图所示,直线AB和CD与直线MN分别交于点E,点F.
如图,EG平分,FH平分分别平分了一对同旁内角,则与满足________时,;
如图,EG平分,FH平分分别平分了一对同位角,则与满足________时,;
如图,EG平分,FH平分分别平分了一对内错角,则与满足什么条件时,?请说明理由.
答案和解析
1.【答案】C
【解析】
【分析】
本题考查了平行线的判定的应用,注意:平行线的判定定理有:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
平行线的判定定理有:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
根据以上内容判断即可.
【解答】
解:根据不能推出,故A选项错误;
B.,,
,
即根据不能推出,故B选项错误;
C.,
,故C选项正确;
D.根据不能推出,故D选项错误,
故选C.
2.【答案】D
【解析】解:如果,
那么.
所以要使,则的大小是.
故选:D.
根据同位角相等,两直线平行即可求解.
本题考查的是平行线的判定定理,掌握同位角相等,两直线平行是解题的关键.
3.【答案】D
【解析】
【分析】
本题考查了平行线的判定,根据垂直的定义,得出,根据同位角相等,两直线平行,得出结论.
【解答】
已知,,,
求证:,
证明:,
垂直的定义,
已知,
垂直的定义,
等量代换,
同位角相等,两直线平行,
代表;代表;代表?
;代表同位角相等,两直线平行;
故D不正确,
故选D.
4.【答案】B
【解析】解:A、由,可得到,故此选项不合题意;
B、由,可得到,故此选项符合题意;
C、由,可得到,故此选项不合题意;
D、由,可得到,故此选项不合题意;
故选:B.
依据平行线的判定方法进行判断:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
本题主要考查了平行线的判定,同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
5.【答案】A
【解析】解:如图:
画,根据同位角相等,两直线平行可得到过直线外一点与已知直线平行的直线.
故选:A.
根据画图的方法,利用了同位角相等,两直线平行作已知直线的平行线.
本题考查了平行线判断:同位角相等,两直线平行;同旁内角互补,两直线平行;内错角相等,两直线平行.也考查了基本作图.
6.【答案】D
【解析】解:A、当时,,故此选项不合题意;
B、当时,,故此选项不合题意;
C、当时,,故此选项不合题意;
D、当时,,故此选项符合题意;
故选:D.
直接利用平行线的判定方法进而分析得出答案.
此题主要考查了平行线的判定,正确掌握判定方法是解题关键.
7.【答案】A
【解析】
【试题解析】
【分析】本题考查了同位角、垂线的性质和平行公理,是基础知识,需要熟练掌握.熟练掌握各定理或推论成立的条件是解决此题的关键.根据同位角、垂线的性质和平行公理对各个说法分析判断后即可求解.
【解答】解:如图,直线AB、CD被直线GH所截,与是同位角,但它们不相等,故说法错误;
根据垂线的性质,应该加上前提:在同一平面内,故说法错误;
应为过直线外一点有且只有一条直线与已知直线平行,故说法错误;
平行于同一直线的两条直线平行,是平行公理的推论,故说法正确.
综上所述,正确的说法是共1个.
故选:A.
8.【答案】D
【解析】
【分析】本题考查了平行线的判定,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
在复杂的图形中具有相等关系的两角首先要判断它们是否是同位角或内错角,被判断平行的两直线是否由“三线八角”而产生的被截直线,再根据平行线的判定定理解答.
【解答】解:A、不能判断出,故本选项错误;
B、不能判断出,故本选项错误;
C、只能判断出,不能判断出,故本选项错误;
D、,根据内错角相等,两直线平行,可以得出,故本选项正确.
故选:D.
9.【答案】B
【解析】
【分析】
本题考查的是平行线的判定,关键是掌握同位角相等,两直线平行.内错角相等,两直线平行.同旁内角互补,两直线平行.直接根据平行线的判定定理对各条件进行逐一分析即可.
【解答】
解:如图,
,,故本选项正确;
,,故本选项错误;
,,故本选项正确,
所以能判断的是.
故选B.
?
10.【答案】A
【解析】
【分析】
此题主要考查了平行线的判定,关键是掌握平行线的判定定理.根据平行线的判定定理:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行分别进行分析即可.
【解答】
解:不能判断直线,故此选项符合题意;
B.根据内错角相等,两直线平行可判断直线,故此选项不合题意;
C.根据同旁内角互补,两直线平行可判断直线,故此选项不合题意;
D.根据同位角相等,两直线平行可判断直线,故此选项不合题意;
故选A.
11.【答案】或或
【解析】
【分析】
解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.本题是一道探索性条件开放性题目,能有效地培养“执果索因”的思维方式与能力.本题考查平行线的判定方法.
平行线判定方法一:同位角相等,两直线平行;
平行线判定方法二:内错角相等,两直线平行;
平行线判定方法三:同旁内角互补,两直线平行.
与是内错角,如果这两个角相等,则两直线平行;
与是同位角,如果这两个角相等,则两直线平行;
与EBC是同旁内角,如果这两个角互补,两直线平行.
【解答】
解:与是内错角,如果这两个角相等,则两直线平行;
与是同位角,如果这两个角相等,则两直线平行;
与EBC是同旁内角,如果这两个角互补,两直线平行.
故答案为或或.
12.【答案】15
【解析】
【分析】
本题考查了平行线的判定:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行;两条直线都和第三条直线平行,那么这两条直线平行.先根据邻补角的定义得到,根据平行线的判定当b与a的夹角为时,,由此得到直线b绕点A逆时针旋转.
【解答】
解:,
,
,
当时,,
直线b绕点A逆时针旋转.
故答案为:15.
13.【答案】140
【解析】解:,
,
.
故答案为:140.
根据和的是邻补角可求,再根据两直线平行,同位角相等可得.
本题主要考查了平行线的判定与性质,解题时注意:两直线平行,同位角相等.
14.【答案】AB;;;同位角相等,两直线平行
【解析】
【分析】
本题主要考查了平行线的判定,解答此类要判定两直线平行的题目时,可围绕截线找同位角、内错角和同旁内角.根据平行线的判定定理即可得解.
【解答】
解:,
.
若,
则,
理由是同位角相等,两直线平行.
故答案为AB;;;同位角相等,两直线平行.
15.【答案】证明:,
,
又,
,
又且,
,
,
.
【解析】本题主要考查平行线的判定,掌握平行线的判定和性质是解题的关键,即同位角相等两直线平行,内错角相等两直线平行,同旁内角互补两直线平行,,.
由条件结合垂直的定义可求得,由可求得,可得到,可判定.
16.【答案】解:;理由如下:
,,
,
;
;理由如下:
,,
,
,
,,
,
.
【解析】此题考查平行线的判断,解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.已知,,,,故可按同位角相等两直线平行判断、.
17.【答案】解:或,
理由:,
又,
,
.
或,BD平分,CE平分,
,
又,
,
,
又,
,
;
,,
.
【解析】本题主要考查了平行线的判定定理,角平分线的定义,补角的性质根据同角的补角相等证明是关键根据同角的补角相等,和平行线的判定定理即可作出判断.
18.【答案】解:;
;
时,,
理由如下:
平分,FH平分,
,,
,
,
.
【解析】
【分析】
此题考查了平行线的判定,角平分线的定义,掌握平行线的判定及角平分线的定义是关键.
根据角平分线定义得出,,时,求出,根据平行线的判定推出即可
根据角平分线定义得出,,求出,根据平行线的判定推出即可
根据角平分线定义得出,,求出,根据平行线的判定即可得到答案.
【解答】
解:平分,FH平分,
,,
,
,
,
故答案为;
平分,FH平分,
,,
,
,
,
故答案为;
见答案.
第2页,共15页
第1页,共15页
一、选择题
如图所示,下列条件中能判定直线的是?
A.
B.
C.
D.
如图,,要使,则的大小是
A.
B.
C.
D.
如图是嘉淇证明“在同一平面内,垂直于同一条直线的两条直线平行”的过程,下列判断不正确的是
A.
代表
B.
代表
C.
代表
D.
代表两直线平行,同位角相等
如图,可以判定的条件是
A.
B.
C.
D.
如图,给出了过直线外一点作已知直线的平行线的方法,其依据是
A.
同位角相等,两直线平行
B.
内错角相等,两直线平行
C.
旁内角互补,两直线平行
D.
两点确定一条直线
如图,直线a,b被直线c,d所截.下列条件能判定的是
A.
B.
C.
D.
下列说法正确的个数有
同位角相等;过一点有且只有一条直线与已知直线垂直;
过一点有且只有一条直线与已知直线平行;若,,则.
A.
1个
B.
2个
C.
3个
D.
4个
如图,能判定的条件是
A.
B.
C.
D.
如图,点A在BE的延长线上,点D在CF的延长线上,下列条件:,,,其中能判断的是
A.
B.
C.
D.
如图,下列条件不能判断直线的是
A.
B.
C.
D.
二、填空题
如图,不添加辅助线,请写出一个能判定的条件:________.
如图,直线a与直线b交于点A,与直线c交于点B,,,若使直线b与直线c平行,则可将直线b绕点A逆时针最少旋转______。
如图,直线a,b被直线c所截,要使,则的度数应为______
如图,若,则____________________若__________,则理由是__________.
三、解答题
如图,已知,,,求证:
如下图,已知,,,与BD平行吗与平行吗请说明理由.
如图,中,,BD平分,CE平分,BD,CE交于点O,F,G分别是AC,BC延长线上一点,且,,指出图中一组平行线,并说明理由.
如图所示,直线AB和CD与直线MN分别交于点E,点F.
如图,EG平分,FH平分分别平分了一对同旁内角,则与满足________时,;
如图,EG平分,FH平分分别平分了一对同位角,则与满足________时,;
如图,EG平分,FH平分分别平分了一对内错角,则与满足什么条件时,?请说明理由.
答案和解析
1.【答案】C
【解析】
【分析】
本题考查了平行线的判定的应用,注意:平行线的判定定理有:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
平行线的判定定理有:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
根据以上内容判断即可.
【解答】
解:根据不能推出,故A选项错误;
B.,,
,
即根据不能推出,故B选项错误;
C.,
,故C选项正确;
D.根据不能推出,故D选项错误,
故选C.
2.【答案】D
【解析】解:如果,
那么.
所以要使,则的大小是.
故选:D.
根据同位角相等,两直线平行即可求解.
本题考查的是平行线的判定定理,掌握同位角相等,两直线平行是解题的关键.
3.【答案】D
【解析】
【分析】
本题考查了平行线的判定,根据垂直的定义,得出,根据同位角相等,两直线平行,得出结论.
【解答】
已知,,,
求证:,
证明:,
垂直的定义,
已知,
垂直的定义,
等量代换,
同位角相等,两直线平行,
代表;代表;代表?
;代表同位角相等,两直线平行;
故D不正确,
故选D.
4.【答案】B
【解析】解:A、由,可得到,故此选项不合题意;
B、由,可得到,故此选项符合题意;
C、由,可得到,故此选项不合题意;
D、由,可得到,故此选项不合题意;
故选:B.
依据平行线的判定方法进行判断:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
本题主要考查了平行线的判定,同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
5.【答案】A
【解析】解:如图:
画,根据同位角相等,两直线平行可得到过直线外一点与已知直线平行的直线.
故选:A.
根据画图的方法,利用了同位角相等,两直线平行作已知直线的平行线.
本题考查了平行线判断:同位角相等,两直线平行;同旁内角互补,两直线平行;内错角相等,两直线平行.也考查了基本作图.
6.【答案】D
【解析】解:A、当时,,故此选项不合题意;
B、当时,,故此选项不合题意;
C、当时,,故此选项不合题意;
D、当时,,故此选项符合题意;
故选:D.
直接利用平行线的判定方法进而分析得出答案.
此题主要考查了平行线的判定,正确掌握判定方法是解题关键.
7.【答案】A
【解析】
【试题解析】
【分析】本题考查了同位角、垂线的性质和平行公理,是基础知识,需要熟练掌握.熟练掌握各定理或推论成立的条件是解决此题的关键.根据同位角、垂线的性质和平行公理对各个说法分析判断后即可求解.
【解答】解:如图,直线AB、CD被直线GH所截,与是同位角,但它们不相等,故说法错误;
根据垂线的性质,应该加上前提:在同一平面内,故说法错误;
应为过直线外一点有且只有一条直线与已知直线平行,故说法错误;
平行于同一直线的两条直线平行,是平行公理的推论,故说法正确.
综上所述,正确的说法是共1个.
故选:A.
8.【答案】D
【解析】
【分析】本题考查了平行线的判定,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
在复杂的图形中具有相等关系的两角首先要判断它们是否是同位角或内错角,被判断平行的两直线是否由“三线八角”而产生的被截直线,再根据平行线的判定定理解答.
【解答】解:A、不能判断出,故本选项错误;
B、不能判断出,故本选项错误;
C、只能判断出,不能判断出,故本选项错误;
D、,根据内错角相等,两直线平行,可以得出,故本选项正确.
故选:D.
9.【答案】B
【解析】
【分析】
本题考查的是平行线的判定,关键是掌握同位角相等,两直线平行.内错角相等,两直线平行.同旁内角互补,两直线平行.直接根据平行线的判定定理对各条件进行逐一分析即可.
【解答】
解:如图,
,,故本选项正确;
,,故本选项错误;
,,故本选项正确,
所以能判断的是.
故选B.
?
10.【答案】A
【解析】
【分析】
此题主要考查了平行线的判定,关键是掌握平行线的判定定理.根据平行线的判定定理:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行分别进行分析即可.
【解答】
解:不能判断直线,故此选项符合题意;
B.根据内错角相等,两直线平行可判断直线,故此选项不合题意;
C.根据同旁内角互补,两直线平行可判断直线,故此选项不合题意;
D.根据同位角相等,两直线平行可判断直线,故此选项不合题意;
故选A.
11.【答案】或或
【解析】
【分析】
解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.本题是一道探索性条件开放性题目,能有效地培养“执果索因”的思维方式与能力.本题考查平行线的判定方法.
平行线判定方法一:同位角相等,两直线平行;
平行线判定方法二:内错角相等,两直线平行;
平行线判定方法三:同旁内角互补,两直线平行.
与是内错角,如果这两个角相等,则两直线平行;
与是同位角,如果这两个角相等,则两直线平行;
与EBC是同旁内角,如果这两个角互补,两直线平行.
【解答】
解:与是内错角,如果这两个角相等,则两直线平行;
与是同位角,如果这两个角相等,则两直线平行;
与EBC是同旁内角,如果这两个角互补,两直线平行.
故答案为或或.
12.【答案】15
【解析】
【分析】
本题考查了平行线的判定:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行;两条直线都和第三条直线平行,那么这两条直线平行.先根据邻补角的定义得到,根据平行线的判定当b与a的夹角为时,,由此得到直线b绕点A逆时针旋转.
【解答】
解:,
,
,
当时,,
直线b绕点A逆时针旋转.
故答案为:15.
13.【答案】140
【解析】解:,
,
.
故答案为:140.
根据和的是邻补角可求,再根据两直线平行,同位角相等可得.
本题主要考查了平行线的判定与性质,解题时注意:两直线平行,同位角相等.
14.【答案】AB;;;同位角相等,两直线平行
【解析】
【分析】
本题主要考查了平行线的判定,解答此类要判定两直线平行的题目时,可围绕截线找同位角、内错角和同旁内角.根据平行线的判定定理即可得解.
【解答】
解:,
.
若,
则,
理由是同位角相等,两直线平行.
故答案为AB;;;同位角相等,两直线平行.
15.【答案】证明:,
,
又,
,
又且,
,
,
.
【解析】本题主要考查平行线的判定,掌握平行线的判定和性质是解题的关键,即同位角相等两直线平行,内错角相等两直线平行,同旁内角互补两直线平行,,.
由条件结合垂直的定义可求得,由可求得,可得到,可判定.
16.【答案】解:;理由如下:
,,
,
;
;理由如下:
,,
,
,
,,
,
.
【解析】此题考查平行线的判断,解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.已知,,,,故可按同位角相等两直线平行判断、.
17.【答案】解:或,
理由:,
又,
,
.
或,BD平分,CE平分,
,
又,
,
,
又,
,
;
,,
.
【解析】本题主要考查了平行线的判定定理,角平分线的定义,补角的性质根据同角的补角相等证明是关键根据同角的补角相等,和平行线的判定定理即可作出判断.
18.【答案】解:;
;
时,,
理由如下:
平分,FH平分,
,,
,
,
.
【解析】
【分析】
此题考查了平行线的判定,角平分线的定义,掌握平行线的判定及角平分线的定义是关键.
根据角平分线定义得出,,时,求出,根据平行线的判定推出即可
根据角平分线定义得出,,求出,根据平行线的判定推出即可
根据角平分线定义得出,,求出,根据平行线的判定即可得到答案.
【解答】
解:平分,FH平分,
,,
,
,
,
故答案为;
平分,FH平分,
,,
,
,
,
故答案为;
见答案.
第2页,共15页
第1页,共15页
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
