2021年浙教版七年级数学下册同步练习:1.4平行线的性质 (Word版 含解析)
文档属性
| 名称 | 2021年浙教版七年级数学下册同步练习:1.4平行线的性质 (Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 103.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-31 10:47:44 | ||
图片预览




文档简介
2021年浙教版七年级数学下册同步练习
1.4平行线的性质
一.选择题
1.如图,AB∥CD,∠1=105°,则∠2的度数是( )
A.65°
B.75°
C.85°
D.105°
2.如图,平行线AB,CD被直线AE所截,∠1=75°,则∠2的度数( )
A.105°
B.115°
C.125°
D.135°
3.如图,一块直角三角尺的一个顶点落在直尺的一边上,若∠2=35°,则∠1的度数为( )
A.45°
B.55°
C.65°
D.75°
4.如图,已知AB∥CD,直线l分别交AB、CD于点E、F,若∠EFD=40°,则∠BEF的度数是( )
A.40°
B.100°
C.130°
D.140°
5.如图,直线a∥b,点B在a上,且AB⊥BC.若∠1=35°,那么∠2等于( )
A.45°
B.50°
C.55°
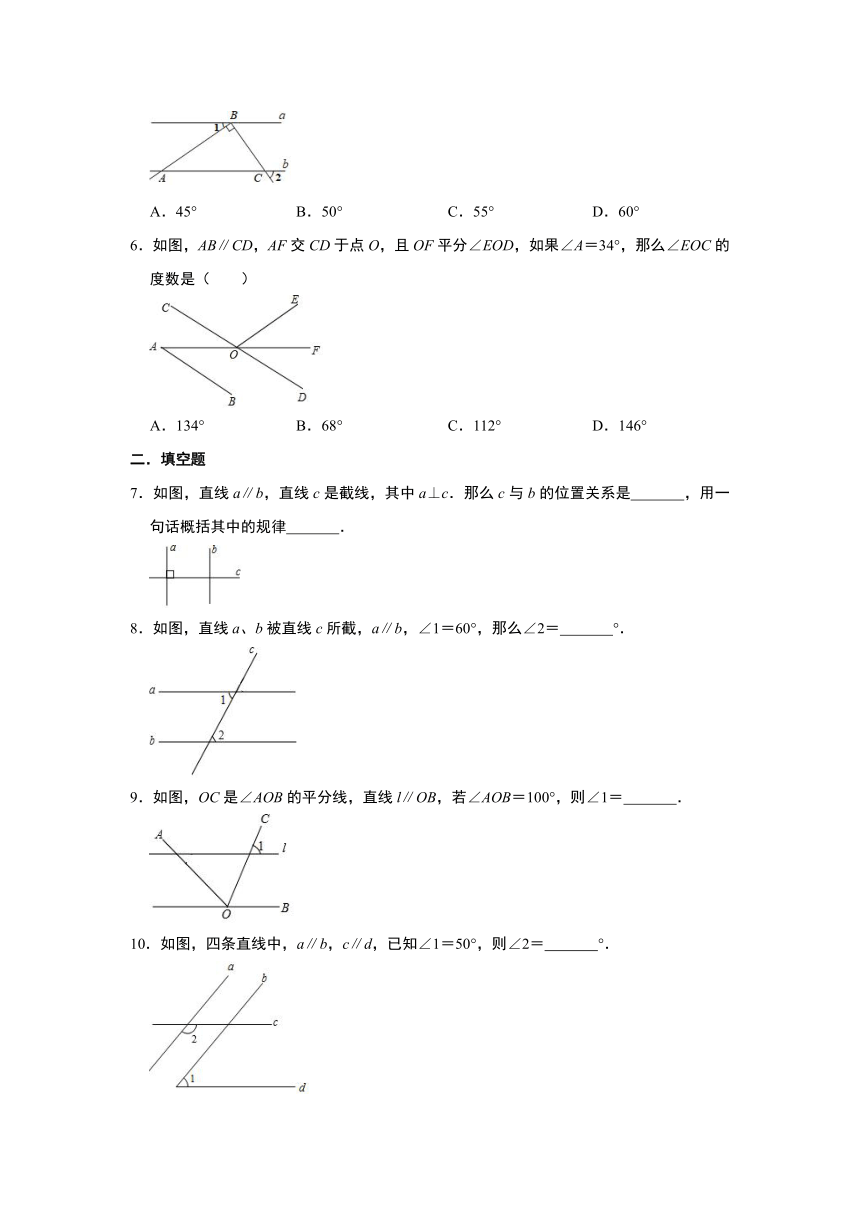
D.60°
6.如图,AB∥CD,AF交CD于点O,且OF平分∠EOD,如果∠A=34°,那么∠EOC的度数是( )
A.134°
B.68°
C.112°
D.146°
二.填空题
7.如图,直线a∥b,直线c是截线,其中a⊥c.那么c与b的位置关系是
,用一句话概括其中的规律
.
8.如图,直线a、b被直线c所截,a∥b,∠1=60°,那么∠2=
°.
9.如图,OC是∠AOB的平分线,直线l∥OB,若∠AOB=100°,则∠1=
.
10.如图,四条直线中,a∥b,c∥d,已知∠1=50°,则∠2=
°.
11.如图,∠1=35°,∠2=35°,∠3=56°23′,则∠4的大小为
.
12.如图,已知l1∥l2,∠C=90°,∠1=40°,则∠2的度数是
.
三.解答题
13.如图,EF∥AD,∠BEF=∠ADG,∠BAC=80°,求∠AGD的度数.
14.如图,AO∥CD,OB∥DE,∠O=40°,求∠D的度数.
(1)请完成下列书写过程.
∵AO∥CD(已知)
∴∠O=
=40°(
)
又∵OB∥DE(已知)
∴
=∠1=
°(
)
(2)若在平面内取一点M,作射线MP∥OA,MQ∥OB,则∠PMQ=
°.
15.直线AB、CD交于点O,OE为∠BOD的平分线,OF⊥OE,CG∥OE,且∠C=30°.
(1)求∠AOE为多少度;
(2)判断∠FOA与∠FOD的大小关系,并说明理由.
16.如图,已知∠1+∠2=180°,∠3=∠B,判断∠AED与∠C的大小关系.阅读下面的解答过程,填空并填写理由.
解:∵∠1+∠2=180°(已知),
∠1+∠4=180°(邻补角定义),
∴∠2=∠4
(
).
∴AB∥EF(
).
∴∠3=(
).
又∵∠3=∠B(已知),
∴(
)=∠B(等量代换).
∴DE∥BC(
).
∴∠AED=∠C(
).
17.已知EF⊥BC,∠1=∠C,∠2+∠3=180°.
证明:(1)GD∥AC;
(2)∠ADC=90°.
18.如图①,直线l1∥l2,直线EF和直线l1、l2分别交于C、D两点,点A、B分别在直线l1、l2上,点P在直线EF上,连结PA、PB.
猜想:如图①,若点P在线段CD上,∠PAC=15°,∠PBD=40°,则∠APB的大小为
度.
探究:如图①,若点P在线段CD上,直接写出∠PAC、∠APB、∠PBD之间的数量关系.
拓展:如图②,若点P在射线CE上或在射线DF上时,直接写出∠PAC、∠APB、∠PBD之间的数量关系.
参考答案
一.选择题
1.解:∵AB∥CD,
∴∠2+∠2=180°,
∵∠1=105°,
∴∠2=180°﹣105°=75°.
故选:B.
2.解:∵∠1=75°,
∴∠AED=∠1=75°,
∵AB∥CD,
∴∠2+∠AED=180°,
∴∠2=180°﹣75°=105°,
故选:A.
3.解:如图,
作EF∥AB,
∵AB∥CD,
∴EF∥AB∥CD,
∴∠2=∠AEF=35°,∠1=∠FEC,
∵∠AEC=90°,
∴∠1=90°﹣35°=55°,
故选:B.
4.解:∵AB∥CD,∠EFD=40°,
∴∠BEF=180°﹣40°=140°,
故选:D.
5.解:∵a∥b,∠1=35°,
∴∠BAC=∠1=35°.
∵AB⊥BC,
∴∠2=∠BCA=90°﹣∠BAC=55°.
故选:C.
6.解:∵AB∥CD,∠A=34°,
∴∠DOF=∠A=34°,
∵OF平分∠EOD,
∴∠EOD=2∠FOD=68°,
∴∠EOC=180°﹣68°=112°,
故选:C.
二.填空题
7.解:∵a∥b,
∴∠1=∠2,
∵a⊥C,
∴∠1=90°,
∴∠2=90°,
∴b⊥c,
故答案为b⊥c;用一句话概括其中的规律:两条平行线被直线所截,如果其中一条平行线与截线垂直,则另一条平行线也与截线垂直.
8.解:∵a∥b,
∴∠2=∠1=60°.
故答案为:60°.
9.解:∵OC是∠AOB的平分线,
∴∠COB=∠AOB=100°=50°,
∵直线l∥OB,
∴∠1=∠COB=50°,
故答案为:50°.
10.解:∵c∥d,∠1=50°,
∴∠3=130°,
∵a∥b,
∴∠2=130°.
故答案为:130.
11.解:如图,
∵∠1=35°,∠2=35°,
∴∠1=∠2,
∴a∥b,
∴∠4=∠5,
∵∠3=56°23′,
∴∠5=180°﹣∠3=123°37′,
∴∠4=123°37′.
故答案为:123°37′.
12.解:如图,过点C作直线l,使l∥l1∥l2,则∠1=∠3,∠2=∠4.
∵∠3+∠4=90,∠1=40°,
∴∠2=90°﹣40°=50°.
故答案是:50°.
三.解答题
13.解:∵EF∥AD(已知)
∴∠2=∠3,
又∵∠1=∠2(已知),
∴∠1=∠3,
∴AB∥DG,
∴∠BAC+∠AGD=180°,
∵∠BAC=80°(已知),
∴∠AGD=100°.
14.解:(1)∵AO∥CD(已知),
∴∠O=∠1=40°(两直线平行,同位角相等),
又∵OB∥DE(已知),
∴∠D=∠1=40°(两直线平行,同位角相等).
故答案为:∠1,两直线平行,同位角相等,∠D,40°,两直线平行,同位角相等;
(2)若在平面内取一点M,作射线MP∥OA,MQ∥OB,则∠PMQ=(40或140)°.
故答案为:(40或140).
15.解:(1)∵CG∥OE,
∴∠DOE=∠C=30°,
∵OE为∠BOD的平分线,
∴∠BOE=∠DOE=30°,
∴∠AOE=180°﹣30°=150°;
(2)∠AOF=∠DOF,
理由:∵∠BOE=∠DOE=30°,
∴∠AOD=120°,
∵OF⊥OE,
∴∠EOF=90°,
∴∠DOF=60°,
∴∠AOF=60°,
∴∠AOF=∠DOF.
16.解:∵∠1+∠2=180°(已知),
∠1+∠4=180°(邻补角定义),
∴∠2=∠4
(同角的补角相等).
∴AB∥EF(内错角相等,两直线平行).
∴∠3=∠ADE.
又∵∠3=∠B(已知),
∴∠ADE=∠B(等量代换).
∴DE∥BC(同位角相等,两直线平行).
∴∠AED=∠C(两直线平行,同位角相等)
故答案为:同角的补角相等,内错角相等,两直线平行;∠ADE,∠ADE,同位角相等,两直线平行;两直线平行,同位角相等.
17.证明:(1)∵∠1=∠C,
∴GD∥AC(同位角相等,两直线平行);
(2)由(1)知,GD∥AC,
则∠2=∠DAC,
∵∠2+∠3=180°,
∴∠DAC+∠3=180°,
∴AD∥EF,
∴∠ADC=∠EFC,
∵EF⊥BC,
∴∠EFC=90°,
∴∠ADC=90°.
18.解:猜想:如图①,过点P作PG∥l1,
∵l1∥l2,
∴l1∥l2∥PG,
∴∠APG=∠PAC=15°,∠BPG=∠PBD=40°,
∴∠APB=∠APG+∠BPG=∠PAC+∠PBD=15°+40°=55°,
∴∠APB的大小为55度,
故答案为:55;
探究:如图①,∠PAC=∠APB﹣∠PBD,理由如下:
∵l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠APB=∠APG+∠BPG=∠PAC+∠PBD,
∴∠PAC=∠APB﹣∠PBD;
拓展:∠PAC=∠PBD﹣∠APB或∠PAC=∠APB+∠PBD,理由如下:
如图,当点P在射线CE上时,
过点P作PG∥l1,
∴l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠PAC=∠APG=∠BPG﹣∠APB,
∴∠PAC=∠PBD﹣∠APB;
当点P在射线DF上时,
过点P作PG∥l1,
∴l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠PAC=∠APG=∠APB+∠BPG,
∴∠PAC=∠APB+∠PBD,
综上所述:当点P在射线CE上或在射线DF上时,∠PAC=∠PBD﹣∠APB或∠PAC=∠APB+∠PBD.
1.4平行线的性质
一.选择题
1.如图,AB∥CD,∠1=105°,则∠2的度数是( )
A.65°
B.75°
C.85°
D.105°
2.如图,平行线AB,CD被直线AE所截,∠1=75°,则∠2的度数( )
A.105°
B.115°
C.125°
D.135°
3.如图,一块直角三角尺的一个顶点落在直尺的一边上,若∠2=35°,则∠1的度数为( )
A.45°
B.55°
C.65°
D.75°
4.如图,已知AB∥CD,直线l分别交AB、CD于点E、F,若∠EFD=40°,则∠BEF的度数是( )
A.40°
B.100°
C.130°
D.140°
5.如图,直线a∥b,点B在a上,且AB⊥BC.若∠1=35°,那么∠2等于( )
A.45°
B.50°
C.55°
D.60°
6.如图,AB∥CD,AF交CD于点O,且OF平分∠EOD,如果∠A=34°,那么∠EOC的度数是( )
A.134°
B.68°
C.112°
D.146°
二.填空题
7.如图,直线a∥b,直线c是截线,其中a⊥c.那么c与b的位置关系是
,用一句话概括其中的规律
.
8.如图,直线a、b被直线c所截,a∥b,∠1=60°,那么∠2=
°.
9.如图,OC是∠AOB的平分线,直线l∥OB,若∠AOB=100°,则∠1=
.
10.如图,四条直线中,a∥b,c∥d,已知∠1=50°,则∠2=
°.
11.如图,∠1=35°,∠2=35°,∠3=56°23′,则∠4的大小为
.
12.如图,已知l1∥l2,∠C=90°,∠1=40°,则∠2的度数是
.
三.解答题
13.如图,EF∥AD,∠BEF=∠ADG,∠BAC=80°,求∠AGD的度数.
14.如图,AO∥CD,OB∥DE,∠O=40°,求∠D的度数.
(1)请完成下列书写过程.
∵AO∥CD(已知)
∴∠O=
=40°(
)
又∵OB∥DE(已知)
∴
=∠1=
°(
)
(2)若在平面内取一点M,作射线MP∥OA,MQ∥OB,则∠PMQ=
°.
15.直线AB、CD交于点O,OE为∠BOD的平分线,OF⊥OE,CG∥OE,且∠C=30°.
(1)求∠AOE为多少度;
(2)判断∠FOA与∠FOD的大小关系,并说明理由.
16.如图,已知∠1+∠2=180°,∠3=∠B,判断∠AED与∠C的大小关系.阅读下面的解答过程,填空并填写理由.
解:∵∠1+∠2=180°(已知),
∠1+∠4=180°(邻补角定义),
∴∠2=∠4
(
).
∴AB∥EF(
).
∴∠3=(
).
又∵∠3=∠B(已知),
∴(
)=∠B(等量代换).
∴DE∥BC(
).
∴∠AED=∠C(
).
17.已知EF⊥BC,∠1=∠C,∠2+∠3=180°.
证明:(1)GD∥AC;
(2)∠ADC=90°.
18.如图①,直线l1∥l2,直线EF和直线l1、l2分别交于C、D两点,点A、B分别在直线l1、l2上,点P在直线EF上,连结PA、PB.
猜想:如图①,若点P在线段CD上,∠PAC=15°,∠PBD=40°,则∠APB的大小为
度.
探究:如图①,若点P在线段CD上,直接写出∠PAC、∠APB、∠PBD之间的数量关系.
拓展:如图②,若点P在射线CE上或在射线DF上时,直接写出∠PAC、∠APB、∠PBD之间的数量关系.
参考答案
一.选择题
1.解:∵AB∥CD,
∴∠2+∠2=180°,
∵∠1=105°,
∴∠2=180°﹣105°=75°.
故选:B.
2.解:∵∠1=75°,
∴∠AED=∠1=75°,
∵AB∥CD,
∴∠2+∠AED=180°,
∴∠2=180°﹣75°=105°,
故选:A.
3.解:如图,
作EF∥AB,
∵AB∥CD,
∴EF∥AB∥CD,
∴∠2=∠AEF=35°,∠1=∠FEC,
∵∠AEC=90°,
∴∠1=90°﹣35°=55°,
故选:B.
4.解:∵AB∥CD,∠EFD=40°,
∴∠BEF=180°﹣40°=140°,
故选:D.
5.解:∵a∥b,∠1=35°,
∴∠BAC=∠1=35°.
∵AB⊥BC,
∴∠2=∠BCA=90°﹣∠BAC=55°.
故选:C.
6.解:∵AB∥CD,∠A=34°,
∴∠DOF=∠A=34°,
∵OF平分∠EOD,
∴∠EOD=2∠FOD=68°,
∴∠EOC=180°﹣68°=112°,
故选:C.
二.填空题
7.解:∵a∥b,
∴∠1=∠2,
∵a⊥C,
∴∠1=90°,
∴∠2=90°,
∴b⊥c,
故答案为b⊥c;用一句话概括其中的规律:两条平行线被直线所截,如果其中一条平行线与截线垂直,则另一条平行线也与截线垂直.
8.解:∵a∥b,
∴∠2=∠1=60°.
故答案为:60°.
9.解:∵OC是∠AOB的平分线,
∴∠COB=∠AOB=100°=50°,
∵直线l∥OB,
∴∠1=∠COB=50°,
故答案为:50°.
10.解:∵c∥d,∠1=50°,
∴∠3=130°,
∵a∥b,
∴∠2=130°.
故答案为:130.
11.解:如图,
∵∠1=35°,∠2=35°,
∴∠1=∠2,
∴a∥b,
∴∠4=∠5,
∵∠3=56°23′,
∴∠5=180°﹣∠3=123°37′,
∴∠4=123°37′.
故答案为:123°37′.
12.解:如图,过点C作直线l,使l∥l1∥l2,则∠1=∠3,∠2=∠4.
∵∠3+∠4=90,∠1=40°,
∴∠2=90°﹣40°=50°.
故答案是:50°.
三.解答题
13.解:∵EF∥AD(已知)
∴∠2=∠3,
又∵∠1=∠2(已知),
∴∠1=∠3,
∴AB∥DG,
∴∠BAC+∠AGD=180°,
∵∠BAC=80°(已知),
∴∠AGD=100°.
14.解:(1)∵AO∥CD(已知),
∴∠O=∠1=40°(两直线平行,同位角相等),
又∵OB∥DE(已知),
∴∠D=∠1=40°(两直线平行,同位角相等).
故答案为:∠1,两直线平行,同位角相等,∠D,40°,两直线平行,同位角相等;
(2)若在平面内取一点M,作射线MP∥OA,MQ∥OB,则∠PMQ=(40或140)°.
故答案为:(40或140).
15.解:(1)∵CG∥OE,
∴∠DOE=∠C=30°,
∵OE为∠BOD的平分线,
∴∠BOE=∠DOE=30°,
∴∠AOE=180°﹣30°=150°;
(2)∠AOF=∠DOF,
理由:∵∠BOE=∠DOE=30°,
∴∠AOD=120°,
∵OF⊥OE,
∴∠EOF=90°,
∴∠DOF=60°,
∴∠AOF=60°,
∴∠AOF=∠DOF.
16.解:∵∠1+∠2=180°(已知),
∠1+∠4=180°(邻补角定义),
∴∠2=∠4
(同角的补角相等).
∴AB∥EF(内错角相等,两直线平行).
∴∠3=∠ADE.
又∵∠3=∠B(已知),
∴∠ADE=∠B(等量代换).
∴DE∥BC(同位角相等,两直线平行).
∴∠AED=∠C(两直线平行,同位角相等)
故答案为:同角的补角相等,内错角相等,两直线平行;∠ADE,∠ADE,同位角相等,两直线平行;两直线平行,同位角相等.
17.证明:(1)∵∠1=∠C,
∴GD∥AC(同位角相等,两直线平行);
(2)由(1)知,GD∥AC,
则∠2=∠DAC,
∵∠2+∠3=180°,
∴∠DAC+∠3=180°,
∴AD∥EF,
∴∠ADC=∠EFC,
∵EF⊥BC,
∴∠EFC=90°,
∴∠ADC=90°.
18.解:猜想:如图①,过点P作PG∥l1,
∵l1∥l2,
∴l1∥l2∥PG,
∴∠APG=∠PAC=15°,∠BPG=∠PBD=40°,
∴∠APB=∠APG+∠BPG=∠PAC+∠PBD=15°+40°=55°,
∴∠APB的大小为55度,
故答案为:55;
探究:如图①,∠PAC=∠APB﹣∠PBD,理由如下:
∵l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠APB=∠APG+∠BPG=∠PAC+∠PBD,
∴∠PAC=∠APB﹣∠PBD;
拓展:∠PAC=∠PBD﹣∠APB或∠PAC=∠APB+∠PBD,理由如下:
如图,当点P在射线CE上时,
过点P作PG∥l1,
∴l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠PAC=∠APG=∠BPG﹣∠APB,
∴∠PAC=∠PBD﹣∠APB;
当点P在射线DF上时,
过点P作PG∥l1,
∴l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠PAC=∠APG=∠APB+∠BPG,
∴∠PAC=∠APB+∠PBD,
综上所述:当点P在射线CE上或在射线DF上时,∠PAC=∠PBD﹣∠APB或∠PAC=∠APB+∠PBD.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
