浙教版数学七年级下册1.4《平行线的性质》同步练习(word含答案)
文档属性
| 名称 | 浙教版数学七年级下册1.4《平行线的性质》同步练习(word含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 180.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-01 19:10:09 | ||
图片预览

文档简介
浙教版数学七年级下册1.4《平行线的性质》
同步练习
一、选择题
1.如图,l1∥l2,∠1=56°,则∠2的度数为(
)
A.34°
B.56°
C.124°
D.146°
2.如图,一条公路两次转弯后又回到原来的方向,若第一次转弯时∠B=140°,则∠C的度数(
)
A.140°
B.40°
C.100°
D.180°
3.如图,直线m∥n,点A在直线m上,点B,C在直线n上,AB=BC,∠1=70°,CD⊥AB于D,那么∠2等于(
)
A.20°
B.30°
C.32°
D.25°
4.下面四个图形中,∠1=∠2一定成立的是(
)
5.如图,AB∥CD∥EF,BC∥AD,AC平分∠BAD,则图中与∠AGE相等的角(
)
A.2个
B.3个
C.4个
D.5个
6.如图,已知AB∥CD,BC平分∠ABE,∠C=33°,则∠CEF的度数是(
)
A.16°
B.33°
C.49°
D.66°
7.如图,已知a∥b,三角形直角顶点在直线a上,已知∠1=25°18/27//,则∠2度数是(
)
A.25°18/27//
B.640
41/33//
C.74°4133//
D.64°41/43//
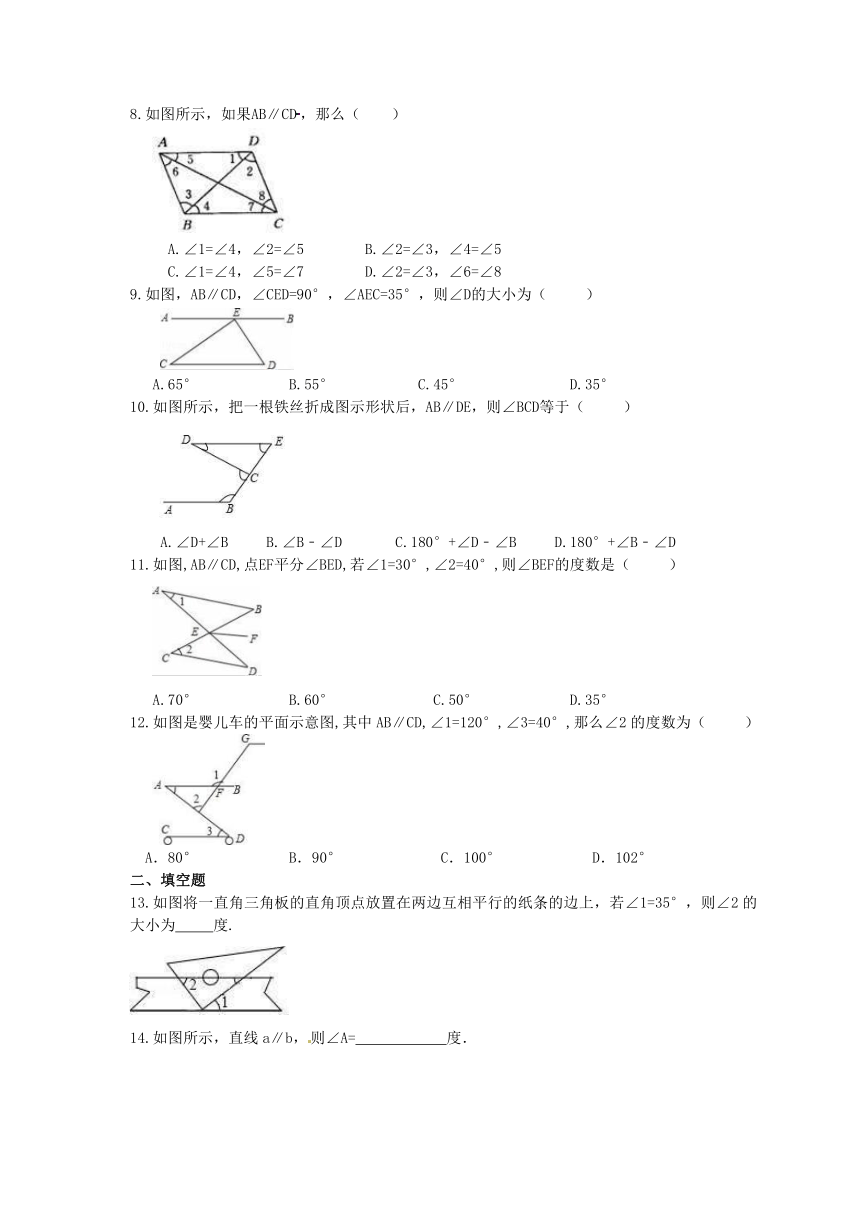
8.如图所示,如果AB∥CD,那么(
)
A.∠1=∠4,∠2=∠5
B.∠2=∠3,∠4=∠5
C.∠1=∠4,∠5=∠7
D.∠2=∠3,∠6=∠8
9.如图,AB∥CD,∠CED=90°,∠AEC=35°,则∠D的大小为(
)
A.65°
B.55°
C.45°
D.35°
10.如图所示,把一根铁丝折成图示形状后,AB∥DE,则∠BCD等于(
)
A.∠D+∠B
B.∠B﹣∠D
C.180°+∠D﹣∠B
D.180°+∠B﹣∠D
11.如图,AB∥CD,点EF平分∠BED,若∠1=30°,∠2=40°,则∠BEF的度数是(
)
A.70°
B.60°
C.50°
D.35°
12.如图是婴儿车的平面示意图,其中AB∥CD,∠1=120°,∠3=40°,那么∠2的度数为(
)
A.80°
B.90°
C.100°
D.102°
二、填空题
13.如图将一直角三角板的直角顶点放置在两边互相平行的纸条的边上,若∠1=35°,则∠2的大小为
度.
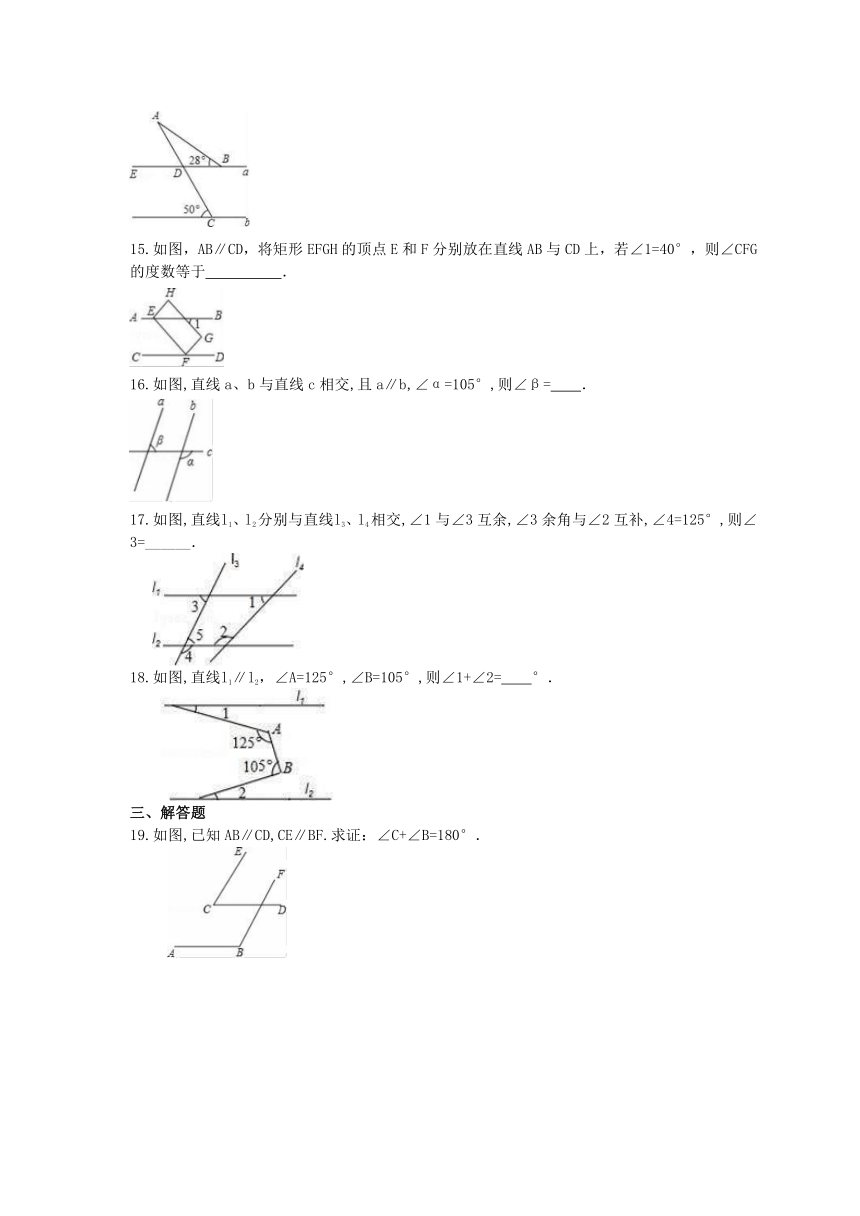
14.如图所示,直线a∥b,则∠A= 度.
15.如图,AB∥CD,将矩形EFGH的顶点E和F分别放在直线AB与CD上,若∠1=40°,则∠CFG的度数等于
.
16.如图,直线a、b与直线c相交,且a∥b,∠α=105°,则∠β=
.
17.如图,直线l1、l2分别与直线l3、l4相交,∠1与∠3互余,∠3余角与∠2互补,∠4=125°,则∠3=______.
18.如图,直线l1∥l2,∠A=125°,∠B=105°,则∠1+∠2=
°.
三、解答题
19.如图,已知AB∥CD,CE∥BF.求证:∠C+∠B=180°.
20.如图,已知D是BC上的一点,DE∥AC,DF∥AB.求证:∠A+∠B+∠C=180°.
21.如图,EP∥AB,PF∥CD,∠B=100°,∠C=120°,求∠EPF的度数.
22.如图,CD平分∠ACB,DE∥BC,∠AED=80°,求∠EDC的度数.
23.如图,已知AB∥CD,EF交AB于G,交CD于F,FH平分∠EFD,交AB于H
,∠AGE=500.求∠BHF的度数.
24.已知直线,直线与直线、分别相交于C、D两点.
(1)如图a,有一动点P在线段CD之间运动(不与C、D两点重合),问在点P的运动过程中,是否始终具有
∠3+∠1=∠2这一关系,为什么?
(2)如图b,当动点P线段CD之外运动(不与C、D两点重合),问上述结论是否成立?若不成立,试写出新的结论并说明理由.
参考答案
C
A
A
答案为:B.
D
D
B
答案为:D.
B
C
D
A
答案为:55.
答案为:22;
答案为:130°.
答案为:75°
答案为:55°.
答案为50.
证明:∵AB∥CD,CE∥BF,∴∠CDB+∠B=180°,
∠C=∠CDB,∴∠C+∠B=180°.
∵
DE∥AC(已知),
∴
∠BED=∠A,∠BDE=∠C(两直线平行,同位角相等).
∵
DF∥AB(已知),
∴
∠BED=∠EDF(两直线平行,内错角相等),
∠FDC=∠B(两直线平行,同位角相等).
∴
∠EDF=∠A(等量代换).
∵
∠BDE+∠EDF+∠FDC=180°(平角定义),
∴
∠C+∠A+∠B=180°(等量代换).
即
∠A+∠B+∠C=180°.
解:∵EP∥AB,
∴∠BPE=180°﹣∠B=180°﹣100°=80°,
∵PF∥CD,
∴∠CPF=180°﹣∠C=180°﹣120°=60°,
∴∠EPF=180°﹣∠BPE﹣∠CPF=180°﹣80°﹣60°=40°.
解:∵
DE∥BC,∠AED=80°,
∴
∠EDC=∠BCD,∠ACB=∠AED=80°.
∵
CD平分∠ACB,
∴
∠BCD=
0.5∠ACB=40°,
∴
∠EDC=∠BCD=40°.
略
解:(1)作PE∥,则∠1=∠APE
∵,
∴PE
∴∠3=∠BPE
∵∠APB=∠APE+∠BPE
∴∠APB=∠1+∠3
(2)上述结论不成立.
新结论:∠1=∠2+∠3
∵,
∴∠1=∠AFB
∵∠AFB=∠2+∠3
∴∠1=∠2+∠3
同步练习
一、选择题
1.如图,l1∥l2,∠1=56°,则∠2的度数为(
)
A.34°
B.56°
C.124°
D.146°
2.如图,一条公路两次转弯后又回到原来的方向,若第一次转弯时∠B=140°,则∠C的度数(
)
A.140°
B.40°
C.100°
D.180°
3.如图,直线m∥n,点A在直线m上,点B,C在直线n上,AB=BC,∠1=70°,CD⊥AB于D,那么∠2等于(
)
A.20°
B.30°
C.32°
D.25°
4.下面四个图形中,∠1=∠2一定成立的是(
)
5.如图,AB∥CD∥EF,BC∥AD,AC平分∠BAD,则图中与∠AGE相等的角(
)
A.2个
B.3个
C.4个
D.5个
6.如图,已知AB∥CD,BC平分∠ABE,∠C=33°,则∠CEF的度数是(
)
A.16°
B.33°
C.49°
D.66°
7.如图,已知a∥b,三角形直角顶点在直线a上,已知∠1=25°18/27//,则∠2度数是(
)
A.25°18/27//
B.640
41/33//
C.74°4133//
D.64°41/43//
8.如图所示,如果AB∥CD,那么(
)
A.∠1=∠4,∠2=∠5
B.∠2=∠3,∠4=∠5
C.∠1=∠4,∠5=∠7
D.∠2=∠3,∠6=∠8
9.如图,AB∥CD,∠CED=90°,∠AEC=35°,则∠D的大小为(
)
A.65°
B.55°
C.45°
D.35°
10.如图所示,把一根铁丝折成图示形状后,AB∥DE,则∠BCD等于(
)
A.∠D+∠B
B.∠B﹣∠D
C.180°+∠D﹣∠B
D.180°+∠B﹣∠D
11.如图,AB∥CD,点EF平分∠BED,若∠1=30°,∠2=40°,则∠BEF的度数是(
)
A.70°
B.60°
C.50°
D.35°
12.如图是婴儿车的平面示意图,其中AB∥CD,∠1=120°,∠3=40°,那么∠2的度数为(
)
A.80°
B.90°
C.100°
D.102°
二、填空题
13.如图将一直角三角板的直角顶点放置在两边互相平行的纸条的边上,若∠1=35°,则∠2的大小为
度.
14.如图所示,直线a∥b,则∠A= 度.
15.如图,AB∥CD,将矩形EFGH的顶点E和F分别放在直线AB与CD上,若∠1=40°,则∠CFG的度数等于
.
16.如图,直线a、b与直线c相交,且a∥b,∠α=105°,则∠β=
.
17.如图,直线l1、l2分别与直线l3、l4相交,∠1与∠3互余,∠3余角与∠2互补,∠4=125°,则∠3=______.
18.如图,直线l1∥l2,∠A=125°,∠B=105°,则∠1+∠2=
°.
三、解答题
19.如图,已知AB∥CD,CE∥BF.求证:∠C+∠B=180°.
20.如图,已知D是BC上的一点,DE∥AC,DF∥AB.求证:∠A+∠B+∠C=180°.
21.如图,EP∥AB,PF∥CD,∠B=100°,∠C=120°,求∠EPF的度数.
22.如图,CD平分∠ACB,DE∥BC,∠AED=80°,求∠EDC的度数.
23.如图,已知AB∥CD,EF交AB于G,交CD于F,FH平分∠EFD,交AB于H
,∠AGE=500.求∠BHF的度数.
24.已知直线,直线与直线、分别相交于C、D两点.
(1)如图a,有一动点P在线段CD之间运动(不与C、D两点重合),问在点P的运动过程中,是否始终具有
∠3+∠1=∠2这一关系,为什么?
(2)如图b,当动点P线段CD之外运动(不与C、D两点重合),问上述结论是否成立?若不成立,试写出新的结论并说明理由.
参考答案
C
A
A
答案为:B.
D
D
B
答案为:D.
B
C
D
A
答案为:55.
答案为:22;
答案为:130°.
答案为:75°
答案为:55°.
答案为50.
证明:∵AB∥CD,CE∥BF,∴∠CDB+∠B=180°,
∠C=∠CDB,∴∠C+∠B=180°.
∵
DE∥AC(已知),
∴
∠BED=∠A,∠BDE=∠C(两直线平行,同位角相等).
∵
DF∥AB(已知),
∴
∠BED=∠EDF(两直线平行,内错角相等),
∠FDC=∠B(两直线平行,同位角相等).
∴
∠EDF=∠A(等量代换).
∵
∠BDE+∠EDF+∠FDC=180°(平角定义),
∴
∠C+∠A+∠B=180°(等量代换).
即
∠A+∠B+∠C=180°.
解:∵EP∥AB,
∴∠BPE=180°﹣∠B=180°﹣100°=80°,
∵PF∥CD,
∴∠CPF=180°﹣∠C=180°﹣120°=60°,
∴∠EPF=180°﹣∠BPE﹣∠CPF=180°﹣80°﹣60°=40°.
解:∵
DE∥BC,∠AED=80°,
∴
∠EDC=∠BCD,∠ACB=∠AED=80°.
∵
CD平分∠ACB,
∴
∠BCD=
0.5∠ACB=40°,
∴
∠EDC=∠BCD=40°.
略
解:(1)作PE∥,则∠1=∠APE
∵,
∴PE
∴∠3=∠BPE
∵∠APB=∠APE+∠BPE
∴∠APB=∠1+∠3
(2)上述结论不成立.
新结论:∠1=∠2+∠3
∵,
∴∠1=∠AFB
∵∠AFB=∠2+∠3
∴∠1=∠2+∠3
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
