7.4.分式方程（2）

(共24张PPT)
7.4分式方程（2）
—— 分式方程的应用
某人上山和下山的路程都是s千米,上山的速度为a千米/小时,下山的速度为b千米/小时,则此人上山和下山的平均速度为( )
C
1.
如果分数 的分子分母同时加上同一个数后,分数的值变为它的倒数,那么加上的这个数是多少
解 :设这个数为x,则可列方程 ,
2.
某车间加工1200个零件，原来每天可加工x个，则
需________天可加工完成；如果采用新工艺，工效是
原来的1.5倍，这样每天可以加工_____个，同样多的
零件只要用 天可加工完成；如果比原来快了
10天完成，则可列方程：
1.5x
3.
例3：工厂生产一种电子配件，每只的成本为2元，毛利率为25%，后来该工厂通过改进工艺，降低了成本，在售价不变的情况下，毛利率增加了15%，问这种配件每只的成本降低了多少元？（精确到0.01元）
本题等量关系是什么？
毛利润＝售价－成本
设这种配件每只的成本降低了　元．
售出价是多少？
成本价是多少？
根据等量关系你能列出方程吗？
例3、工厂生产一种电子配件，每只的成本为2元，毛利率为25%，后来该工厂通过改进工艺，降低了成本，在售价不变的情况下，毛利率增加了15%，问这种配件每只的成本降低了多少元（精确到0.01元）？
解：设这种配件每只的成本降低了x元，改进工艺前，每只售价为,2（1+25%）=2.5（元）由题意，得
化简,得
解得,
经检验,x= 3/14是所列方程的根,且符合题意,.
答:每只的成本降低了0.21元
列分式方程解应用题的一般步骤
1.审:分析题意,找出数量关系和相等关系.
2.设:选择恰当的未知数,注意单位和语言完整.
3.列:根据数量和相等关系,正确列出代数式和方程.
4.解:求出所列方程的解.
5.验:有二次检验.
归纳小结
1
二次检验是:
(1)是不是所列方程的解;
(2)是否满足实际意义.
6.答:注意单位和语言完整.且答案要生活化.
甲、乙两人每小时共能做35个零件。甲、乙两人同时开始工作，当甲做了90个零件时，乙做了120个。问甲、乙每小时各做多少个零件？
课内练习 1
随堂练习
1
学以致用
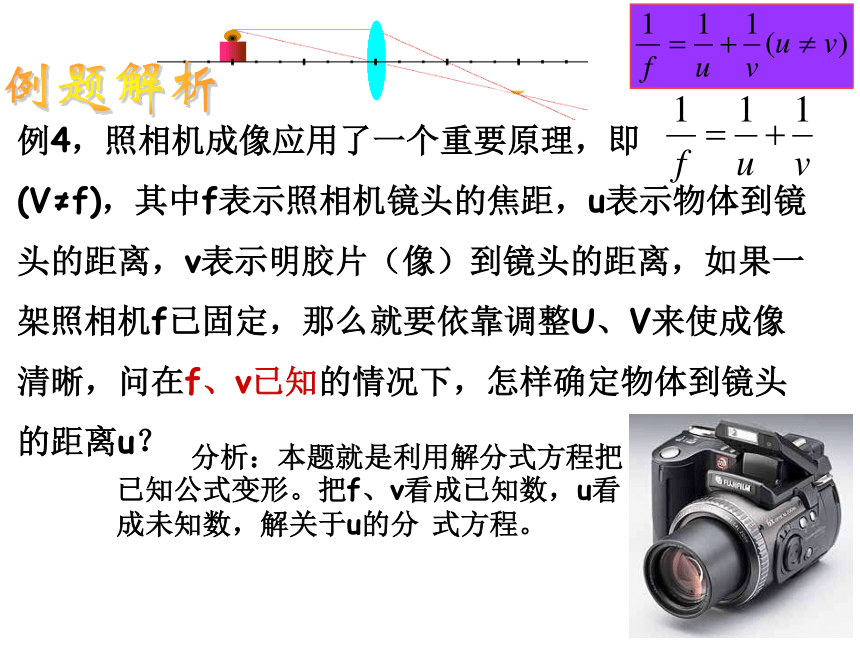
例4，照相机成像应用了一个重要原理，即 (V≠f)，其中f表示照相机镜头的焦距，u表示物体到镜头的距离，v表示明胶片（像）到镜头的距离，如果一架照相机f已固定，那么就要依靠调整U、V来使成像清晰，问在f、v已知的情况下，怎样确定物体到镜头的距离u？
分析：本题就是利用解分式方程把已知公式变形。把f、v看成已知数，u看成未知数，解关于u的分 式方程。
解 把f,v均看做已知数，解以u为未知数的方程：
移项，得
∴当f≠v时，
检验：因为v,f不为零，f≠v,所以 ，是分式方程 的根.
答：在已知f,v的情况下，物体到镜头的距离u可以由公式 来确定.
解题欣赏
公式变形：把要求表示的字母看成未知数，其它字母看成已知数，按解方程的思想来进行解答。
下面的公式变形对吗？如果不对，
应怎样改正？
随堂练习
3
课内练习 2
年新生婴儿数减去年死亡人数的差与年平均人口数的比叫做年人口的自然增长率，如果用p表示年新生婴儿数，q表示死亡人数，s表示年平均人口数，k表示年人口自然增长率，则年人口自然增长率k=
（1）把公式变形成已知k，p，q，求s的公式。
（2）把公式变形成已知k，s，p，求q的公式
合作交流，拓展延伸
在享受生活中感受数学
例5.某市从今年1月1日起调整居民用水价格,每m3水费上涨三分之一,小丽家去年12月的水费是15元,今年2月的水费是30元.已知今年2月的用水量比去年12月的用水量多5m3,求该市今年居民用水的价格
分析:此题的相等关系有：
小丽家今年2月份的用水量—小丽家去年12月份的用水量= 5m3.
每个月的用水量×水的单价=每个月的用水费.
今年的用水单价=去年用水单价×(1+1/3).
所以,首先要表示出小丽家这两个月的用水量.
每个月的用水量=水费/水的单价.
解:设该市去年用水的价格为x元/m3,则今年的水价为(1+1/3)x元/m3,根据题意得
解这个方程,得 x=1.5.
经检验,x=1.5是原方程的根.
1.5×4/3=2(元)
答:该市今年居民用水的价格为2元/m3.
例题欣赏
分式方程的应用:
列分式方程解应用题．
利用解分式方程把已知公式变形．
学以致用2
1.一艘轮船逆流航行2km的时间比顺流航行2 km的时间多用了40分钟, . (在横线上补充一个条件并提出一个问题)
如:已知水速为2 km/h,求船在静水中的速度
解:设船在静水中的速度为x km/h,根据题意得
你会解这个方程吗
方程两边都乘以3(x+2)(x-2),得
3(x+2)=3(x-2)+(x+2)(x-2).
x2=16.
解这个整式方程,得
x=±4
经检验,x= ±4都是原方程的根,但是x=-4不符合题意,应舍去.
答:船在静水中的速度是4km/h..
随堂练习
2
2.从甲地到乙地有两条公路：一条是全长600km的普通公路，另一条是全长480km的高速公路。某客车在高速公路上行驶的平均速度比在普通公路上快45km/h，由高速公路从甲地到乙地所需的时间是由普通公路从甲地到乙地所需时间的一半，求该客车由高速公路从甲地到乙地所需的时间。
这一问题中有哪些等量关系？
如果设客车由高速公路从甲地到乙地所需时间为x 小时，那么它由普通公路从甲地到乙地的时间为 h。根据题意可得方程：
480
600
=45
2x
x
某单位将沿街的一部分房屋出租,每间房屋的租金第二年比第一年多500元,所有房屋的租金第一年为9.6万元,第二年为10.2万元.
1.你能找出这一情境中的相等关系吗
2.根据这一情境你能提出哪些问题
扩展练习：
做一做
1
1. 这一情境中的等量关系有:
(1)第二年每间房屋的租金 =第一年每间房屋的租金 +500;
(2)第一年出租的房屋数=第二年出租的房屋数;
(3) 出租房屋的间数×每间房屋的租金=所有出租房屋的租金.
(4)……
2.根据这一情境可以提出的问题如:
(1).求出租房屋的总间数
(2).分别求两年每间出租房屋的租金
(3)……
做一做
2
3.你能解决这些问题吗
解1:设第一年每间房屋的租金为x元,则
解2:设共有x间出租房,则
你会解这两个方程吗
编写一道与下面分式方程相符的实际问题.
随堂练习
3
你,我,他——人人都有创造力. 相信自己是最棒的.