浙教版数学七年级下册第1章-平行线复习课件(共41张)
文档属性
| 名称 | 浙教版数学七年级下册第1章-平行线复习课件(共41张) |  | |
| 格式 | pptx | ||
| 文件大小 | 425.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-12 00:54:09 | ||
图片预览




文档简介
平行线复行线复习
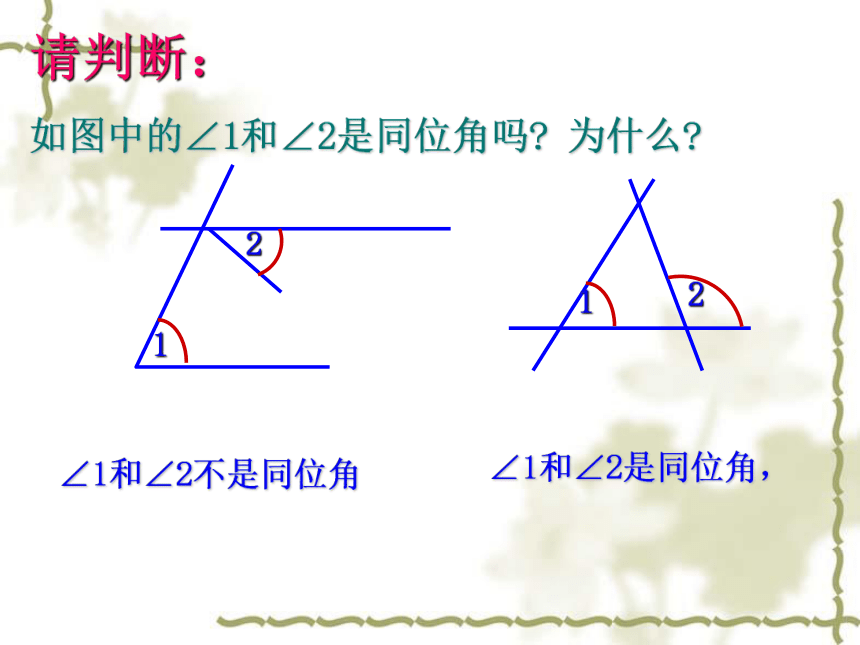
∠1和∠2不是同位角
请判断:
如图中的∠1和∠2是同位角吗?
为什么?
1
2
1
2
∠1和∠2是同位角,
1
2
3
4
5
6
7
8
a
b
c
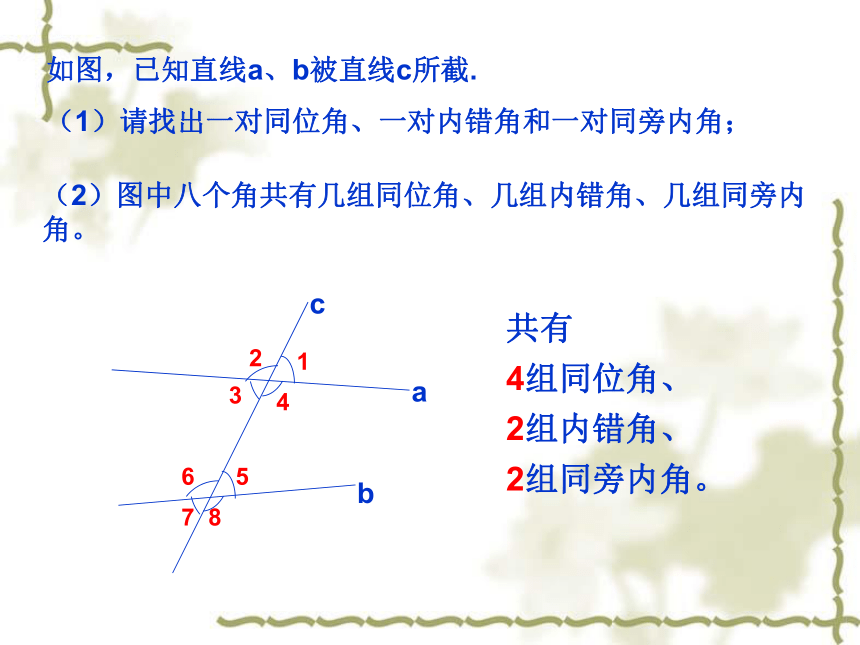
如图,已知直线a、b被直线c所截.
(1)请找出一对同位角、一对内错角和一对同旁内角;
(2)图中八个角共有几组同位角、几组内错角、几组同旁内角。
共有
4组同位角、
2组内错角、
2组同旁内角。
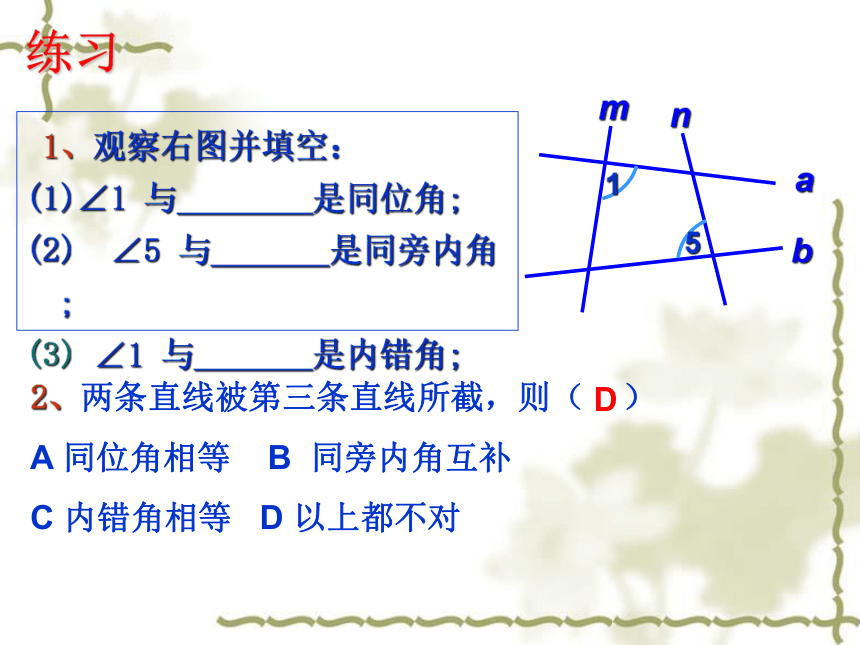
1、观察右图并填空:
∠1
与
是同位角;
∠5
与
是同旁内角;
(3)
∠1
与
是内错角;
b
a
n
m
1
5
2、两条直线被第三条直线所截,则(
)
A
同位角相等
B
同旁内角互补
C
内错角相等
D
以上都不对
D
练习
下列各题的解答有错吗?如果有,请分析错误的原因,并说出正确的解法.
1、若∠1和∠2是同位角,且∠2=
40°则
∠1的度数是(
)
A.50°
B.
40°
C.
140°
D.无法确定
一.热身训练
B
D
①.不相交的两条直线叫做平行线.( )
2
、判断下列说法是否正确
②.同旁内角有可能相等
.
( )
③.过一点有且只有一条直线与已知直线
平行 ( )
④.如果直线a
∥b,b∥c,那么a
∥c
( )
√
√
√
╳
╳
√
下列各题的解答有错吗?如果有,请分析错误的原因,并写出正确的解法.
一.热身训练
╳
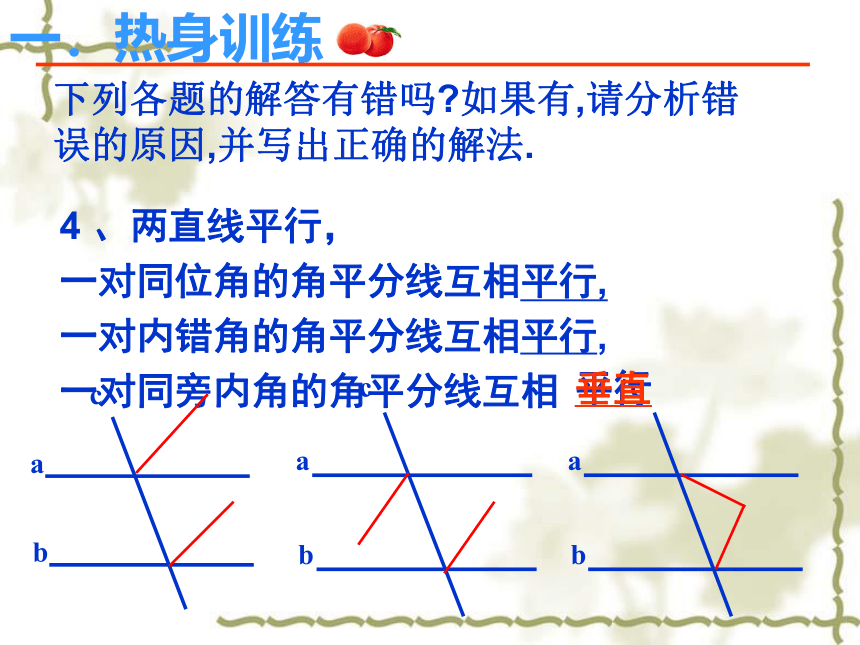
4
、两直线平行,
一对同位角的角平分线互相平行,
一对内错角的角平分线互相平行,
一对同旁内角的角平分线互相
a
b
c
a
b
c
a
b
c
平行
垂直
下列各题的解答有错吗?如果有,请分析错误的原因,并写出正确的解法.
一.热身训练
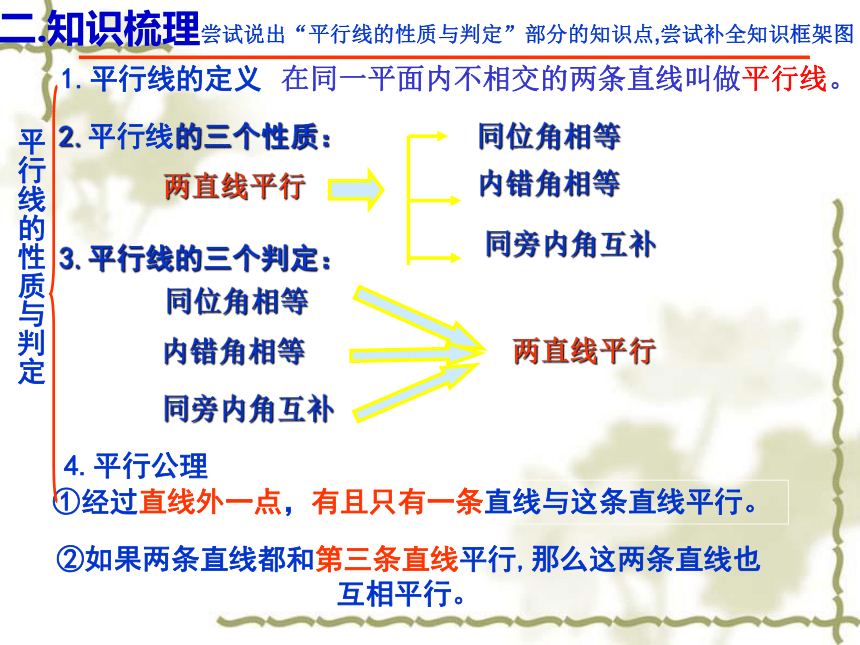
2.平行线的三个性质:
两直线平行
同位角相等
内错角相等
同旁内角互补
3.平行线的三个判定:
两直线平行
同位角相等
内错角相等
同旁内角互补
二.知识梳理尝试说出“平行线的性质与判定”部分的知识点,尝试补全知识框架图
1.平行线的定义
4.平行公理
②如果两条直线都和第三条直线平行,那么这两条直线也
互相平行。
①经过直线外一点,有且只有一条直线与这条直线平行。
在同一平面内不相交的两条直线叫做平行线。
平行线的性质与判定
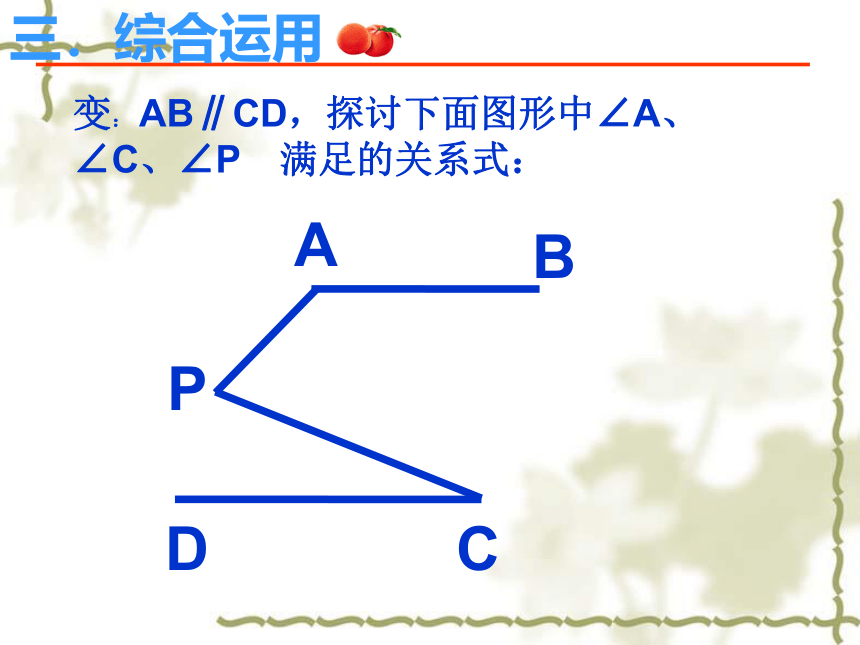
变:
AB∥CD,探讨下面图形中∠A、∠C、∠P 满足的关系式:
B
C
P
A
D
三.综合运用
四
.探究规律,提炼方法,总结提高
从知识点或题型上给上述例题归类,并谈谈解题经验或思想方法
例1
主要涉及到平行线的判定和性质等知识点.答案开放,需要多角度考虑
例2
利用平行线进行角的转化,方法多种。
例3
体现了分类讨论思想和方程思想
例4
图形多变,方法灵活,但都可以通过添平行线或构造三角形解决,把复杂的图形转化为基本图形是解题的关键
五
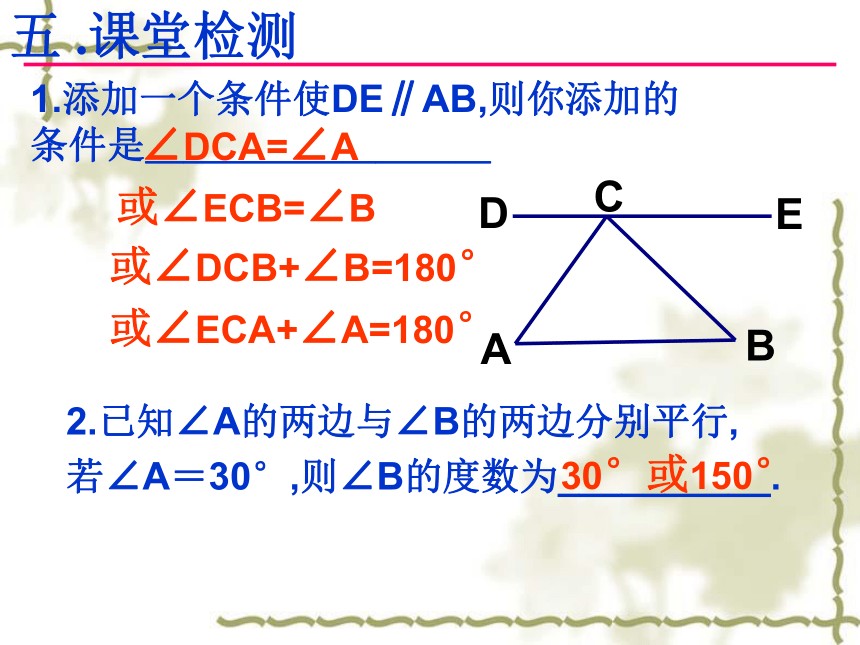
.课堂检测
1.添加一个条件使DE∥AB,则你添加的条件是_________
2.已知∠A的两边与∠B的两边分别平行,
若∠A=30°,则∠B的度数为__________.
D
E
A
B
C
∠DCA=∠A
或∠ECB=∠B
或∠DCB+∠B=180°
或∠ECA+∠A=180°
30°或150°
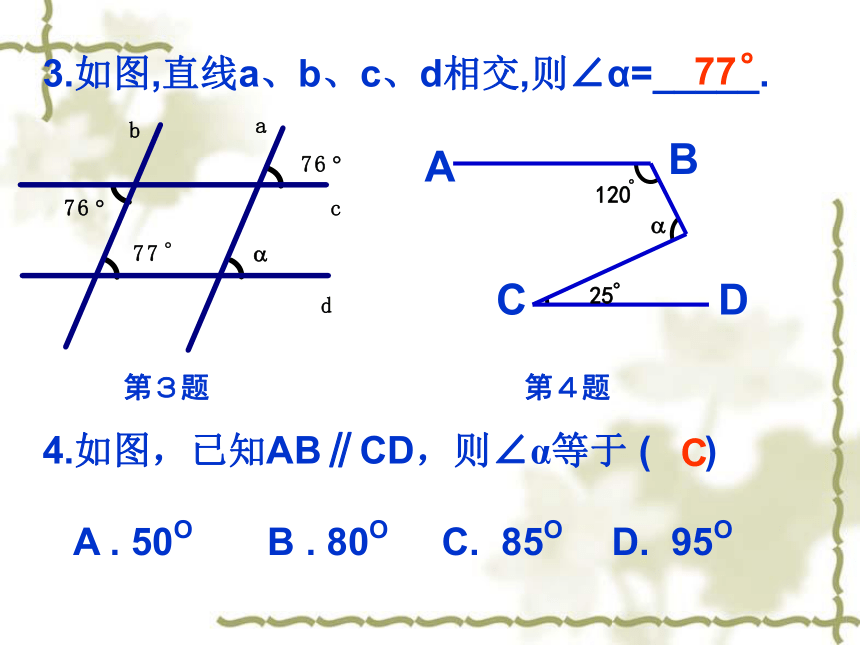
3.如图,直线a、b、c、d相交,则∠α=_____.
第3题
4.如图,已知AB∥CD,则∠α等于
(
)
A
.
50O
B
.
80O
C.
85O
D.
95O
D
C
A
B
第4题
a
25
°
120
°
77°
C
作业:
讲义一张
5.如图,已知FC∥AB∥DE,∠3:∠D:∠B=2:3:4,
求∠3,∠D,∠B的度数。
3
2
1
F
E
D
C
B
A
提高题
三
.综合运用知识
2、如图,已知
FC∥AB∥DE,
∠3:∠D:∠B=2:3:4,
求∠3,∠D,∠B的度数。
3
2
1
F
E
D
C
B
A
3如图,直线AB,CD,EF被直线GH所截,∠1=70°,∠2=110°,∠2+∠3=180°.请判定直线EF与AB平行吗?为什么?
A
B
C
D
E
F
G
H
1
2
3
4
1、如图所示,∠1=72°,∠2=72°,∠3=60°,求∠4的度数
。
3、如图,
(1)若∠2=∠3,则a∥b,理由是 ;
(2)若a∥b,则∠3=∠4,
理由是 。
3.如图,直线a、b、c、d相交,则∠α=___.
4.如图,一个宽度相等的纸条,如图折叠一下,那么∠1= 。
110O
1
添加辅助线的方法:
①添加平行线
②构造三角形
连结线段
作延长线
例1.如图,∠1=∠2,能判断AB∥DF吗?为什么?
?
?
?
?
?
?
F
D
C
A
B
E
1
2
添加∠CBD=∠EDB
内错角相等,两直线平行
想想还可以添加什么条件?
(请先想一想,再讲给同学听)
三.综合运用知识
不能
若不能判断AB∥DF,你认为还需要再添加的一个条件是什么呢?写出这个条件,并说明你的理由。
直线所截被第三条
课堂小结
1.知识性小结:
平行线的性质
应用
求角
两条平行线
同位角相等
内错角相等
同旁内角互补
例2:已知:如图:
BD平分
ABC,
1=
2
,
C=70?,
求
ADE
的度数。
3
2
1
A
E
D
C
B
课堂小结
2.思想方法小结:
添加辅助线的方法
添加平行线
构造三角形
构造基本图形
化归的数学思想
(同旁内角 ,两直线平行)
下列各题的解答有错吗?如果有,请分析错误的原因,并写出正确的解法.
(同位角相等,两直线平行)
∠3
∠5
相等
互补
①
∵
∠1
=
(已知)
④
∵
∠1
=
∠4
(已知)
∴
CE∥AB
②
∵
(已知)
∠2
③
∵
∠4
+_____=180o(已知)
∴
CD∥BF
如图:填空
1
3
5
4
2
C
F
E
A
D
B
(两直线平行,内错角相等)
(同旁内角互补,两直线平行)
∴
CD∥BF
∴
CE∥AB
∴
CE∥AB
∠3=∠4
∠3+∠4=180°
∠1和∠4不是同位角,也不是内错角,
不能判断两直线平行
一.热身训练
(内错角相等,两直线平行)
平行线的性质:
练习:如果∠A和∠B是同位角,∠A=60。,则∠B的度数
(
)
A.60。
B.
120。
C.
60。或
120。
D.不能确定
D
注意:同位角不一定相等。同位角相等是平行线特有的性质,只有当两直线平行时,才有同位角相等。
如图,在△ABC中,CD⊥AB于D,
FG⊥AB于G,ED//BC,试说明
∠1=∠2的理由。
.
F
E
D
A
B
C
G
1
2
三.综合运用
如图,AB∥CD,直线FE与两平行线交于点G、H,形成的同位角的角平分线的位置上有什么关系?
A
B
C
D
E
F
G
H
M
N
探究思考:
变式一:如图,AB∥CD,直线FE与两平行线交于点G、H,形成的内错角的角平分线的位置上又有什么关系?
A
B
C
D
E
F
G
H
M
N
思维拓展
?
变式二:如图,AB∥CD,直线FE与两平行线交于点G、H,形成的同旁内角的角平分线的位置上又有什么关系?
A
B
C
D
E
F
G
H
M
思维拓展
?
7、如图,已知AB∥CD,试问:∠B、∠BED、∠D有什么关系?并说明理由。
A
B
C
D
E
F
变式.如图,已知AB∥CD
,
∠B、∠BED、∠D有什么关系?并说明理由。
A
B
C
D
E
F
问题2:如图,已知:AB∥CD
求证:
∠C=∠A+∠P
A
D
P
C
B
M
N
1.如图AB∥CD
求
∠A+
∠E
+∠F
+∠C的度数
B
A
E
F
C
D
拓
展
①已知:AB∥CD,
∠B=110°,∠C=18°,
则∠BPC=________
②已知:AB∥CD,
∠1=140°,∠2=60°,
则∠3=________
③已知:AB∥EF,
∠B=30°,
∠F=40°,∠D=100°,
则∠C=________
A
B
C
D
P
A
B
C
D
F
E
提高题
E
A
B
C
D
1
2
3
如图,将一条两边沿互相平行的纸带按如图折叠.设∠1=50度,请用关于x的代数式表示∠2的度数.
1
2
2
1
变一变:将一条两边沿互相平行的纸带按如图折叠,∠1=30度,请求出∠2的度数。
如果一个角的两边与另一个角的两边分别平行,那么这两个角有什么关系?
已知:
AB∥DE
BC∥EF
小结:一个角的两边与另一个角的两边分别平行,则这两个角相等或互补。
∠B=∠E
∠B
+
∠E
=180o
探究
(1)
1
G
F
E
D
C
B
A
(2)
1
G
F
E
D
C
B
A
例3.已知∠A的两边与∠B的两边分别平行,若∠A的度数比∠B的2倍少30°,求∠B的度数?
请运用上面的结论解决下列问题
三.综合运用
A1
A2
A1
A3
A2
图1
图2
M
M
M
N
N
A3
A1
A4
图3
N
A3
A1
A2
A4
A5
图4
M
N
A3
A4
A5
A6
An
图5
M
N
7.如图1,MA1∥NA2,则∠A1+∠A2=_________________度.
如图2,MA1∥NA3,则∠A1+∠A2+∠A3=_____________
度.
如图3,MA1∥NA4,则∠A1+∠A2+∠A3+∠A4=________度.
如图4,MA1∥NA5,则∠A1+∠A2+∠A3+∠A4+∠A5=__度.
从上述结论中你发现了什么规律?
A2
A1
A2
如图5,MA1∥NAn,则∠A1+∠A2+∠A3+……+∠An=_________________度.
如图:一条公路两次转弯后,和原来的方向相同,如果第一次拐的角是138°,即∠ABC.
问题1:你能知道第二次拐的角
∠BCD是多少吗?
问题2:你是怎么想的?
问题3:在解决这个问题中
,用到了哪些知识
?
A
B
C
D
添加辅助线的方法:
①添加平行线
②构造三角形
连结线段
作延长线
4.如图,一个宽度相等的纸条,如图折叠一下,那么∠1= 。
110O
1
∠1和∠2不是同位角
请判断:
如图中的∠1和∠2是同位角吗?
为什么?
1
2
1
2
∠1和∠2是同位角,
1
2
3
4
5
6
7
8
a
b
c
如图,已知直线a、b被直线c所截.
(1)请找出一对同位角、一对内错角和一对同旁内角;
(2)图中八个角共有几组同位角、几组内错角、几组同旁内角。
共有
4组同位角、
2组内错角、
2组同旁内角。
1、观察右图并填空:
∠1
与
是同位角;
∠5
与
是同旁内角;
(3)
∠1
与
是内错角;
b
a
n
m
1
5
2、两条直线被第三条直线所截,则(
)
A
同位角相等
B
同旁内角互补
C
内错角相等
D
以上都不对
D
练习
下列各题的解答有错吗?如果有,请分析错误的原因,并说出正确的解法.
1、若∠1和∠2是同位角,且∠2=
40°则
∠1的度数是(
)
A.50°
B.
40°
C.
140°
D.无法确定
一.热身训练
B
D
①.不相交的两条直线叫做平行线.( )
2
、判断下列说法是否正确
②.同旁内角有可能相等
.
( )
③.过一点有且只有一条直线与已知直线
平行 ( )
④.如果直线a
∥b,b∥c,那么a
∥c
( )
√
√
√
╳
╳
√
下列各题的解答有错吗?如果有,请分析错误的原因,并写出正确的解法.
一.热身训练
╳
4
、两直线平行,
一对同位角的角平分线互相平行,
一对内错角的角平分线互相平行,
一对同旁内角的角平分线互相
a
b
c
a
b
c
a
b
c
平行
垂直
下列各题的解答有错吗?如果有,请分析错误的原因,并写出正确的解法.
一.热身训练
2.平行线的三个性质:
两直线平行
同位角相等
内错角相等
同旁内角互补
3.平行线的三个判定:
两直线平行
同位角相等
内错角相等
同旁内角互补
二.知识梳理尝试说出“平行线的性质与判定”部分的知识点,尝试补全知识框架图
1.平行线的定义
4.平行公理
②如果两条直线都和第三条直线平行,那么这两条直线也
互相平行。
①经过直线外一点,有且只有一条直线与这条直线平行。
在同一平面内不相交的两条直线叫做平行线。
平行线的性质与判定
变:
AB∥CD,探讨下面图形中∠A、∠C、∠P 满足的关系式:
B
C
P
A
D
三.综合运用
四
.探究规律,提炼方法,总结提高
从知识点或题型上给上述例题归类,并谈谈解题经验或思想方法
例1
主要涉及到平行线的判定和性质等知识点.答案开放,需要多角度考虑
例2
利用平行线进行角的转化,方法多种。
例3
体现了分类讨论思想和方程思想
例4
图形多变,方法灵活,但都可以通过添平行线或构造三角形解决,把复杂的图形转化为基本图形是解题的关键
五
.课堂检测
1.添加一个条件使DE∥AB,则你添加的条件是_________
2.已知∠A的两边与∠B的两边分别平行,
若∠A=30°,则∠B的度数为__________.
D
E
A
B
C
∠DCA=∠A
或∠ECB=∠B
或∠DCB+∠B=180°
或∠ECA+∠A=180°
30°或150°
3.如图,直线a、b、c、d相交,则∠α=_____.
第3题
4.如图,已知AB∥CD,则∠α等于
(
)
A
.
50O
B
.
80O
C.
85O
D.
95O
D
C
A
B
第4题
a
25
°
120
°
77°
C
作业:
讲义一张
5.如图,已知FC∥AB∥DE,∠3:∠D:∠B=2:3:4,
求∠3,∠D,∠B的度数。
3
2
1
F
E
D
C
B
A
提高题
三
.综合运用知识
2、如图,已知
FC∥AB∥DE,
∠3:∠D:∠B=2:3:4,
求∠3,∠D,∠B的度数。
3
2
1
F
E
D
C
B
A
3如图,直线AB,CD,EF被直线GH所截,∠1=70°,∠2=110°,∠2+∠3=180°.请判定直线EF与AB平行吗?为什么?
A
B
C
D
E
F
G
H
1
2
3
4
1、如图所示,∠1=72°,∠2=72°,∠3=60°,求∠4的度数
。
3、如图,
(1)若∠2=∠3,则a∥b,理由是 ;
(2)若a∥b,则∠3=∠4,
理由是 。
3.如图,直线a、b、c、d相交,则∠α=___.
4.如图,一个宽度相等的纸条,如图折叠一下,那么∠1= 。
110O
1
添加辅助线的方法:
①添加平行线
②构造三角形
连结线段
作延长线
例1.如图,∠1=∠2,能判断AB∥DF吗?为什么?
?
?
?
?
?
?
F
D
C
A
B
E
1
2
添加∠CBD=∠EDB
内错角相等,两直线平行
想想还可以添加什么条件?
(请先想一想,再讲给同学听)
三.综合运用知识
不能
若不能判断AB∥DF,你认为还需要再添加的一个条件是什么呢?写出这个条件,并说明你的理由。
直线所截被第三条
课堂小结
1.知识性小结:
平行线的性质
应用
求角
两条平行线
同位角相等
内错角相等
同旁内角互补
例2:已知:如图:
BD平分
ABC,
1=
2
,
C=70?,
求
ADE
的度数。
3
2
1
A
E
D
C
B
课堂小结
2.思想方法小结:
添加辅助线的方法
添加平行线
构造三角形
构造基本图形
化归的数学思想
(同旁内角 ,两直线平行)
下列各题的解答有错吗?如果有,请分析错误的原因,并写出正确的解法.
(同位角相等,两直线平行)
∠3
∠5
相等
互补
①
∵
∠1
=
(已知)
④
∵
∠1
=
∠4
(已知)
∴
CE∥AB
②
∵
(已知)
∠2
③
∵
∠4
+_____=180o(已知)
∴
CD∥BF
如图:填空
1
3
5
4
2
C
F
E
A
D
B
(两直线平行,内错角相等)
(同旁内角互补,两直线平行)
∴
CD∥BF
∴
CE∥AB
∴
CE∥AB
∠3=∠4
∠3+∠4=180°
∠1和∠4不是同位角,也不是内错角,
不能判断两直线平行
一.热身训练
(内错角相等,两直线平行)
平行线的性质:
练习:如果∠A和∠B是同位角,∠A=60。,则∠B的度数
(
)
A.60。
B.
120。
C.
60。或
120。
D.不能确定
D
注意:同位角不一定相等。同位角相等是平行线特有的性质,只有当两直线平行时,才有同位角相等。
如图,在△ABC中,CD⊥AB于D,
FG⊥AB于G,ED//BC,试说明
∠1=∠2的理由。
.
F
E
D
A
B
C
G
1
2
三.综合运用
如图,AB∥CD,直线FE与两平行线交于点G、H,形成的同位角的角平分线的位置上有什么关系?
A
B
C
D
E
F
G
H
M
N
探究思考:
变式一:如图,AB∥CD,直线FE与两平行线交于点G、H,形成的内错角的角平分线的位置上又有什么关系?
A
B
C
D
E
F
G
H
M
N
思维拓展
?
变式二:如图,AB∥CD,直线FE与两平行线交于点G、H,形成的同旁内角的角平分线的位置上又有什么关系?
A
B
C
D
E
F
G
H
M
思维拓展
?
7、如图,已知AB∥CD,试问:∠B、∠BED、∠D有什么关系?并说明理由。
A
B
C
D
E
F
变式.如图,已知AB∥CD
,
∠B、∠BED、∠D有什么关系?并说明理由。
A
B
C
D
E
F
问题2:如图,已知:AB∥CD
求证:
∠C=∠A+∠P
A
D
P
C
B
M
N
1.如图AB∥CD
求
∠A+
∠E
+∠F
+∠C的度数
B
A
E
F
C
D
拓
展
①已知:AB∥CD,
∠B=110°,∠C=18°,
则∠BPC=________
②已知:AB∥CD,
∠1=140°,∠2=60°,
则∠3=________
③已知:AB∥EF,
∠B=30°,
∠F=40°,∠D=100°,
则∠C=________
A
B
C
D
P
A
B
C
D
F
E
提高题
E
A
B
C
D
1
2
3
如图,将一条两边沿互相平行的纸带按如图折叠.设∠1=50度,请用关于x的代数式表示∠2的度数.
1
2
2
1
变一变:将一条两边沿互相平行的纸带按如图折叠,∠1=30度,请求出∠2的度数。
如果一个角的两边与另一个角的两边分别平行,那么这两个角有什么关系?
已知:
AB∥DE
BC∥EF
小结:一个角的两边与另一个角的两边分别平行,则这两个角相等或互补。
∠B=∠E
∠B
+
∠E
=180o
探究
(1)
1
G
F
E
D
C
B
A
(2)
1
G
F
E
D
C
B
A
例3.已知∠A的两边与∠B的两边分别平行,若∠A的度数比∠B的2倍少30°,求∠B的度数?
请运用上面的结论解决下列问题
三.综合运用
A1
A2
A1
A3
A2
图1
图2
M
M
M
N
N
A3
A1
A4
图3
N
A3
A1
A2
A4
A5
图4
M
N
A3
A4
A5
A6
An
图5
M
N
7.如图1,MA1∥NA2,则∠A1+∠A2=_________________度.
如图2,MA1∥NA3,则∠A1+∠A2+∠A3=_____________
度.
如图3,MA1∥NA4,则∠A1+∠A2+∠A3+∠A4=________度.
如图4,MA1∥NA5,则∠A1+∠A2+∠A3+∠A4+∠A5=__度.
从上述结论中你发现了什么规律?
A2
A1
A2
如图5,MA1∥NAn,则∠A1+∠A2+∠A3+……+∠An=_________________度.
如图:一条公路两次转弯后,和原来的方向相同,如果第一次拐的角是138°,即∠ABC.
问题1:你能知道第二次拐的角
∠BCD是多少吗?
问题2:你是怎么想的?
问题3:在解决这个问题中
,用到了哪些知识
?
A
B
C
D
添加辅助线的方法:
①添加平行线
②构造三角形
连结线段
作延长线
4.如图,一个宽度相等的纸条,如图折叠一下,那么∠1= 。
110O
1
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
