浙教版数学七年级下册3.1同底数幂的乘法课件(12张)
文档属性
| 名称 | 浙教版数学七年级下册3.1同底数幂的乘法课件(12张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 00:00:00 | ||
图片预览




文档简介
(共12张PPT)
3.1同底数幂的乘法(1)
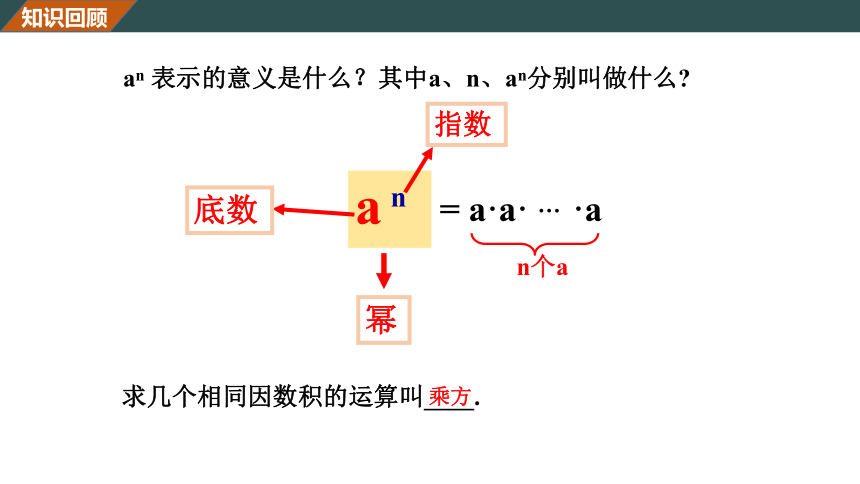
知识回顾
an
表示的意义是什么?其中a、n、an分别叫做什么?
a
n
指数
幂
n个a
底数
=
a·a·
…
·a
求几个相同因数积的运算叫____.
乘方
知识回顾
填
空
(1)2
表示________________;
5
2×2×2×2×2
(2)10×10×10×10可以写成____;
10
4
(3)
a的底数是__,指数是__;
a
1
(4)(a+b)
的底数是______,指数是_____;
3
a+b
3
(5)(-2)
的底数是___,指数是__;
4
-2
4
(6)
-2
的底数是___,指数是__.
4
2
4
思考:式子1015×103中的两个
因数有何特点?
底数相同
我们把底数相同的幂称为同底数幂
导入新课
5
(2×2×2)×(2×2)
5
(a
a
a)
(a
a)
5
=
a
a
a
a
a
(10×10×10)×(10×10)
=
10(
)
=
2(
)
;
请同学们先根据自己的理解,解答下列各题.
103
×102
=
23
×22
=
=2×2×2×2×2
a3×a2
=
=
a(
)
.
猜想:
am
·
an=
?
(当m、n都是正整数)
分组讨论,并尝试证明你的猜想是否正确.
导入新课
猜想:
am
·
an=
(m、n都是正整数)
am+n
am
·
an
=
(aa…a)
m个a
·
(aa…a)
n个a
(乘方的意义)
=
aa…a
(m+n)个a
(乘法结合律)
=am+n
(乘方的意义)
由此可得同底数幂的乘法性质:
am
·
an
=
am+n
(m、n都是正整数)
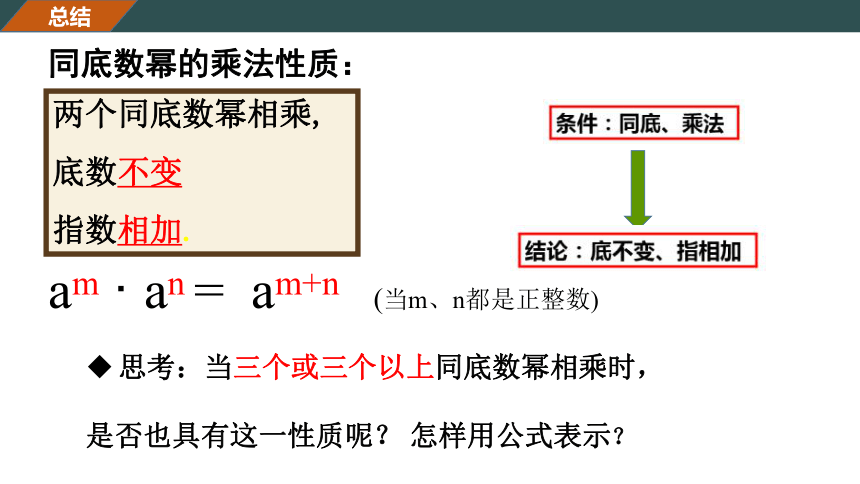
总结
同底数幂的乘法性质:
am
·
an
=
am+n
(当m、n都是正整数)
两个同底数幂相乘,
底数不变
指数相加.
思考:当三个或三个以上同底数幂相乘时,
是否也具有这一性质呢?
怎样用公式表示?
典例分析
例1:计算下列各式,结果用幂的形式表示.
解:
做一做
运用同底数幂的乘法法则计算下列各式,并用幂的形式表示结果.
(1)
3×39
(2)
106×106
(3)
(-3)2×(-3
)9
(4)
(5)
-24×23×25
(6)
新课讲解
例2:
我国“天河一1A”超级计算机的实测运算速度达到每秒2.
566千万亿次.如果按这个速度工作一整天,那么它能运算多少次?
解:
2.
566千万亿次=2
.
566
×107
×
108次,24小时=24
×3.6×103秒.由乘法的交换律和结合律,得:
(
2.
566
×
107×108)
×
(24
×3.6
×
103)
=(2.566×24×3.6)×(107×
108×103)
=221.702
4
×
1018≈2.2
×
1020(次).
答:它一天约能运算2.2
×
1020次.
应用提高
1.已知x3?xa?x2a+1=x31,求a的值.
解:x3?xa?x2a+1=x3+a+2a+1=a3a+4,
3a+4=31,
a=9.
2.已知2x=3,2y=6,2z=36,试写出x,y,z的关系式.
解:∵2x=3,2y=6,2z=36,
∴2×2x×2y=2z,
即
21+x+y=2z,
故
1+x+y=z.
课堂小结
同底数幂相乘.底数不变.指数相加.
(m,n都是正整数)
课后作业
1.课前课后3.1(1)
2.走进重高相关题目
3.1同底数幂的乘法(1)
知识回顾
an
表示的意义是什么?其中a、n、an分别叫做什么?
a
n
指数
幂
n个a
底数
=
a·a·
…
·a
求几个相同因数积的运算叫____.
乘方
知识回顾
填
空
(1)2
表示________________;
5
2×2×2×2×2
(2)10×10×10×10可以写成____;
10
4
(3)
a的底数是__,指数是__;
a
1
(4)(a+b)
的底数是______,指数是_____;
3
a+b
3
(5)(-2)
的底数是___,指数是__;
4
-2
4
(6)
-2
的底数是___,指数是__.
4
2
4
思考:式子1015×103中的两个
因数有何特点?
底数相同
我们把底数相同的幂称为同底数幂
导入新课
5
(2×2×2)×(2×2)
5
(a
a
a)
(a
a)
5
=
a
a
a
a
a
(10×10×10)×(10×10)
=
10(
)
=
2(
)
;
请同学们先根据自己的理解,解答下列各题.
103
×102
=
23
×22
=
=2×2×2×2×2
a3×a2
=
=
a(
)
.
猜想:
am
·
an=
?
(当m、n都是正整数)
分组讨论,并尝试证明你的猜想是否正确.
导入新课
猜想:
am
·
an=
(m、n都是正整数)
am+n
am
·
an
=
(aa…a)
m个a
·
(aa…a)
n个a
(乘方的意义)
=
aa…a
(m+n)个a
(乘法结合律)
=am+n
(乘方的意义)
由此可得同底数幂的乘法性质:
am
·
an
=
am+n
(m、n都是正整数)
总结
同底数幂的乘法性质:
am
·
an
=
am+n
(当m、n都是正整数)
两个同底数幂相乘,
底数不变
指数相加.
思考:当三个或三个以上同底数幂相乘时,
是否也具有这一性质呢?
怎样用公式表示?
典例分析
例1:计算下列各式,结果用幂的形式表示.
解:
做一做
运用同底数幂的乘法法则计算下列各式,并用幂的形式表示结果.
(1)
3×39
(2)
106×106
(3)
(-3)2×(-3
)9
(4)
(5)
-24×23×25
(6)
新课讲解
例2:
我国“天河一1A”超级计算机的实测运算速度达到每秒2.
566千万亿次.如果按这个速度工作一整天,那么它能运算多少次?
解:
2.
566千万亿次=2
.
566
×107
×
108次,24小时=24
×3.6×103秒.由乘法的交换律和结合律,得:
(
2.
566
×
107×108)
×
(24
×3.6
×
103)
=(2.566×24×3.6)×(107×
108×103)
=221.702
4
×
1018≈2.2
×
1020(次).
答:它一天约能运算2.2
×
1020次.
应用提高
1.已知x3?xa?x2a+1=x31,求a的值.
解:x3?xa?x2a+1=x3+a+2a+1=a3a+4,
3a+4=31,
a=9.
2.已知2x=3,2y=6,2z=36,试写出x,y,z的关系式.
解:∵2x=3,2y=6,2z=36,
∴2×2x×2y=2z,
即
21+x+y=2z,
故
1+x+y=z.
课堂小结
同底数幂相乘.底数不变.指数相加.
(m,n都是正整数)
课后作业
1.课前课后3.1(1)
2.走进重高相关题目
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
