1.4.1 平行线的性质同步练习(含解析)
文档属性
| 名称 | 1.4.1 平行线的性质同步练习(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 319.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 00:00:00 | ||
图片预览


文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
初中数学浙教版七年级下册1.4
平行线的性质(1)
同步练习
一、单选题(共5题;共10分)
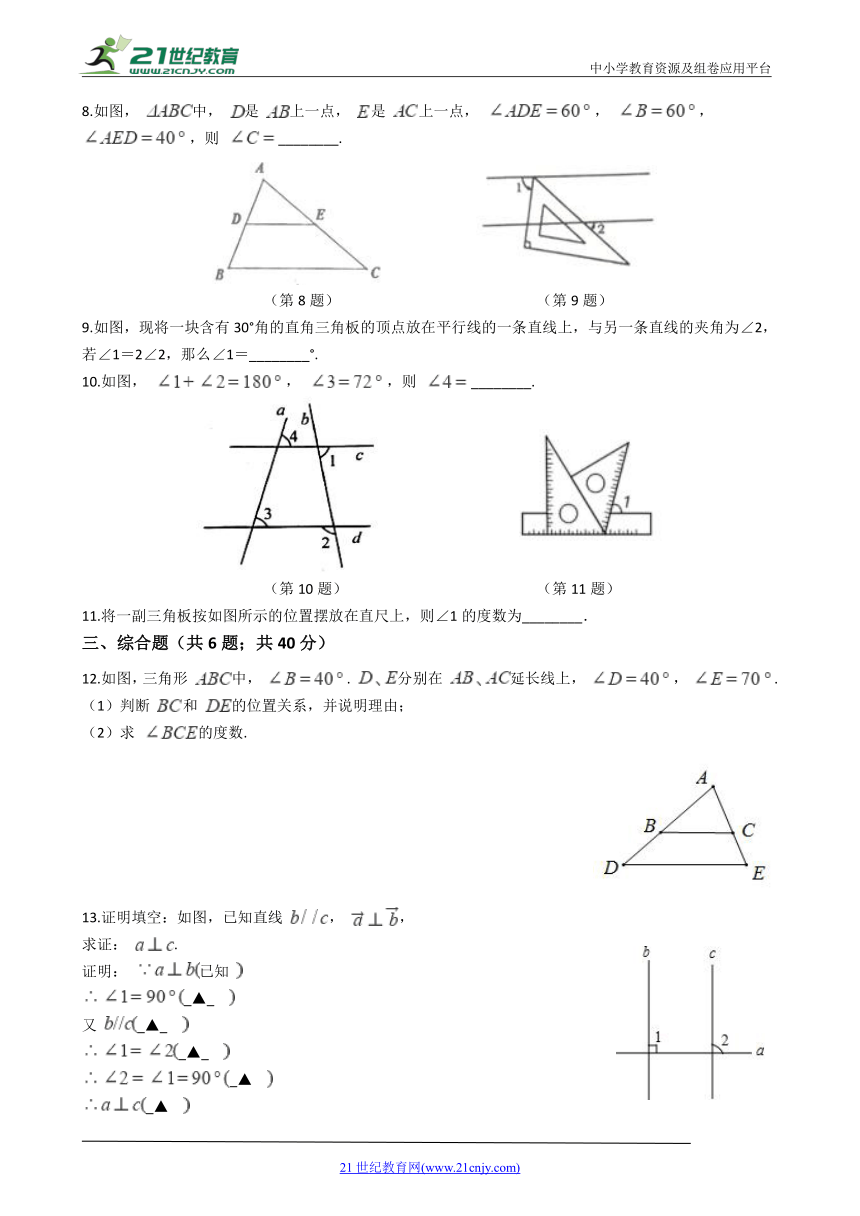
1.如图,已知直线
,
,则
的度数为(???
)
????????????????????????????????????B.????????????????????????????????????C.????????????????????????????????????D.?
(第1题)
(第2题)
2.如图,直线
与直线
相交,已知
,则
的度数是(?
)
A.???????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
3.如图,三角板的直角顶点落在矩形纸片的一边上.若
,则
的度数是(??
)
?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
(第3题)
(第4题)
4.如图.直线a∥b,直线L与a、b分别交于点A,B,过点A作AC⊥b于点C.若∠1=50°,则∠2的度数为(?
)
A.?130°??????????????????????????????????????B.?50°??????????????????????????????????????C.?40°??????????????????????????????????????D.?25°
5.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的角度是(?
)
A.?第一次右拐60°,第二次左拐120°
B.?第一次左拐60°,第二次右拐60°
C.?第一次左拐60°,第二次左拐120°
D.?第一次右拐60°,第二次右拐60°
二、填空题(共6题;共6分)
6.如图所示,直线a∥b,如果∠1=45°,那么∠2的度数是________.
(第6题)
(第7题)
7.已知:如图,直线a∥b
,
直线c与a
,
b相交,若∠2=115°,则∠1=________度.
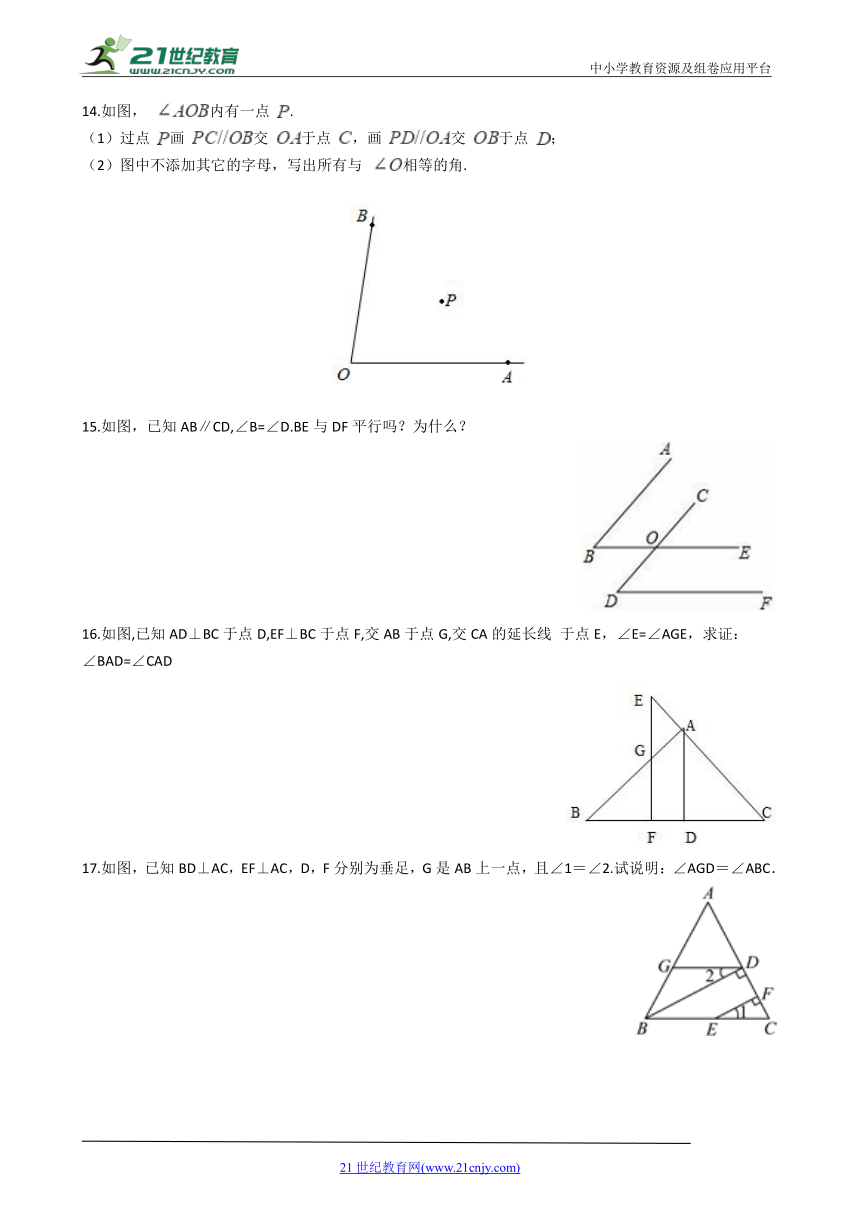
8.如图,
中,
是
上一点,
是
上一点,
,
,
,则
________.
(第8题)
(第9题)
9.如图,现将一块含有30°角的直角三角板的顶点放在平行线的一条直线上,与另一条直线的夹角为∠2,若∠1=2∠2,那么∠1=________°.
10.如图,
,
,则
________.
(第10题)
(第11题)
11.将一副三角板按如图所示的位置摆放在直尺上,则∠1的度数为________.
三、综合题(共6题;共40分)
12.如图,三角形
中,
.
分别在
延长线上,
,
.
(1)判断
和
的位置关系,并说明理由;
(2)求
的度数.
13.证明填空:如图,已知直线
,
,
求证:
.
证明:
已知
_▲_
?
又
_▲_
?
_▲_
?
_▲
?
_▲
14.如图,
内有一点
.
(1)过点
画
交
于点
,画
交
于点
;
(2)图中不添加其它的字母,写出所有与
相等的角.
15.如图,已知AB∥CD,∠B=∠D.BE与DF平行吗?为什么?
16.如图,已知AD⊥BC于点D,EF⊥BC于点F,交AB于点G,交CA的延长线
于点E,∠E=∠AGE,求证:∠BAD=∠CAD
17.如图,已知BD⊥AC,EF⊥AC,D,F分别为垂足,G是AB上一点,且∠1=∠2.试说明:∠AGD=∠ABC.
答案解析部分
一、单选题
1.【答案】
B
【解答】如图,∵a∥b,
∴∠1=∠3=50°,
∴∠2=180°?50°=130°,
故答案为:B.
2.【答案】
B
【解答】解:如图,
∵
,
∴a∥b,
∴∠4+∠5=180°,
∵∠5=
,
∴∠4=80°.
故答案为:B.
3.【答案】
C
【解答】解:如图,由题意知:
,
,
,
,
,
,
.
故答案为:C.
4.【答案】
C
【解答】∵AC⊥b,
∴∠ACB=90°,
∵∠1=50°,
∴∠ABC=40°,
∵a∥b,
∴∠ABC=∠2=40°.
故答案为:C.
5.【答案】
B
【解答】解:如图,
第一次拐的角是∠1,第二次拐的角是∠2,由于平行前进,可以得到∠1=∠2.
故答案为:B.
二、填空题
6.【答案】
45°
【解答】解:如图:
∵a∥b,
∴∠3=∠1=45°,
∴∠2=∠3=45°.
故答案为:45°.
7.【答案】
65
【解答】解:∵a∥b
,
∴∠1=∠3,
∵∠2=115°,
∴∠3=180°﹣115°=65°(邻补角定义),
∴∠1=∠3=65°.
故答案为:65.
8.【答案】
40
【解答】解:∵∠ADE=60°,∠B=60°
∴DE∥BC
∴∠C=∠AED=40°
9.【答案】
80°
【解答】解:如图
∵
,
∴∠2=∠3,
∵∠1=2∠2,
∴∠1=2∠3,
∴∠1+∠4+∠3=180°
又依题意知∠4=60°,
∴3∠3=120°,
∴∠3=40°,
∴∠1=2∠3=80°,
故答案为:80°
10.【答案】
72°
【解答】解:如图,
∵
,
,
∴∠1=∠5,
∴c∥d,
∴∠3=∠4,
∵
,
∴
.
故答案为:72°.
11.【答案】
75
【解答】解:∵∠2+60°+45°=180°,
∴∠2=75°.
∵直尺的上下两边平行,
∴∠1=∠2=75°.
故答案为:75.
三、综合题
12.【答案】
(1)解:
.
理由如下:
,
(2)解:由(1)知,
,
∵
13.【答案】
证明:
已知
垂直的定义
又
已知
两直线平行,同位角相等
等量代换
垂直的定义
,
14.【答案】
(1)解:如图所示;
(2)解:由题意知:
,
,
∴四边形OCPD是平行四边形
∴∠O=∠PCA=∠BDP=∠CPD.
即与
相等的角有∠PCA,∠BDP,∠CPD
(2)解:∵PC∥OB,∴
∠O=∠PCA
,
∵PD∥OA,∴
∠O=∠BDP,
∠PCA=∠CPD,
∴
∠O=∠PCA=∠BDP=∠CPD
,
即与
相等的角有∠PCA,∠BDP,∠CPD
15.【答案】
解:BE与DF平行
理由:∵AB∥CD(已知)
?∴∠B=∠COE(两直线平行,同位角相等)
又∵∠B=∠D(已知)
?∴∠D=∠COE(等量代换)
?∴BE与DF平行(同位角相等,两直线平行)
16.【答案】
证明:∵AD⊥BC,EF⊥BC(已知),
∴AD∥EF(在同一平面内,垂直于同一直线的两条直线平行),
∴∠AGE=∠BAD(两直线平行,内错角相等),
∠E=∠CAD(两直线平行,同位角相等),
∵∠AGE=∠E(已知),
∴∠BAD=∠CAD(等量代换).
17.【答案】
解:∵BD⊥AC,EF⊥AC,
∴BD∥EF,∴∠DBC=∠1.
∵∠1=∠2,∴∠2=∠DBC,
∴GD∥BC,∴∠AGD=∠ABC.
21世纪教育网(www.21cnjy.com)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
初中数学浙教版七年级下册1.4
平行线的性质(1)
同步练习
一、单选题(共5题;共10分)
1.如图,已知直线
,
,则
的度数为(???
)
????????????????????????????????????B.????????????????????????????????????C.????????????????????????????????????D.?
(第1题)
(第2题)
2.如图,直线
与直线
相交,已知
,则
的度数是(?
)
A.???????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
3.如图,三角板的直角顶点落在矩形纸片的一边上.若
,则
的度数是(??
)
?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
(第3题)
(第4题)
4.如图.直线a∥b,直线L与a、b分别交于点A,B,过点A作AC⊥b于点C.若∠1=50°,则∠2的度数为(?
)
A.?130°??????????????????????????????????????B.?50°??????????????????????????????????????C.?40°??????????????????????????????????????D.?25°
5.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的角度是(?
)
A.?第一次右拐60°,第二次左拐120°
B.?第一次左拐60°,第二次右拐60°
C.?第一次左拐60°,第二次左拐120°
D.?第一次右拐60°,第二次右拐60°
二、填空题(共6题;共6分)
6.如图所示,直线a∥b,如果∠1=45°,那么∠2的度数是________.
(第6题)
(第7题)
7.已知:如图,直线a∥b
,
直线c与a
,
b相交,若∠2=115°,则∠1=________度.
8.如图,
中,
是
上一点,
是
上一点,
,
,
,则
________.
(第8题)
(第9题)
9.如图,现将一块含有30°角的直角三角板的顶点放在平行线的一条直线上,与另一条直线的夹角为∠2,若∠1=2∠2,那么∠1=________°.
10.如图,
,
,则
________.
(第10题)
(第11题)
11.将一副三角板按如图所示的位置摆放在直尺上,则∠1的度数为________.
三、综合题(共6题;共40分)
12.如图,三角形
中,
.
分别在
延长线上,
,
.
(1)判断
和
的位置关系,并说明理由;
(2)求
的度数.
13.证明填空:如图,已知直线
,
,
求证:
.
证明:
已知
_▲_
?
又
_▲_
?
_▲_
?
_▲
?
_▲
14.如图,
内有一点
.
(1)过点
画
交
于点
,画
交
于点
;
(2)图中不添加其它的字母,写出所有与
相等的角.
15.如图,已知AB∥CD,∠B=∠D.BE与DF平行吗?为什么?
16.如图,已知AD⊥BC于点D,EF⊥BC于点F,交AB于点G,交CA的延长线
于点E,∠E=∠AGE,求证:∠BAD=∠CAD
17.如图,已知BD⊥AC,EF⊥AC,D,F分别为垂足,G是AB上一点,且∠1=∠2.试说明:∠AGD=∠ABC.
答案解析部分
一、单选题
1.【答案】
B
【解答】如图,∵a∥b,
∴∠1=∠3=50°,
∴∠2=180°?50°=130°,
故答案为:B.
2.【答案】
B
【解答】解:如图,
∵
,
∴a∥b,
∴∠4+∠5=180°,
∵∠5=
,
∴∠4=80°.
故答案为:B.
3.【答案】
C
【解答】解:如图,由题意知:
,
,
,
,
,
,
.
故答案为:C.
4.【答案】
C
【解答】∵AC⊥b,
∴∠ACB=90°,
∵∠1=50°,
∴∠ABC=40°,
∵a∥b,
∴∠ABC=∠2=40°.
故答案为:C.
5.【答案】
B
【解答】解:如图,
第一次拐的角是∠1,第二次拐的角是∠2,由于平行前进,可以得到∠1=∠2.
故答案为:B.
二、填空题
6.【答案】
45°
【解答】解:如图:
∵a∥b,
∴∠3=∠1=45°,
∴∠2=∠3=45°.
故答案为:45°.
7.【答案】
65
【解答】解:∵a∥b
,
∴∠1=∠3,
∵∠2=115°,
∴∠3=180°﹣115°=65°(邻补角定义),
∴∠1=∠3=65°.
故答案为:65.
8.【答案】
40
【解答】解:∵∠ADE=60°,∠B=60°
∴DE∥BC
∴∠C=∠AED=40°
9.【答案】
80°
【解答】解:如图
∵
,
∴∠2=∠3,
∵∠1=2∠2,
∴∠1=2∠3,
∴∠1+∠4+∠3=180°
又依题意知∠4=60°,
∴3∠3=120°,
∴∠3=40°,
∴∠1=2∠3=80°,
故答案为:80°
10.【答案】
72°
【解答】解:如图,
∵
,
,
∴∠1=∠5,
∴c∥d,
∴∠3=∠4,
∵
,
∴
.
故答案为:72°.
11.【答案】
75
【解答】解:∵∠2+60°+45°=180°,
∴∠2=75°.
∵直尺的上下两边平行,
∴∠1=∠2=75°.
故答案为:75.
三、综合题
12.【答案】
(1)解:
.
理由如下:
,
(2)解:由(1)知,
,
∵
13.【答案】
证明:
已知
垂直的定义
又
已知
两直线平行,同位角相等
等量代换
垂直的定义
,
14.【答案】
(1)解:如图所示;
(2)解:由题意知:
,
,
∴四边形OCPD是平行四边形
∴∠O=∠PCA=∠BDP=∠CPD.
即与
相等的角有∠PCA,∠BDP,∠CPD
(2)解:∵PC∥OB,∴
∠O=∠PCA
,
∵PD∥OA,∴
∠O=∠BDP,
∠PCA=∠CPD,
∴
∠O=∠PCA=∠BDP=∠CPD
,
即与
相等的角有∠PCA,∠BDP,∠CPD
15.【答案】
解:BE与DF平行
理由:∵AB∥CD(已知)
?∴∠B=∠COE(两直线平行,同位角相等)
又∵∠B=∠D(已知)
?∴∠D=∠COE(等量代换)
?∴BE与DF平行(同位角相等,两直线平行)
16.【答案】
证明:∵AD⊥BC,EF⊥BC(已知),
∴AD∥EF(在同一平面内,垂直于同一直线的两条直线平行),
∴∠AGE=∠BAD(两直线平行,内错角相等),
∠E=∠CAD(两直线平行,同位角相等),
∵∠AGE=∠E(已知),
∴∠BAD=∠CAD(等量代换).
17.【答案】
解:∵BD⊥AC,EF⊥AC,
∴BD∥EF,∴∠DBC=∠1.
∵∠1=∠2,∴∠2=∠DBC,
∴GD∥BC,∴∠AGD=∠ABC.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
