1.5 图形的平移同步练习(含解析)
图片预览

文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
初中数学浙教版七年级下册1.5
图形的平移
同步练习
一、单选题(共6题;共12分)
1.下列几组图形中,通过平移后能够重合的是(???
)
A.????????????????????????B.????????????????????????C.????????????????????????D.?
2.如图所示,△DEF经过平移可以得到△ABC,那么∠C的对应角和ED的对应边分别是(??
)
?∠F,AC?????????????????????????B.?∠BOD,BA?????????????????????????C.?∠F,BA?????????????????????????D.?∠BOD,AC
(第2题)
(第4题)
3.下列现象属于数学中的平移的是(??
)
A.?树叶从树上随风飘落???????????????????????????????????????????B.?升降电梯由一楼升到顶楼
C.?汽车方向盘的转动??????????????????????????????????????????????D.?“神舟”号卫星绕地球运动
4.如图,
沿
所在的直线平移到
的位置,且
点是线段
的中点,若
,
,
,则
的长是
???
A.?5???????????????????????????????????????????B.?4???????????????????????????????????????????C.?3???????????????????????????????????????????D.?2
5.如图,将周长为18的△ABC沿BC方向平移2个单位得△DEF,则四边形ABFD的周长为(??
)
?22?????????????????????????????????????????B.?24?????????????????????????????????????????C.?26?????????????????????????????????????????D.?28
(第5题)
(第6题)
6.如图,长方形ABCD中,AB=8,第一次平移长方形ABCD沿AB的方向向右平移6个单位,得到长方形A1B1C1D1
,
第2次平移将长方形A1B1C1D1沿A1B1的方向向右平移6个单位,得到长方形A2B2C2D2
,
……第n次平移将长方形An﹣1Bn﹣1Cn﹣1Dn﹣1的方向平移6个单位,得到长方形AnBn?nDn(n>2),若ABn的长度为2018,则n的值为(??
)
A.?334??????????????????????????????????????B.?335??????????????????????????????????????C.?336??????????????????????????????????????D.?337
二、填空题(共7题;共7分)
7.如图,直径为2cm的⊙O1平移3cm到⊙O2
,
则图中阴影部分的面积为________cm2.
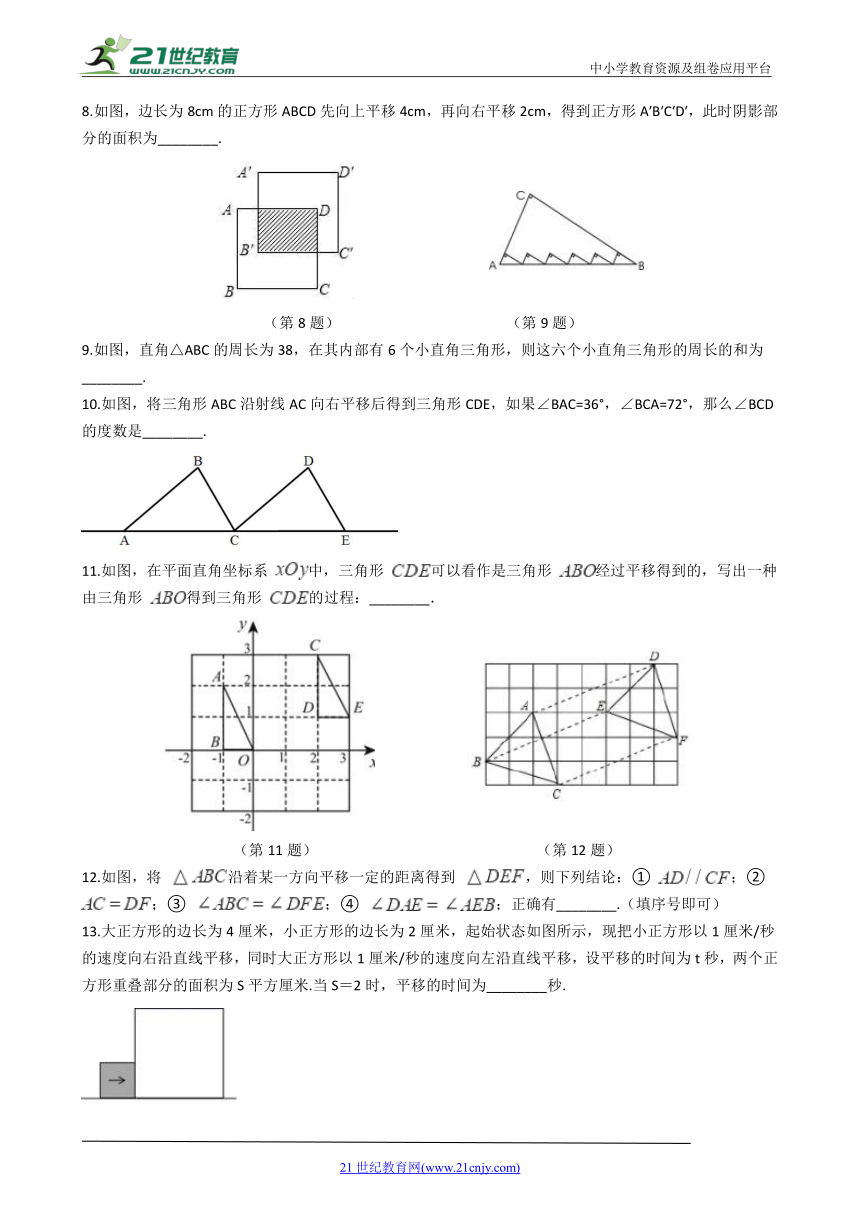
8.如图,边长为8cm的正方形ABCD先向上平移4cm,再向右平移2cm,得到正方形A′B′C′D′,此时阴影部分的面积为________.
(第8题)
(第9题)
9.如图,直角△ABC的周长为38,在其内部有6个小直角三角形,则这六个小直角三角形的周长的和为________.
10.如图,将三角形ABC沿射线AC向右平移后得到三角形CDE,如果∠BAC=36°,∠BCA=72°,那么∠BCD的度数是________.
11.如图,在平面直角坐标系
中,三角形
可以看作是三角形
经过平移得到的,写出一种由三角形
得到三角形
的过程:________.
(第11题)
(第12题)
12.如图,将
沿着某一方向平移一定的距离得到
,则下列结论:①
;②
;③
;④
;正确有________.(填序号即可)
13.大正方形的边长为4厘米,小正方形的边长为2厘米,起始状态如图所示,现把小正方形以1厘米/秒的速度向右沿直线平移,同时大正方形以1厘米/秒的速度向左沿直线平移,设平移的时间为t秒,两个正方形重叠部分的面积为S平方厘米.当S=2时,平移的时间为________秒.
三、综合题(共7题;共48分)
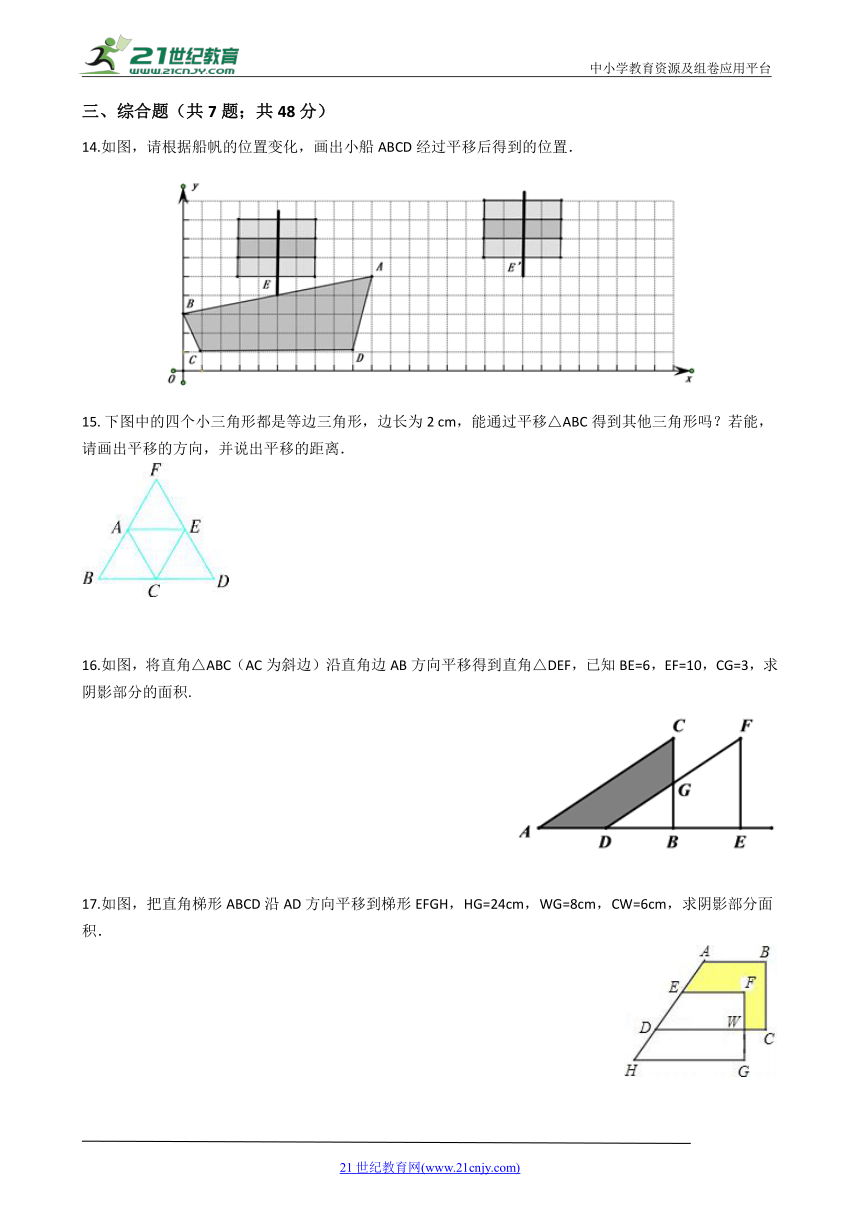
14.如图,请根据船帆的位置变化,画出小船ABCD经过平移后得到的位置.
下图中的四个小三角形都是等边三角形,边长为2
cm,能通过平移△ABC得到其他三角形吗?若能,请画出平移的方向,并说出平移的距离.
16.如图,将直角△ABC(AC为斜边)沿直角边AB方向平移得到直角△DEF,已知BE=6,EF=10,CG=3,求阴影部分的面积.
17.如图,把直角梯形ABCD沿AD方向平移到梯形EFGH,HG=24cm,WG=8cm,CW=6cm,求阴影部分面积.
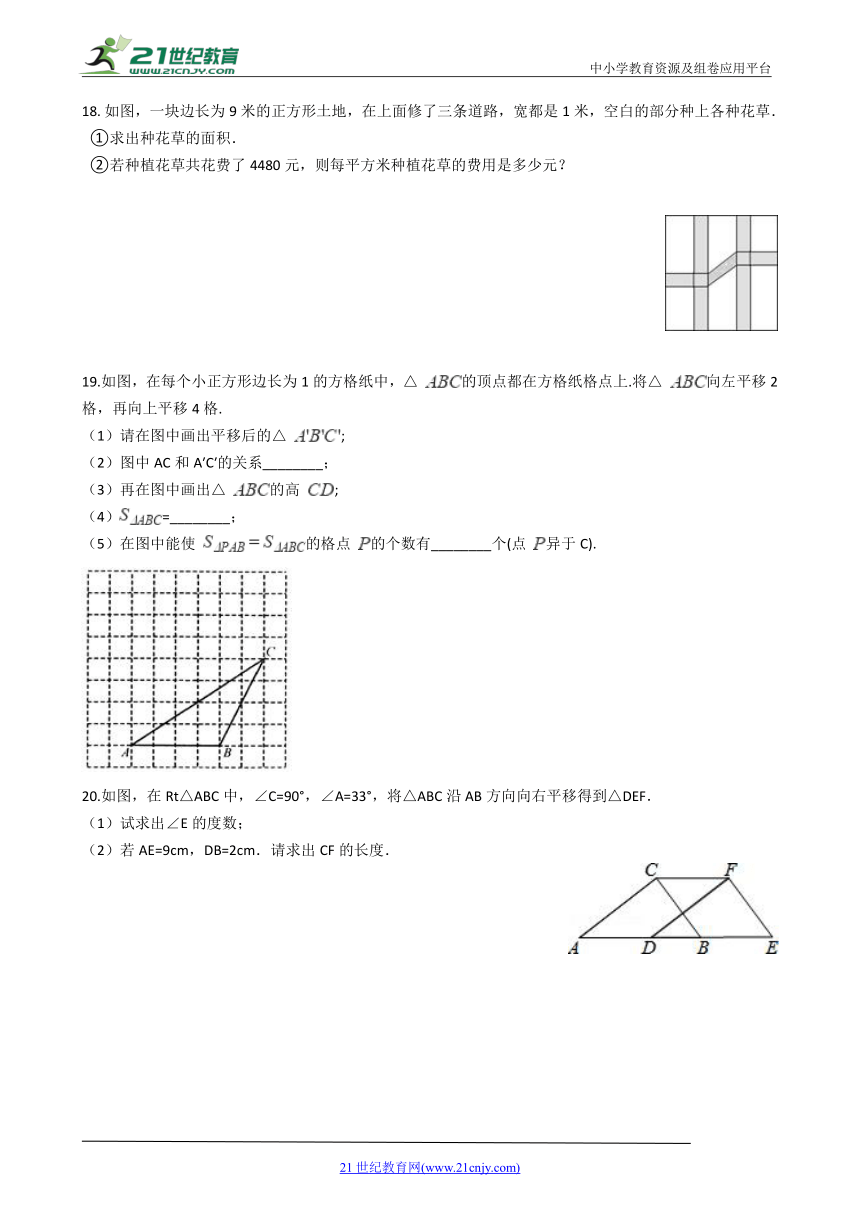
如图,一块边长为9米的正方形土地,在上面修了三条道路,宽都是1米,空白的部分种上各种花草.
①求出种花草的面积.
②若种植花草共花费了4480元,则每平方米种植花草的费用是多少元?
19.如图,在每个小正方形边长为1的方格纸中,△
的顶点都在方格纸格点上.将△
向左平移2格,再向上平移4格.
(1)请在图中画出平移后的△
;
(2)图中AC和A′C′的关系________;
(3)再在图中画出△
的高
;
(4)=________;
(5)在图中能使
的格点
的个数有________个(点
异于C).
20.如图,在Rt△ABC中,∠C=90°,∠A=33°,将△ABC沿AB方向向右平移得到△DEF.
(1)试求出∠E的度数;
(2)若AE=9cm,DB=2cm.请求出CF的长度.
答案解析部分
一、单选题
1.【答案】
D
【解答】解:A、对应点的连线相交,平移后不能重合,不符合题意;
B、两个图形大小不同,平移后不能重合,不符合题意;
C、对应点的连线相交,平移后不能重合,不符合题意;
D、平移后能重合,符合题意;
故答案为:D
.
2.【答案】
C
【解答】解:由图可知,△DEF经过平移可以得到△ABC,则AC与DF是对应边,AB与DE是对应边,BC与EF是对应边,∠A与∠EDF,∠ABC与∠E,∠C与∠F是对应角.
所以∠C的对应角和ED的对应边分别是∠F、BA.
故答案为:C.
3.【答案】
B
【解答】A.树叶从树上随风飘落,不属于平移;
B.升降电梯由一楼升到顶楼属于平移;
C.汽车方向盘的转动属于旋转;
D.
“神舟”号卫星绕地球运动属于旋转;
故答案为:B.
4.【答案】
B
【解答】解:由平移的性质可知,
,
,
,
,
,
故答案为:B.
5.【答案】
A
【解答】解:∵△ABC沿BC方向平移2个单位得到△DEF,
∴AD=CF=2,AC=DF,
∴四边形ABFD的周长=AB+(BC+CF)+DF+AD=AB+BC+AC+AD+CF,
∵△ABC的周长=18,
∴AB+BC+AC=18,
∴四边形ABFD的周长=18+2+2=22.
故答案为:A.
6.【答案】
B
【解答】∵AB=8,第1次平移将矩形ABCD沿AB的方向向右平移6个单位,得到矩形A1B1C1D1
,
第2次平移将矩形A1B1C1D1沿A1B1的方向向右平移6个单位,得到矩形A2B2C2D2…,
∴AA1=6,A1A2=6,A2B1=A1B1﹣A1A2=8﹣6=2,
∴AB1=AA1+A1A2+A2B1=6+6+2=14,
∴AB2的长为:6+6+8=20;
∵AB1=2×6+2=14,AB2=3×6+2=20,
∴ABn=(n+1)×6+2=2018,
解得:n=335.
故答案为:B.
二、填空题
7.【答案】
6
【解答】解:∵⊙O1平移3cm到⊙O2
∴⊙O1与⊙O2全等
∴图中的阴影部分的面积=图中的矩形的面积
∴图中阴影部分面积为2×3=6cm2.
故答案为:6.
8.【答案】
24cm2
【解答】解:∵边长为8cm的正方形ABCD先向上平移4cm,
∴阴影部分的宽为8﹣4=4m,
∵再向右平移2cm,
∴阴影部分的长为8﹣2=6cm,
∴阴影部分的面积为6×4=24cm2.
故答案为:24cm2.
9.【答案】
38
【解答】解:由平移的性质,6个小直角三角形较长的直角边平移后等于BC边,
较短的直角边平移后等于AC边,
斜边之和等于AB边长,
所以,6个小直角三角形的周长之和=Rt△ACB的周长,
∵直角三角形ACB的周长为38,
∴这6个小直角三角形的周长之和=38.
故答案为:38.
10.【答案】
【解答】∵三角形ABC沿射线AC向右平移后得到三角形CDE,∠BAC=36°,∴∠BAC=∠DCE=36°,又∵∠BCA=72°,∴
;故答案为
.
11.【答案】
向右平移3个单位,再向上平移1个单位得到△CDE.
【解答】解:将△ABO向右平移3个单位,再向上平移1个单位得到△CDE;
故答案为:向右平移3个单位,再向上平移1个单位得到△CDE.
12.【答案】
①②④
【解答】∵将
沿着某一方向平移一定的距离得到
,
∴
,
,
∵AD∥BE,
∴
,
故①、②、④正确,
故答案为:①②④.
13.【答案】
0.5或2.5
【解答】当
时,重叠部分长方形的宽
,
重叠部分在大正方形的左边时,
秒,
重叠部分在大正方形的右边时,t=
秒,
综上所述,小正方形平移的时间为
或
秒.
故答案为:
或
.
三、综合题
14.【答案】
如图所示.
图中,四边形A′B′C′D′即为所作.
15.【答案】解:平移△ABC得到的三角形有△AEF,△CDE.其平移方向分别是:射线AF(或射线BA或射线CE)的方向,射线AE(或射线BC或射线CD)的方向;其平移的距离均为2
cm
16.【答案】
解:依题意可得:阴影部分的面积=梯形BEFG的面积
又BE=6,EF=10,CG=3
∴BG=BC-CG=EF-CG=10-3=7
∴梯形BEFG的面积是
(BG+EF)·BE
=
=51
即所求阴影部分的面积是51.
故答案为:51.
17.【答案】
解:由平移的性质,梯形ABCD的面积=梯形EFGH的面积,CD=HG=24cm,
∴阴影部分的面积=梯形DWGH的面积,
∵CW=6cm,
∴DW=CD﹣CW=24﹣6=18cm,
∴阴影部分的面积=
(DW+HG)?WG=
(18+24)×8=168cm2
.
答:阴影部分面积是168cm2
.
18.【答案】
解:①(9-2)×(9-1)=56(平方米),∴种花草的面积为56平方米;
②4480÷56=80(元/平方米),∴
每平方米种植花草的费用
80元。
19.【答案】
(1)解:如图①所示,
(2)平行且相等
(3)解:如图①所示:过点C作线段AB的垂线,交线段AB的延长线于点D.
(4)8
(5)9
【解答】解:(2)根据平移的性质可得:AC∥A′C′,AC=A′C′;
即这两条线段之间的关系是平行且相等.
故答案为:平行且相等.
(
4
)S△ABC=
AB?CD=
×4×4=8;
故答案为:8;
(
5
)∵
,AB=4,∴点P到直线AB的距离为4,结合图形,满足条件的格点P有9个,在经过点C与直线AB平行的直线上,如图②所示,
故答案为:9
20.【答案】
(1)解:∵在Rt△ABC中,∠C=90°,∠A=33°,
∴∠CBA=90°﹣33°=57°,
由平移得,∠E=∠CBA=57°
(2)解:由平移得,AD=BE=CF,
∵AE=9cm,DB=2cm,
∴AD=BE=
×(9﹣2)=3.5cm,
∴CF=3.5cm.
21世纪教育网(www.21cnjy.com)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
初中数学浙教版七年级下册1.5
图形的平移
同步练习
一、单选题(共6题;共12分)
1.下列几组图形中,通过平移后能够重合的是(???
)
A.????????????????????????B.????????????????????????C.????????????????????????D.?
2.如图所示,△DEF经过平移可以得到△ABC,那么∠C的对应角和ED的对应边分别是(??
)
?∠F,AC?????????????????????????B.?∠BOD,BA?????????????????????????C.?∠F,BA?????????????????????????D.?∠BOD,AC
(第2题)
(第4题)
3.下列现象属于数学中的平移的是(??
)
A.?树叶从树上随风飘落???????????????????????????????????????????B.?升降电梯由一楼升到顶楼
C.?汽车方向盘的转动??????????????????????????????????????????????D.?“神舟”号卫星绕地球运动
4.如图,
沿
所在的直线平移到
的位置,且
点是线段
的中点,若
,
,
,则
的长是
???
A.?5???????????????????????????????????????????B.?4???????????????????????????????????????????C.?3???????????????????????????????????????????D.?2
5.如图,将周长为18的△ABC沿BC方向平移2个单位得△DEF,则四边形ABFD的周长为(??
)
?22?????????????????????????????????????????B.?24?????????????????????????????????????????C.?26?????????????????????????????????????????D.?28
(第5题)
(第6题)
6.如图,长方形ABCD中,AB=8,第一次平移长方形ABCD沿AB的方向向右平移6个单位,得到长方形A1B1C1D1
,
第2次平移将长方形A1B1C1D1沿A1B1的方向向右平移6个单位,得到长方形A2B2C2D2
,
……第n次平移将长方形An﹣1Bn﹣1Cn﹣1Dn﹣1的方向平移6个单位,得到长方形AnBn?nDn(n>2),若ABn的长度为2018,则n的值为(??
)
A.?334??????????????????????????????????????B.?335??????????????????????????????????????C.?336??????????????????????????????????????D.?337
二、填空题(共7题;共7分)
7.如图,直径为2cm的⊙O1平移3cm到⊙O2
,
则图中阴影部分的面积为________cm2.
8.如图,边长为8cm的正方形ABCD先向上平移4cm,再向右平移2cm,得到正方形A′B′C′D′,此时阴影部分的面积为________.
(第8题)
(第9题)
9.如图,直角△ABC的周长为38,在其内部有6个小直角三角形,则这六个小直角三角形的周长的和为________.
10.如图,将三角形ABC沿射线AC向右平移后得到三角形CDE,如果∠BAC=36°,∠BCA=72°,那么∠BCD的度数是________.
11.如图,在平面直角坐标系
中,三角形
可以看作是三角形
经过平移得到的,写出一种由三角形
得到三角形
的过程:________.
(第11题)
(第12题)
12.如图,将
沿着某一方向平移一定的距离得到
,则下列结论:①
;②
;③
;④
;正确有________.(填序号即可)
13.大正方形的边长为4厘米,小正方形的边长为2厘米,起始状态如图所示,现把小正方形以1厘米/秒的速度向右沿直线平移,同时大正方形以1厘米/秒的速度向左沿直线平移,设平移的时间为t秒,两个正方形重叠部分的面积为S平方厘米.当S=2时,平移的时间为________秒.
三、综合题(共7题;共48分)
14.如图,请根据船帆的位置变化,画出小船ABCD经过平移后得到的位置.
下图中的四个小三角形都是等边三角形,边长为2
cm,能通过平移△ABC得到其他三角形吗?若能,请画出平移的方向,并说出平移的距离.
16.如图,将直角△ABC(AC为斜边)沿直角边AB方向平移得到直角△DEF,已知BE=6,EF=10,CG=3,求阴影部分的面积.
17.如图,把直角梯形ABCD沿AD方向平移到梯形EFGH,HG=24cm,WG=8cm,CW=6cm,求阴影部分面积.
如图,一块边长为9米的正方形土地,在上面修了三条道路,宽都是1米,空白的部分种上各种花草.
①求出种花草的面积.
②若种植花草共花费了4480元,则每平方米种植花草的费用是多少元?
19.如图,在每个小正方形边长为1的方格纸中,△
的顶点都在方格纸格点上.将△
向左平移2格,再向上平移4格.
(1)请在图中画出平移后的△
;
(2)图中AC和A′C′的关系________;
(3)再在图中画出△
的高
;
(4)=________;
(5)在图中能使
的格点
的个数有________个(点
异于C).
20.如图,在Rt△ABC中,∠C=90°,∠A=33°,将△ABC沿AB方向向右平移得到△DEF.
(1)试求出∠E的度数;
(2)若AE=9cm,DB=2cm.请求出CF的长度.
答案解析部分
一、单选题
1.【答案】
D
【解答】解:A、对应点的连线相交,平移后不能重合,不符合题意;
B、两个图形大小不同,平移后不能重合,不符合题意;
C、对应点的连线相交,平移后不能重合,不符合题意;
D、平移后能重合,符合题意;
故答案为:D
.
2.【答案】
C
【解答】解:由图可知,△DEF经过平移可以得到△ABC,则AC与DF是对应边,AB与DE是对应边,BC与EF是对应边,∠A与∠EDF,∠ABC与∠E,∠C与∠F是对应角.
所以∠C的对应角和ED的对应边分别是∠F、BA.
故答案为:C.
3.【答案】
B
【解答】A.树叶从树上随风飘落,不属于平移;
B.升降电梯由一楼升到顶楼属于平移;
C.汽车方向盘的转动属于旋转;
D.
“神舟”号卫星绕地球运动属于旋转;
故答案为:B.
4.【答案】
B
【解答】解:由平移的性质可知,
,
,
,
,
,
故答案为:B.
5.【答案】
A
【解答】解:∵△ABC沿BC方向平移2个单位得到△DEF,
∴AD=CF=2,AC=DF,
∴四边形ABFD的周长=AB+(BC+CF)+DF+AD=AB+BC+AC+AD+CF,
∵△ABC的周长=18,
∴AB+BC+AC=18,
∴四边形ABFD的周长=18+2+2=22.
故答案为:A.
6.【答案】
B
【解答】∵AB=8,第1次平移将矩形ABCD沿AB的方向向右平移6个单位,得到矩形A1B1C1D1
,
第2次平移将矩形A1B1C1D1沿A1B1的方向向右平移6个单位,得到矩形A2B2C2D2…,
∴AA1=6,A1A2=6,A2B1=A1B1﹣A1A2=8﹣6=2,
∴AB1=AA1+A1A2+A2B1=6+6+2=14,
∴AB2的长为:6+6+8=20;
∵AB1=2×6+2=14,AB2=3×6+2=20,
∴ABn=(n+1)×6+2=2018,
解得:n=335.
故答案为:B.
二、填空题
7.【答案】
6
【解答】解:∵⊙O1平移3cm到⊙O2
∴⊙O1与⊙O2全等
∴图中的阴影部分的面积=图中的矩形的面积
∴图中阴影部分面积为2×3=6cm2.
故答案为:6.
8.【答案】
24cm2
【解答】解:∵边长为8cm的正方形ABCD先向上平移4cm,
∴阴影部分的宽为8﹣4=4m,
∵再向右平移2cm,
∴阴影部分的长为8﹣2=6cm,
∴阴影部分的面积为6×4=24cm2.
故答案为:24cm2.
9.【答案】
38
【解答】解:由平移的性质,6个小直角三角形较长的直角边平移后等于BC边,
较短的直角边平移后等于AC边,
斜边之和等于AB边长,
所以,6个小直角三角形的周长之和=Rt△ACB的周长,
∵直角三角形ACB的周长为38,
∴这6个小直角三角形的周长之和=38.
故答案为:38.
10.【答案】
【解答】∵三角形ABC沿射线AC向右平移后得到三角形CDE,∠BAC=36°,∴∠BAC=∠DCE=36°,又∵∠BCA=72°,∴
;故答案为
.
11.【答案】
向右平移3个单位,再向上平移1个单位得到△CDE.
【解答】解:将△ABO向右平移3个单位,再向上平移1个单位得到△CDE;
故答案为:向右平移3个单位,再向上平移1个单位得到△CDE.
12.【答案】
①②④
【解答】∵将
沿着某一方向平移一定的距离得到
,
∴
,
,
∵AD∥BE,
∴
,
故①、②、④正确,
故答案为:①②④.
13.【答案】
0.5或2.5
【解答】当
时,重叠部分长方形的宽
,
重叠部分在大正方形的左边时,
秒,
重叠部分在大正方形的右边时,t=
秒,
综上所述,小正方形平移的时间为
或
秒.
故答案为:
或
.
三、综合题
14.【答案】
如图所示.
图中,四边形A′B′C′D′即为所作.
15.【答案】解:平移△ABC得到的三角形有△AEF,△CDE.其平移方向分别是:射线AF(或射线BA或射线CE)的方向,射线AE(或射线BC或射线CD)的方向;其平移的距离均为2
cm
16.【答案】
解:依题意可得:阴影部分的面积=梯形BEFG的面积
又BE=6,EF=10,CG=3
∴BG=BC-CG=EF-CG=10-3=7
∴梯形BEFG的面积是
(BG+EF)·BE
=
=51
即所求阴影部分的面积是51.
故答案为:51.
17.【答案】
解:由平移的性质,梯形ABCD的面积=梯形EFGH的面积,CD=HG=24cm,
∴阴影部分的面积=梯形DWGH的面积,
∵CW=6cm,
∴DW=CD﹣CW=24﹣6=18cm,
∴阴影部分的面积=
(DW+HG)?WG=
(18+24)×8=168cm2
.
答:阴影部分面积是168cm2
.
18.【答案】
解:①(9-2)×(9-1)=56(平方米),∴种花草的面积为56平方米;
②4480÷56=80(元/平方米),∴
每平方米种植花草的费用
80元。
19.【答案】
(1)解:如图①所示,
(2)平行且相等
(3)解:如图①所示:过点C作线段AB的垂线,交线段AB的延长线于点D.
(4)8
(5)9
【解答】解:(2)根据平移的性质可得:AC∥A′C′,AC=A′C′;
即这两条线段之间的关系是平行且相等.
故答案为:平行且相等.
(
4
)S△ABC=
AB?CD=
×4×4=8;
故答案为:8;
(
5
)∵
,AB=4,∴点P到直线AB的距离为4,结合图形,满足条件的格点P有9个,在经过点C与直线AB平行的直线上,如图②所示,
故答案为:9
20.【答案】
(1)解:∵在Rt△ABC中,∠C=90°,∠A=33°,
∴∠CBA=90°﹣33°=57°,
由平移得,∠E=∠CBA=57°
(2)解:由平移得,AD=BE=CF,
∵AE=9cm,DB=2cm,
∴AD=BE=
×(9﹣2)=3.5cm,
∴CF=3.5cm.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
