2.4 二元一次方程组的应用同步练习(含解析)
文档属性
| 名称 | 2.4 二元一次方程组的应用同步练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 255.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 09:01:37 | ||
图片预览



文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
初中数学浙教版七年级下册2.4
二元一次方程组的应用
同步练习
一、单选题(共6题;共12分)
1.已知a,b满足方程组
,则a+b的值为(???
)
A.?-4??????????????????????????????????????????B.?4??????????????????????????????????????????C.?-2??????????????????????????????????????????D.?2
2.篮球比赛中,每场比赛都要分出胜负,每队胜1场得3分,负一场扣1分,某队在8场比赛中得到12分,若设该队胜的场数为
,负的场数为
,则可列出方程组(??
)
A.?????????????????????B.?????????????????????C.?????????????????????D.?
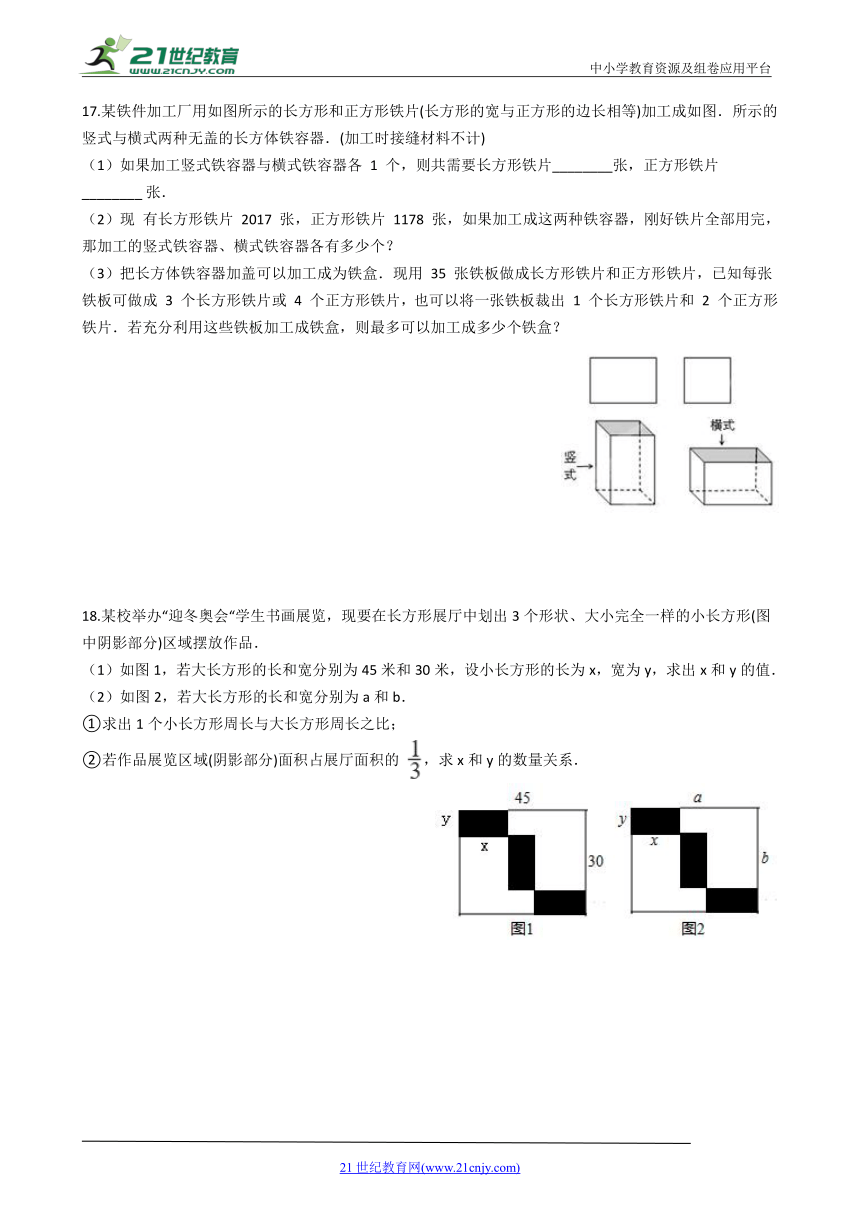
3.欣欣幼儿园购买了90张等边三角形彩纸与50张正方形彩纸(如图1),准备制作如图2所示的甲、乙两种图案,如果购买的彩纸刚好全部用完,则可以制作甲、乙两种图案共(???
)
A.?10个????????????????????????????????????B.?20个????????????????????????????????????C.?30个????????????????????????????????????D.?40个
4.6年前,A的年龄是B的3倍,现在A的年龄是B的2倍,A现在的年龄是(???
)岁。
A.???
12????????????????????????????????????????B.?18????????????????????????????????????????C.?24????????????????????????????????????????D.?30
5.《九章算术》是我国东汉初年编订的一部数学经典著作。在它的“方程”一章里,一次方程组是由算筹布置而成的,《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1、图2,图中各行从左到右列出的算筹数分别表示未知数x
,
y的系数与相应的常数项,把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是:
,类似地,图2所示的算筹图我们可以表述为(?
)
A.??????????????????B.??????????????????C.??????????????????D.?
6.如图,由10个大小一样的小长方形组成的大长方形的周长为78,则每一个小长方形的面积是(??
)
A.?18?????????????????????????????????????????B.?24?????????????????????????????????????????C.?36?????????????????????????????????????????D.?48
二、填空题(共6题;共8分)
7.某校运动员分组训练,若每组7人,余3人;若每组8人,则缺5人;设运动员人数为x人,组数为y组,则列方程组为________.
8.某营业员昨天卖出7件衬衫和4条裤子共460元,今天又卖出9件衬衫和6条裤子共660元,则每件衬衫售价为________,每条裤子售价为________。
9.甲、乙两人练习跑步,如果乙先跑10米,则甲跑5秒就可追上乙;如果乙先跑2秒,则甲跑4秒就可追上乙,若设甲的速度为x米/秒,乙的速度为y米/秒,可列方程组________.
10.一个两位数的数字之和是7,这个两位数减去27,它的十位和个位上的数字就交换了位置,则这个两位数是?________?
11.三位先生A,B,C带着他们的妻子a、b、c到超市购物,至于谁是谁的妻子现在只能从下列条件来推测:他们6人,每人花在买商品的钱数(单位:元)正好等于商品数量的平方,而且每位先生都比自己的妻子多花48元钱,又知先生A比b多买9件商品,先生B比a多买7件商品,则先生A的妻子是________。
12.??2019年的《最强大脑》节目中,有很多具有挑战性的比赛项目,其中《幻圆》这个项目充分体现了数学的魅力.如图是一个最简单的二阶幻圆的模型,要求:①内、外两个圆周上的四个数字之和相等;②外圆两直径上的四个数字之和相等,则图中两空白圆圈内应填写的数字从左到右依次为________和________。
三、综合题(共6题;共58分)
13.确保室内空气新鲜,一方面是提高生活质量的需要,另一方面也是有效防控新型冠状病毒传播的需要,因而越来越多的居民选购家用空气净化器以净化室内空气。阳光商场抓住商机,从厂家购进了A、B两种型号的净化器共160台,A型号净化器进价是1500元/台,B型号净化器进价是3500元/台,购进两种型号净化器共用去360000元。
(1)求商场各进了A、B两种型号的净化器多少台?
(2)为使每台B型号净化器的毛利润是A型号的2倍,且保证售完这160台净化器的毛利润达到110000元,求每台A型号净化器的售价。(注:
毛利润=售价-进价)
14.随着中国传统节日“端午节”的临近,某超市决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元。
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?
(2)百叶龙敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?
15.一条高铁线A,B,C三个车站的位置如图所示.已知B,C两站之间相距530千米.高铁列车从B站出发,向C站方向匀速行驶,经过13分钟距A站165千米;经过80分钟距A站500千米.
(1)求高铁列车的速度和AB两站之间的距离.
(2)如果高铁列车从A站出发,开出多久可以到达C站?
16.滴滴快车是一种便捷的出行工具,计价规则如下表:
(1)若小林乘车9千米,耗时30分钟,则车费是________元.
(2)小王与小林各自乘坐滴滴快车,行车里程共15千米,其中小王乘车里程少于7公里,乘车时间比小林多10分钟。如果下车时所付车费相同,两人共支付43.2元·求小王的乘车里程数和乘车时间.
计费项目
里程费
时长费
运途费
单价
2元/千米
0.4元/分钟
1元/千米
注:
1.车费=里程费+时长费+运途费
2.里程费按行车实际里程计费:时长费按行车实际时间计算,运途费收取标准为:行车7千米以内(含7千米)不收费:若超过7千米,则超出部分每千米加收1元.
17.某铁件加工厂用如图所示的长方形和正方形铁片(长方形的宽与正方形的边长相等)加工成如图.所示的竖式与横式两种无盖的长方体铁容器.(加工时接缝材料不计)
(1)如果加工竖式铁容器与横式铁容器各
1
个,则共需要长方形铁片________张,正方形铁片________?张.
(2)现
有长方形铁片
2017
张,正方形铁片
1178
张,如果加工成这两种铁容器,刚好铁片全部用完,那加工的竖式铁容器、横式铁容器各有多少个?
(3)把长方体铁容器加盖可以加工成为铁盒.现用
35
张铁板做成长方形铁片和正方形铁片,已知每张铁板可做成
3
个长方形铁片或
4
个正方形铁片,也可以将一张铁板裁出
1
个长方形铁片和
2
个正方形铁片.若充分利用这些铁板加工成铁盒,则最多可以加工成多少个铁盒?
18.某校举办“迎冬奥会“学生书画展览,现要在长方形展厅中划出3个形状、大小完全一样的小长方形(图中阴影部分)区域摆放作品.
(1)如图1,若大长方形的长和宽分别为45米和30米,设小长方形的长为x,宽为y,求出x和y的值.
(2)如图2,若大长方形的长和宽分别为a和b.
①求出1个小长方形周长与大长方形周长之比;
②若作品展览区域(阴影部分)面积占展厅面积的
,求x和y的数量关系.
答案解析部分
一、单选题
1.【答案】
D
【解答】解:
①+②得:7a+7b=14
解得:a+b=2
故答案为:D
?2.【答案】
A
【解答】解:设该队胜的场数为x,负的场数为y,根据题意得
故答案为:A.
3.【答案】
C
【解答】解:设制作甲型图案x个,乙型图案y个,
由题意可得,
解得
所以
制作甲、乙两种图案共10+20=30(个).
故答案为:C.
4.【答案】
C
【解答】解:设A现在的年龄是x岁,B是y岁。
则6年前A是(x-6)岁,B是(y-6)岁,
则
解得
故答案为:C。
5.【答案】
A
【解答】第一个方程,算筹数分别是2,1,右边的是11;第二个方程,算筹数分别是4,3,右边的是27.
则
故选A.
6.【答案】
C
【解答】解:由图形得,
解得,
∴
每一个小长方形的面积为xy=12×3=36.
故答案为:C.
二、填空题
7.【答案】
【解答】解:设运动员人数为x人,组数为y组,
由题意得:
,
故答案为:
.
8.【答案】
20;80
【解答】解:设每件衬衫的售价为x元,每条裤子的售价为y元,
依题意,得:
解得:
故答案为:20:80。
9.【答案】
【解答】解:根据乙先跑10米,则甲跑5秒就可以追上乙,得方程5x=5y+10;
根据乙先跑2秒,则甲跑4秒就可追上乙,得方程4x=4y+2y.
可得方程组
.
故答案为:
.
10.【答案】52
解:设个位数上的数字为x,十位数上的数字为y
则①
??????????????????????????????????????
?
②
①②联立解得x=2,y=5.
答:这个两位数是52.
11.【答案】
c
【解答】解:设一对夫妻,丈夫买了x件商品,妻子买了y件商品.
则有x2?y2=48,即(x十y)(x?y)=48.(4分)
∵x、y都是正整数,且x+y与x?y有相同的奇偶性,
又∵x+y>x?y,48=24×2=12×4=8×6,
∴或或
解之:或或
符合x?y=9的只有一种,可见A买了13件商品,b买了4件.
同时符合x?y=7的也只有一种,可知B买了8件,a买了1件.
∴C买了7件,c买了11件.
由此可知三对夫妻的组合是:A、c;B、b;C、a.
故答案为:c.
12.【答案】
2;9
【解答】设外圆空白处的数字为x,
内圆空白处的数字为y,
则x+3+y+11=4+6+7+8,
6+3+7+y=4+x+8+11,
即x+y=11,
x-y=-7,
解得x=2
,y=9.
故答案为:2,
9.
三、综合题
13.【答案】
(1)解:设A型号净化器购进了x台,B型号净化器购进了y台,
由题意得:
,
解得:
.
答:A型号净化器购进了100台,B型号净化器购进了60台。
(2)解:设每台A型号净化器的毛利润是
元,则每台B型号净化器的毛利润是
元,
由题意得:
,解得:
.
所以1500+500=2000(元).
答:每台A型号净化器的售价至少是2000元。
14.【答案】
(1)解:设打折前甲品牌粽子每盒x元,乙品牌粽子每盒y元,
据题意得:
?
解得:
?
答:打折前甲品牌棕子每盒70元,乙品牌粽子每盒80元.
(2)解:80×70×(1-80%)+100×80×(1-75%)=3120(元).
答:打折后购买这批粽子比不打折节省了3120元。
15.【答案】
(1)解:设高铁列车的速度为x千米/小时,AB两站之间的距离为y千米.
由题意得
,
解得
答:高铁列车的速度为300千米/小时,AB两站之间的距离为100千米.
(2)解:
.
答:
高铁列车从A站出发,开出2.1小时可以到达C站.
16.【答案】
(1)32
(2)解:设小王乘车x公里,则小林乘车里程是(15-x)公里,小王乘车时间y分钟,则小张乘车时间是(y-10)分钟,
则
化简得
解得
故小王乘车的里程数为千米,乘车时间为20分钟.
【解答】(1)
车费
=9×2+30×0.4+(9-7)×1=32(元);
17.【答案】
(1)7;3
(2)解:设加工的竖式铁容器有x个,横式铁容器各有y个,由题意得
解得
故加工的竖式铁容器有100个,横式铁容器各有539个.
(3)解:设做长方形铁片的铁板m张,做正方形铁片的铁板n张,由题意得
解得
∴在这35张铁板中,25张做长方形铁片可做
(片),9张做正方形铁片可做
(片),剩1张可裁出1个长方形铁片和2个正方形铁片
共可做长方形铁片
(片),正方形铁片
(片)
∴可做铁盒
(个)
答:最多可加工铁盒19个.
【解答】解:(1)如图,加工1个竖式铁容器需要长方形铁片4张,正方形铁片1
张;加工1个横式铁容器需要长方形铁片3张,正方形铁片2
张.
故如果加工竖式铁容器与横式铁容器各
1
个,则共需要长方形铁片7张,正方形铁片3张.
18.【答案】
(1)解:根据题意得
,……2分得
(2)解:①
①+②,得
3(x+y)=a+b,
∴
∴1个小长方形周长与大长方形周长之比是
即1个小长方形周长与大长方形周长之比是1:3;
②∵作品展览区域(阴影部分)面积占展厅面积的
∴3xy=
ab
∴3xy=
(2x+y)(x+2y),
∴(2x+y)(x+2y)=9xy
化简,得
(x-y)2=0
∴x-y=0
∴x=y
21世纪教育网(www.21cnjy.com)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
初中数学浙教版七年级下册2.4
二元一次方程组的应用
同步练习
一、单选题(共6题;共12分)
1.已知a,b满足方程组
,则a+b的值为(???
)
A.?-4??????????????????????????????????????????B.?4??????????????????????????????????????????C.?-2??????????????????????????????????????????D.?2
2.篮球比赛中,每场比赛都要分出胜负,每队胜1场得3分,负一场扣1分,某队在8场比赛中得到12分,若设该队胜的场数为
,负的场数为
,则可列出方程组(??
)
A.?????????????????????B.?????????????????????C.?????????????????????D.?
3.欣欣幼儿园购买了90张等边三角形彩纸与50张正方形彩纸(如图1),准备制作如图2所示的甲、乙两种图案,如果购买的彩纸刚好全部用完,则可以制作甲、乙两种图案共(???
)
A.?10个????????????????????????????????????B.?20个????????????????????????????????????C.?30个????????????????????????????????????D.?40个
4.6年前,A的年龄是B的3倍,现在A的年龄是B的2倍,A现在的年龄是(???
)岁。
A.???
12????????????????????????????????????????B.?18????????????????????????????????????????C.?24????????????????????????????????????????D.?30
5.《九章算术》是我国东汉初年编订的一部数学经典著作。在它的“方程”一章里,一次方程组是由算筹布置而成的,《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1、图2,图中各行从左到右列出的算筹数分别表示未知数x
,
y的系数与相应的常数项,把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是:
,类似地,图2所示的算筹图我们可以表述为(?
)
A.??????????????????B.??????????????????C.??????????????????D.?
6.如图,由10个大小一样的小长方形组成的大长方形的周长为78,则每一个小长方形的面积是(??
)
A.?18?????????????????????????????????????????B.?24?????????????????????????????????????????C.?36?????????????????????????????????????????D.?48
二、填空题(共6题;共8分)
7.某校运动员分组训练,若每组7人,余3人;若每组8人,则缺5人;设运动员人数为x人,组数为y组,则列方程组为________.
8.某营业员昨天卖出7件衬衫和4条裤子共460元,今天又卖出9件衬衫和6条裤子共660元,则每件衬衫售价为________,每条裤子售价为________。
9.甲、乙两人练习跑步,如果乙先跑10米,则甲跑5秒就可追上乙;如果乙先跑2秒,则甲跑4秒就可追上乙,若设甲的速度为x米/秒,乙的速度为y米/秒,可列方程组________.
10.一个两位数的数字之和是7,这个两位数减去27,它的十位和个位上的数字就交换了位置,则这个两位数是?________?
11.三位先生A,B,C带着他们的妻子a、b、c到超市购物,至于谁是谁的妻子现在只能从下列条件来推测:他们6人,每人花在买商品的钱数(单位:元)正好等于商品数量的平方,而且每位先生都比自己的妻子多花48元钱,又知先生A比b多买9件商品,先生B比a多买7件商品,则先生A的妻子是________。
12.??2019年的《最强大脑》节目中,有很多具有挑战性的比赛项目,其中《幻圆》这个项目充分体现了数学的魅力.如图是一个最简单的二阶幻圆的模型,要求:①内、外两个圆周上的四个数字之和相等;②外圆两直径上的四个数字之和相等,则图中两空白圆圈内应填写的数字从左到右依次为________和________。
三、综合题(共6题;共58分)
13.确保室内空气新鲜,一方面是提高生活质量的需要,另一方面也是有效防控新型冠状病毒传播的需要,因而越来越多的居民选购家用空气净化器以净化室内空气。阳光商场抓住商机,从厂家购进了A、B两种型号的净化器共160台,A型号净化器进价是1500元/台,B型号净化器进价是3500元/台,购进两种型号净化器共用去360000元。
(1)求商场各进了A、B两种型号的净化器多少台?
(2)为使每台B型号净化器的毛利润是A型号的2倍,且保证售完这160台净化器的毛利润达到110000元,求每台A型号净化器的售价。(注:
毛利润=售价-进价)
14.随着中国传统节日“端午节”的临近,某超市决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元。
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?
(2)百叶龙敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?
15.一条高铁线A,B,C三个车站的位置如图所示.已知B,C两站之间相距530千米.高铁列车从B站出发,向C站方向匀速行驶,经过13分钟距A站165千米;经过80分钟距A站500千米.
(1)求高铁列车的速度和AB两站之间的距离.
(2)如果高铁列车从A站出发,开出多久可以到达C站?
16.滴滴快车是一种便捷的出行工具,计价规则如下表:
(1)若小林乘车9千米,耗时30分钟,则车费是________元.
(2)小王与小林各自乘坐滴滴快车,行车里程共15千米,其中小王乘车里程少于7公里,乘车时间比小林多10分钟。如果下车时所付车费相同,两人共支付43.2元·求小王的乘车里程数和乘车时间.
计费项目
里程费
时长费
运途费
单价
2元/千米
0.4元/分钟
1元/千米
注:
1.车费=里程费+时长费+运途费
2.里程费按行车实际里程计费:时长费按行车实际时间计算,运途费收取标准为:行车7千米以内(含7千米)不收费:若超过7千米,则超出部分每千米加收1元.
17.某铁件加工厂用如图所示的长方形和正方形铁片(长方形的宽与正方形的边长相等)加工成如图.所示的竖式与横式两种无盖的长方体铁容器.(加工时接缝材料不计)
(1)如果加工竖式铁容器与横式铁容器各
1
个,则共需要长方形铁片________张,正方形铁片________?张.
(2)现
有长方形铁片
2017
张,正方形铁片
1178
张,如果加工成这两种铁容器,刚好铁片全部用完,那加工的竖式铁容器、横式铁容器各有多少个?
(3)把长方体铁容器加盖可以加工成为铁盒.现用
35
张铁板做成长方形铁片和正方形铁片,已知每张铁板可做成
3
个长方形铁片或
4
个正方形铁片,也可以将一张铁板裁出
1
个长方形铁片和
2
个正方形铁片.若充分利用这些铁板加工成铁盒,则最多可以加工成多少个铁盒?
18.某校举办“迎冬奥会“学生书画展览,现要在长方形展厅中划出3个形状、大小完全一样的小长方形(图中阴影部分)区域摆放作品.
(1)如图1,若大长方形的长和宽分别为45米和30米,设小长方形的长为x,宽为y,求出x和y的值.
(2)如图2,若大长方形的长和宽分别为a和b.
①求出1个小长方形周长与大长方形周长之比;
②若作品展览区域(阴影部分)面积占展厅面积的
,求x和y的数量关系.
答案解析部分
一、单选题
1.【答案】
D
【解答】解:
①+②得:7a+7b=14
解得:a+b=2
故答案为:D
?2.【答案】
A
【解答】解:设该队胜的场数为x,负的场数为y,根据题意得
故答案为:A.
3.【答案】
C
【解答】解:设制作甲型图案x个,乙型图案y个,
由题意可得,
解得
所以
制作甲、乙两种图案共10+20=30(个).
故答案为:C.
4.【答案】
C
【解答】解:设A现在的年龄是x岁,B是y岁。
则6年前A是(x-6)岁,B是(y-6)岁,
则
解得
故答案为:C。
5.【答案】
A
【解答】第一个方程,算筹数分别是2,1,右边的是11;第二个方程,算筹数分别是4,3,右边的是27.
则
故选A.
6.【答案】
C
【解答】解:由图形得,
解得,
∴
每一个小长方形的面积为xy=12×3=36.
故答案为:C.
二、填空题
7.【答案】
【解答】解:设运动员人数为x人,组数为y组,
由题意得:
,
故答案为:
.
8.【答案】
20;80
【解答】解:设每件衬衫的售价为x元,每条裤子的售价为y元,
依题意,得:
解得:
故答案为:20:80。
9.【答案】
【解答】解:根据乙先跑10米,则甲跑5秒就可以追上乙,得方程5x=5y+10;
根据乙先跑2秒,则甲跑4秒就可追上乙,得方程4x=4y+2y.
可得方程组
.
故答案为:
.
10.【答案】52
解:设个位数上的数字为x,十位数上的数字为y
则①
??????????????????????????????????????
?
②
①②联立解得x=2,y=5.
答:这个两位数是52.
11.【答案】
c
【解答】解:设一对夫妻,丈夫买了x件商品,妻子买了y件商品.
则有x2?y2=48,即(x十y)(x?y)=48.(4分)
∵x、y都是正整数,且x+y与x?y有相同的奇偶性,
又∵x+y>x?y,48=24×2=12×4=8×6,
∴或或
解之:或或
符合x?y=9的只有一种,可见A买了13件商品,b买了4件.
同时符合x?y=7的也只有一种,可知B买了8件,a买了1件.
∴C买了7件,c买了11件.
由此可知三对夫妻的组合是:A、c;B、b;C、a.
故答案为:c.
12.【答案】
2;9
【解答】设外圆空白处的数字为x,
内圆空白处的数字为y,
则x+3+y+11=4+6+7+8,
6+3+7+y=4+x+8+11,
即x+y=11,
x-y=-7,
解得x=2
,y=9.
故答案为:2,
9.
三、综合题
13.【答案】
(1)解:设A型号净化器购进了x台,B型号净化器购进了y台,
由题意得:
,
解得:
.
答:A型号净化器购进了100台,B型号净化器购进了60台。
(2)解:设每台A型号净化器的毛利润是
元,则每台B型号净化器的毛利润是
元,
由题意得:
,解得:
.
所以1500+500=2000(元).
答:每台A型号净化器的售价至少是2000元。
14.【答案】
(1)解:设打折前甲品牌粽子每盒x元,乙品牌粽子每盒y元,
据题意得:
?
解得:
?
答:打折前甲品牌棕子每盒70元,乙品牌粽子每盒80元.
(2)解:80×70×(1-80%)+100×80×(1-75%)=3120(元).
答:打折后购买这批粽子比不打折节省了3120元。
15.【答案】
(1)解:设高铁列车的速度为x千米/小时,AB两站之间的距离为y千米.
由题意得
,
解得
答:高铁列车的速度为300千米/小时,AB两站之间的距离为100千米.
(2)解:
.
答:
高铁列车从A站出发,开出2.1小时可以到达C站.
16.【答案】
(1)32
(2)解:设小王乘车x公里,则小林乘车里程是(15-x)公里,小王乘车时间y分钟,则小张乘车时间是(y-10)分钟,
则
化简得
解得
故小王乘车的里程数为千米,乘车时间为20分钟.
【解答】(1)
车费
=9×2+30×0.4+(9-7)×1=32(元);
17.【答案】
(1)7;3
(2)解:设加工的竖式铁容器有x个,横式铁容器各有y个,由题意得
解得
故加工的竖式铁容器有100个,横式铁容器各有539个.
(3)解:设做长方形铁片的铁板m张,做正方形铁片的铁板n张,由题意得
解得
∴在这35张铁板中,25张做长方形铁片可做
(片),9张做正方形铁片可做
(片),剩1张可裁出1个长方形铁片和2个正方形铁片
共可做长方形铁片
(片),正方形铁片
(片)
∴可做铁盒
(个)
答:最多可加工铁盒19个.
【解答】解:(1)如图,加工1个竖式铁容器需要长方形铁片4张,正方形铁片1
张;加工1个横式铁容器需要长方形铁片3张,正方形铁片2
张.
故如果加工竖式铁容器与横式铁容器各
1
个,则共需要长方形铁片7张,正方形铁片3张.
18.【答案】
(1)解:根据题意得
,……2分得
(2)解:①
①+②,得
3(x+y)=a+b,
∴
∴1个小长方形周长与大长方形周长之比是
即1个小长方形周长与大长方形周长之比是1:3;
②∵作品展览区域(阴影部分)面积占展厅面积的
∴3xy=
ab
∴3xy=
(2x+y)(x+2y),
∴(2x+y)(x+2y)=9xy
化简,得
(x-y)2=0
∴x-y=0
∴x=y
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
