【单元培优卷】第2章 二元一次方程 (含解析)
文档属性
| 名称 | 【单元培优卷】第2章 二元一次方程 (含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-28 13:14:27 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2020-2021学年浙教版七年级下册数学
单元测评培优卷(原版+解析版)
第2章二元一次方程
(测试时间:120分钟,满分:120分)
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020·江苏七年级月考)下列方程中,是二元一次方程的(
)
A.
B.
C.
D.
2.(2020·浙江七年级)解方程组时,①—②,得(
)
A.
.
B.
C.
D.
3.(2020·浙江七年级)若方程组的解满足,则的值为(
)
A.
B.1
C.0
D.不能确定
4.(2020·江苏九年级)小明出门时身上带了100元,下表记录了他今天所有支出,其中饮料与饼干支出的金额被涂黑.若每瓶饮料5元,每包饼干8元,则小明不可能剩下多少元?( )
A.4
B.15
C.22
D.44
5.(2020·杭州育才中学九年级)某次知识竞赛共有20道题,规定:每答对一题得+5分,每答错一题得-3分,不答的题得-1分.已知欢欢这次竞赛得了72分,设欢欢答对了道题,答错了道题,则( )
A.
B.
C.
D.
6.(2020·浙江九年级专题练习)对于实数,,定义新运算,其中,为常数,等式右边为通常的加法和乘法运算,若,,则(
)
A.40
B.41
C.45
D.46
7.(2020·云南七年级期末)为确保信息安全,信息需加密传输,发送方把信息加密后发送给接收方,接收方收到信息解密后才能使用信息,加密规则为:,,加密为,,.例如:1,2,3加密后为5,7,6,当接收方收到信息6,10,16时,发送方发送的信息为(
)
A.4,1,1
B.4,6,7
C.4,1,8
D.1,6,8
8.(2020·辽宁七年级期末)《孙子算经》是中国传统数学的重要著作,其中有一道题,原文是:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根木头的长、绳子还剩余尺;将绳子对折再量木头,则木头还剩余尺,问木头长多少尺?可设木头长为尺,绳子长为尺,则所列方程组正确的是(
)
A.
B.
C.
D.
9.(2020·浙江七年级月考)已知,为常数,若方程组的解是,则方程组是解是(
)
A.
B.
C.
D.
10.(2020·石家庄市第二十七中学七年级期中)已知关于、的方程组以下结论:①当时,方程组的解也是方程的解;②存在实数,使得;③当时,;④不论取什么实数,的值始终不变,其中正确的是(
)
A.①②③
B.①②④
C.①③④
D.②③④
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020·黑龙江七年级期末)小红买了80分、120分的两种邮票,共花掉16元钱(两种邮票都买),则购买方案共有
种.
12.(2020·山东八年级期中)甲、乙两人都解方程组,甲看错a解得,乙看错b解得,正确的解是_____.
13.(2019·浙江七年级期末)如图,在大长方形中,放入六个相同的小长方形,,,则图中阴影部分面积是____.
14.(2020·长沙市南雅中学七年级月考)解方程组时,一学生把看错而得到而正确的解是那么__________.
15.(2020·广东八年级期末)方程组的解适合方程x+y=2,则k的值为_______.
16.(2020·辽宁八年级期末)已知是关于,的二元一次方程,则______.
17.(2020·重庆一中九年级)一年之计在于春,春天,是万物复苏的开始,是播种的季节,小刘准备在自家农田种植一批新鲜蔬菜,经过市场调研,他了解到,丝瓜籽每包3元,茄子籽每包4元,白菜籽1元7包,且蔬菜籽必须整包购买,小刘计划购买这三种蔬菜籽共100包(三种均有购买),经过计算,恰好需要m元.其中购买丝瓜籽的数量不少于3包且不超过6包,购买茄子籽的数量不超过19包.实际购买时,由于商家储存的蔬菜籽数量有限,小刘并末购满100包,其中购买白菜籽支付10元,购买丝瓜籽的实际数量是计划数量的两倍,购买茄子籽若干包,这样小刘实际支付比计划少12元,则小刘实际购买三种蔬菜籽共_____包.
18.(2020·湖州市第五中学七年级期中)对任意一个三位数n,如果n满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为.例如n=123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,,所以.
(1)计算:=____.(2)若s,t都是“相异数”,其中s=100x+32,t=150+y(,,x,y都是正整数),规定:,当时,求k的最小值是____.
三、解答题(本大题共7小题,共66分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020·北京七年级期末)已知关于x、y的二元一次方程y=kx+b(k、b为常数)的正整数解如表所示:
y=kx+b
x
1
2
3
y
5
3
1
求k和b的值.
20.(2020·辽宁七年级期末)解方程组(1);(2);(3)
21.(2020·遵义市播州区泮水中学九年级)对于任意实数a,b,定义关于“?”的一种运算如下:a?b=2a+b.例如3?4=2×3+4(1)求3?(﹣6)的值;(2)若x?(﹣y)=2018,且2y?x=﹣2019,求x+y的值.
22.(2020·浙江七年级期中)列二元一次方程组解应用题:某大型超市投入15000元资金购进A、B两种品牌的矿泉水共600箱,矿泉水的成本价和销售价如下表所示:(1)该大型超市购进A、B品牌矿泉水各多少箱?(2)全部销售完600箱矿泉水,该超市共获得多少利润?
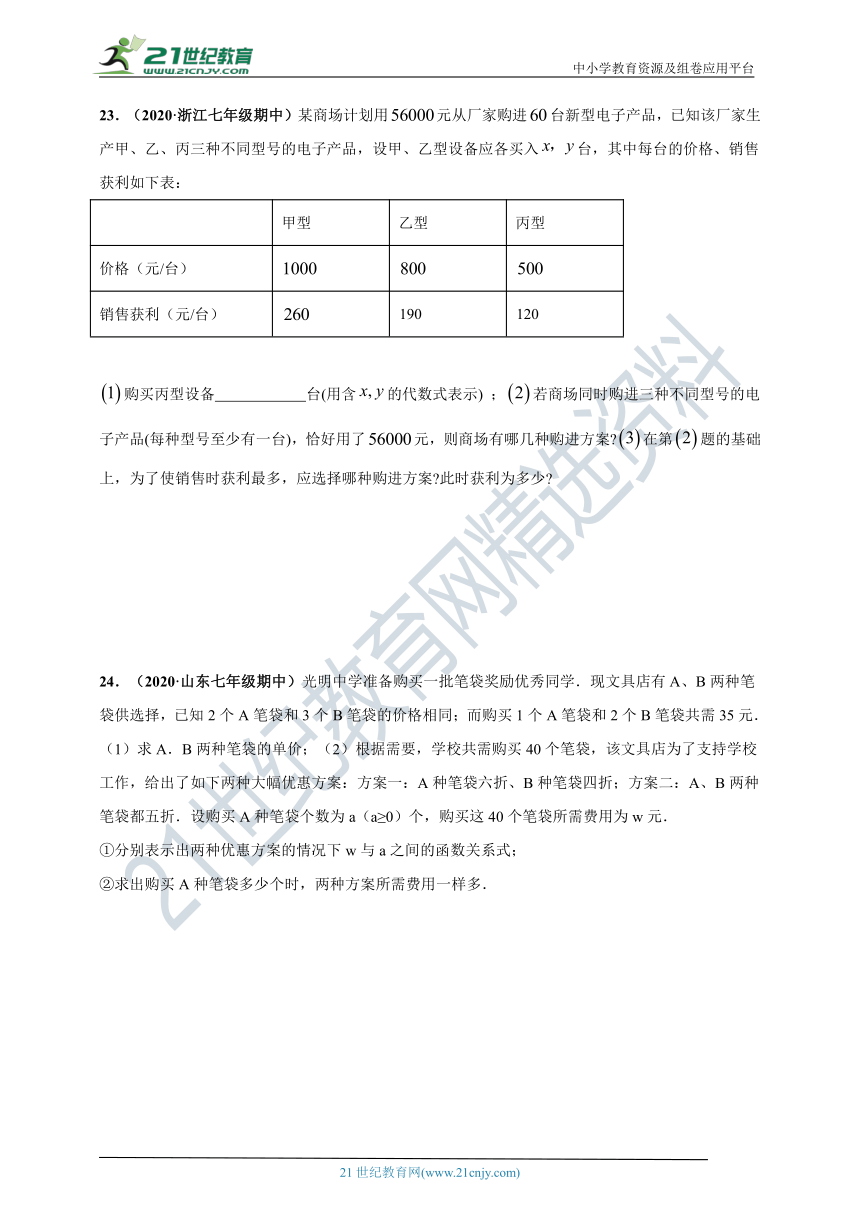
23.(2020·浙江七年级期中)某商场计划用元从厂家购进台新型电子产品,已知该厂家生产甲、乙、丙三种不同型号的电子产品,设甲、乙型设备应各买入台,其中每台的价格、销售获利如下表:
甲型
乙型
丙型
价格(元/台)
销售获利(元/台)
购买丙型设备
台(用含的代数式表示)
;若商场同时购进三种不同型号的电子产品(每种型号至少有一台),恰好用了元,则商场有哪几种购进方案?在第题的基础上,为了使销售时获利最多,应选择哪种购进方案?此时获利为多少?
24.(2020·山东七年级期中)光明中学准备购买一批笔袋奖励优秀同学.现文具店有A、B两种笔袋供选择,已知2个A笔袋和3个B笔袋的价格相同;而购买1个A笔袋和2个B笔袋共需35元.
(1)求A.B两种笔袋的单价;(2)根据需要,学校共需购买40个笔袋,该文具店为了支持学校工作,给出了如下两种大幅优惠方案:方案一:A种笔袋六折、B种笔袋四折;方案二:A、B两种笔袋都五折.设购买A种笔袋个数为a(a≥0)个,购买这40个笔袋所需费用为w元.
①分别表示出两种优惠方案的情况下w与a之间的函数关系式;
②求出购买A种笔袋多少个时,两种方案所需费用一样多.
25.(2020·山东七年级期末)某生态柑橘园现有柑橘21吨,计划租用A,B两种型号的货车将柑橘运往外地销售.已知满载时,用2辆A型车和3辆B型车一次可运柑橘12吨;用3辆A型车和4辆B型车一次可运柑橘17吨.(1)1辆A型车和1辆B型车满载时一次分别运柑橘多少吨?
(2)若计划租用A型货车m辆,B型货车n辆,一次运完全部柑橘,且每辆车均为满载.
①请帮柑橘园设计租车方案;②若A型车每辆需租金120元/次,B型车每辆需租金100元/次.请选出最省钱的租车方案,并求出最少租车费.
2020-2021学年浙教版七年级下册数学
单元测评培优卷(原版+解析版)
第2章二元一次方程
(测试时间:120分钟,满分:120分)
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020·江苏七年级月考)下列方程中,是二元一次方程的(
)
A.
B.
C.
D.
【答案】D
【分析】二元一次方程满足的条件:含有2个未知数,未知数的项的次数是1的整式方程.
【详解】A.分母含有字母,不是整式方程,故此选项不合题意;
B.
分母含有字母,不是整式方程,故此选项不合题意;
C.
分母含有字母,不是整式方程,故此选项不合题意;
D.
是二元一次方程,故此选项符合题意.故选:D.
【点睛】此题主要考查了二元一次方程的概念,要求熟悉二元一次方程的形式及其特点:含有2个未知数,未知数的项的次数是1的整式方程.
2.(2020·浙江七年级)解方程组时,①—②,得(
)
A.
.
B.
C.
D.
【答案】C
【分析】运用加减消元法求解即可.
【详解】解:解方程组时,①-②,得3t-(-6t)=2-(-1),即,9t=3,故选:C.
【点睛】此题考查解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
3.(2020·浙江七年级)若方程组的解满足,则的值为(
)
A.
B.1
C.0
D.不能确定
【答案】B
【分析】方程组中两方程相加得到以k为未知数的方程,解方程即可得答案.
【详解】解:①+②,得3(x+y)=3-3k,由x+y=0,得3-3k=0,解得k=1,故选:B.
【点睛】本题考查了二元一次方程组的解,利用等式的性质是解题关键.
4.(2020·江苏九年级)小明出门时身上带了100元,下表记录了他今天所有支出,其中饮料与饼干支出的金额被涂黑.若每瓶饮料5元,每包饼干8元,则小明不可能剩下多少元?( )
A.4
B.15
C.22
D.44
【答案】C
【分析】设买了瓶饮料,盒饼干,求出买三餐所剩的钱数,对四个选项分别讨论,得到买饮料、饼干的总钱数,列出关于二元一次方程,若这个方程有自然数解,则可能,反之,不可能.
【详解】解:设买了瓶饮料,盒饼干,为自然数,买三餐还剩100-10-15-18=57元
A.
若剩4元,则
,有整数解;
B.
若剩15元,则
,有整数解;
C.
若剩22元,则
,无整数解;
D.
若剩44元,则
,有整数解;故选:C.
【点睛】本题考查了二元一次方程的应用,解题关键是读懂题意,列出二元一次方程,把问题转化为二元一次方程的整数解的问题.
5.(2020·杭州育才中学九年级)某次知识竞赛共有20道题,规定:每答对一题得+5分,每答错一题得-3分,不答的题得-1分.已知欢欢这次竞赛得了72分,设欢欢答对了道题,答错了道题,则( )
A.
B.
C.
D.
【答案】C
【分析】设欢欢答对了道题,答错了道题,根据“每答对一题得+5分,每答错一题得-3分,不答的题得-1分,已知欢欢这次竞赛得了72分”列出方程.
【详解】解:设答对了道题,答错了道题,则不答的题有
道,
依题意得:,化简得:.故选:C.
【点睛】本题考查了由实际问题抽象出二元一次方程,关键是读懂题意,根据题目中的数量关系,列出方程,注意:本题中的等量关系之一为:答对的题目数量+答错的题目数量+不答的题目数量=20.
6.(2020·浙江九年级专题练习)对于实数,,定义新运算,其中,为常数,等式右边为通常的加法和乘法运算,若,,则(
)
A.40
B.41
C.45
D.46
【答案】B
【分析】根据定义新运算列出二元一次方程组即可求出a和b的值,再根据定义新运算公式求值即可.
【详解】解:∵,,,
∴解得:∴=41故选B.
【点睛】此题考查的是定义新运算和解二元一次方程组,掌握定义新运算公式和二元一次方程组的解法是解决此题的关键.
7.(2020·云南七年级期末)为确保信息安全,信息需加密传输,发送方把信息加密后发送给接收方,接收方收到信息解密后才能使用信息,加密规则为:,,加密为,,.例如:1,2,3加密后为5,7,6,当接收方收到信息6,10,16时,发送方发送的信息为(
)
A.4,1,1
B.4,6,7
C.4,1,8
D.1,6,8
【答案】C
【分析】由题意建立方程组,解方程组可得答案.
【详解】解:由题意得:
由③得:,把代入②得:
把代入①得:
所以:.所以发送方的信息是
故选C.
【点睛】本题考查的是新定义下的三元一次方程组,掌握解三元一次方程组是解题的关键.
8.(2020·辽宁七年级期末)《孙子算经》是中国传统数学的重要著作,其中有一道题,原文是:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根木头的长、绳子还剩余尺;将绳子对折再量木头,则木头还剩余尺,问木头长多少尺?可设木头长为尺,绳子长为尺,则所列方程组正确的是(
)
A.
B.
C.
D.
【答案】C
【分析】根据题中的等量关系即可列得方程组.
【详解】设木头长为尺,绳子长为尺,
∵用一根绳子去量一根木头的长、绳子还剩余尺,∴y=x+4.5,
∵将绳子对折再量木头,则木头还剩余尺,∴0.5y=x+1,故选:C.
【点睛】此题考查二元一次方程组的实际应用,正确理解题意找到题目中绳子和木头之间的等量关系是解题的关键.
9.(2020·浙江七年级月考)已知,为常数,若方程组的解是,则方程组是解是(
)
A.
B.
C.
D.
【答案】C
【分析】先观察两方程组的特点,由于两方程组的形式相同,故可用换元法把它们化为同一方程组,再根据方程组的解的定义,即可求解.
【详解】令x+1=X,y-2=Y,∴方程组可化为,
∵方程组的解是,∴,解得:.故选C.
【点睛】本题主要考查二元一次方程组的解的定义,掌握换元法以及方程解的定义,是解题的关键.
10.(2020·石家庄市第二十七中学七年级期中)已知关于、的方程组以下结论:①当时,方程组的解也是方程的解;②存在实数,使得;③当时,;④不论取什么实数,的值始终不变,其中正确的是(
)
A.①②③
B.①②④
C.①③④
D.②③④
【答案】B
【分析】①把k=0代入方程组求出解,代入方程检验即可;②方程组消元k得到x与y的方程,检验即可;③表示出y-x,代入已知不等式求出k的范围,判断即可;④方程组整理后表示出x+3y,检验即可.
【详解】解:①把k=0代入方程组得:,解得:,
代入方程得:左边=-2-2=-4,右边=-4,左边=右边,此选项正确;
②由x+y=0,得到y=-x,代入方程组得:,即k=3k-1,解得:,
则存在实数,使x+y=0,本选项正确;
③,解不等式组得:,
∵,∴,解得:,此选项错误;
④x+3y=3k-2+3-3k=1,本选项正确;∴正确的选项是①②④;故选:B.
【点睛】此题考查了二元一次方程组的解以及解二元一次方程组熟练掌握运算法则是解本题的关键.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020·黑龙江七年级期末)小红买了80分、120分的两种邮票,共花掉16元钱(两种邮票都买),则购买方案共有
种.
【答案】6
【分析】设80分的邮票购买x张,120分的邮票购买y张,根据题意列方程0.8x+1.2y=16,用含y的代数式表示x得,根据x、y都是整数取出x与y的对应值,得到购买方案.
【详解】解:设80分的邮票购买x张,120分的邮票购买y张,
0.8x+1.2y=16,解得,
∵x、y都是正整数,∴当y=2、4、6、8、10、12时,
x=17、14、11、8、5、2,∴共有6种购买方案,故答案为:6.
【点睛】此题考查一元二次方程的实际应用,根据题意只得到一个方程时,可将方程变形为用一个未知数表示另一个未知数的形式,然后根据未知数的要求得到对应值即可解决实际问题.
12.(2020·山东八年级期中)甲、乙两人都解方程组,甲看错a解得,乙看错b解得,正确的解是_____.
【答案】
【分析】甲看错a,但b是正确的,所以方程组的解应满足方程,把解代入可求出b的值;同理乙看错b,但a是正确的,那么把代入方程,可求a的值;把所求a、b的值代入原方程组,然后解这个方程组即可.
【详解】解:根据题意把代入得
同理,把代入方程得
把,代入得解之得故答案为:.
【点睛】本题主要考查二元一次方程组的错解复原问题.
明确虽然看错一个方程的系数,但方程的解对另一个方程而言是对的,运用这个特点,分别求出方程正确的系数,是解本题的关键所在.
13.(2019·浙江七年级期末)如图,在大长方形中,放入六个相同的小长方形,,,则图中阴影部分面积是____.
【答案】51
【分析】先设小长方形的长、宽分别为、,由题意列方程组,解得小长方形的长、宽,由可求得,再根据,可解阴影面积.
【详解】解:设小长方形的长、宽分别为、,依题意得:,
即,解得:,,,
,,,
本题的答案为51.
【点睛】本题考查了二元一次方程组的实际应用,利用了求面积中一种常用的方法割补法,面积总量不变,扣掉较容易求出的图形面积,可得解.
14.(2020·长沙市南雅中学七年级月考)解方程组时,一学生把看错而得到而正确的解是那么__________.
【答案】11
【分析】将错误的解和正确的解分别代入方程组,得出和,,联立关于的方程组,解得的值,即可得解.
【详解】将代入方程组,得①
将代入方程组,得②,
联立,得解得∴4+5+2=11故答案为:11.
【点睛】此题主要考查利用二元一次方程组的解求参数的值,熟练掌握,即可解题.
15.(2020·广东八年级期末)方程组的解适合方程x+y=2,则k的值为_______.
【答案】1
【分析】根据方程组的特点,(①+②)÷2得到x+y=k+1,组成一元一次方程求解即可.
【详解】解:(①+②)÷2得,x+y=k+1,
由题意得,k+1=2,解答,k=1,故答案为1.
【点睛】本题考查的是二元一次方程组的解,掌握加减消元法解二次一次方程组的一般步骤是解题的关键.
16.(2020·辽宁八年级期末)已知是关于,的二元一次方程,则______.
【答案】
【分析】利用二元一次方程的定义得出关于m的方程组,求出m的值即可.
【详解】∵是关于,的二元-次方程,∴,解得m=-2.
【点睛】此题主要考查了二元一次方程的定义,根据定义列出关于m的方程是解题关键,同时注意.
17.(2020·重庆一中九年级)一年之计在于春,春天,是万物复苏的开始,是播种的季节,小刘准备在自家农田种植一批新鲜蔬菜,经过市场调研,他了解到,丝瓜籽每包3元,茄子籽每包4元,白菜籽1元7包,且蔬菜籽必须整包购买,小刘计划购买这三种蔬菜籽共100包(三种均有购买),经过计算,恰好需要m元.其中购买丝瓜籽的数量不少于3包且不超过6包,购买茄子籽的数量不超过19包.实际购买时,由于商家储存的蔬菜籽数量有限,小刘并末购满100包,其中购买白菜籽支付10元,购买丝瓜籽的实际数量是计划数量的两倍,购买茄子籽若干包,这样小刘实际支付比计划少12元,则小刘实际购买三种蔬菜籽共_____包.
【答案】84.
【分析】设计划买丝瓜籽数量为a包,茄子籽b包,白菜籽c包,则3≤a≤6,0≤b≤19,c为7的倍数,且均为整数,根据题意,a+b+c=100,分情况列出所有可能的a,b,c,再分别计算出各种条件下的计划支付价格m,设实际购买丝瓜数量为x包,茄子籽y包,则实际:6≤x≤12,0≤y≤19,且x仅能为6、8、10、12(对应的a分别为3、4、5、6),进而求出符合条件的整数x和y的值,最后求出共计买的包数.
【详解】设计划买丝瓜籽数量为a包,茄子籽b包,白菜籽c包,
则3≤a≤6,0≤b≤19,c为7的倍数,且均为整数,根据题意,a+b+c=100,
分情况列出所有可能的a,b,c,具体如下:
①a=3时,b=13,c=84或b=6,c=91,②a=4时,b=12,c=84或b=5,c=91,
③a=5时,b=11,c=84或b=4,c=91,④a=6时,b=10,c=84或b=3,c=91,
再分别计算出各种条件下的计划支付价格m,设实际购买丝瓜数量为x包,茄子籽y包,则:
实际:6≤x≤12,0≤y≤19,且x仅能为6、8、10、12(对应的a分别为3、4、5、6),
∵10元买白菜籽,∴10×7=70(包),又∵实际支付比计划少12元,3x+4y+70=m﹣12,⑤
∴将x=6、8、10、12分别代入⑤式,计算得符合条件的整数y,
经计算,x=10,y=4时,符合上述所有不等式,∴共计买10+4+70=84(包).故答案为:84.
【点睛】本题考查了三元一次方程的应用,解决本题的关键是根据题意求整数解.
18.(2020·湖州市第五中学七年级期中)对任意一个三位数n,如果n满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为.例如n=123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,,所以.
(1)计算:=____.(2)若s,t都是“相异数”,其中s=100x+32,t=150+y(,,x,y都是正整数),规定:,当时,求k的最小值是____.
【答案】10
.
【分析】(1)根据“相异数”的定义列式计算即可;
(2)由s=100x+32,t=150+y结合,即可得出关于x、y的二元一次方程,解之即可得出x、y的值,再根据“相异数”的定义结合的定义式,即可求出、的值,将其代入中,即可求出最小值.
【详解】解:(1)根据“相异数”的定了可得127的三个新三位数为:217,721,172,
∴,故答案为:10;
(2)∵s,t都是“相异数”,其中s=100x+32,t=150+y,
∴,
,
∵,∴,∴,
∵,,x,y都是正整数,
∴或或或或或,
∵s是“相异数”,∴且,∵t是“相异数”,∴且,
∴或或,
①当时,,则,
②当时,,则,
③当时,,则,
∴当时,k取得最小值为,故答案为:.
【点睛】本题考查了新定义运算和二元一次方程的应用,解题的关键是根据新定义列式计算和列出关于未知数的方程.
三、解答题(本大题共7小题,共66分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020·北京七年级期末)已知关于x、y的二元一次方程y=kx+b(k、b为常数)的正整数解如表所示:
y=kx+b
x
1
2
3
y
5
3
1
求k和b的值.
【答案】k=﹣2,b=7.
【分析】根据表格把x与y对应的两对值,代入y=kx+b可得关于k、b的方程组,解方程组即可求出k与b的值.
【详解】解:把x=1,y=5;x=2,y=3代入y=kx+b,
得:,解得:,所以k=﹣2,b=7.
【点睛】本题考查了二元一次方程的解的概念和二元一次方程组的解法,属于常考题型,正确理解题意、得出相应的二元一次方程组是解题的关键.
20.(2020·辽宁七年级期末)解方程组(1);(2);(3)
【答案】(1);(2);(3)
【分析】(1)通过代入消元法,即可完成求解;(2)通过加减消元法,即可完成求解;
(3)通过加减消元法,将三元一次函数转化为二元一次方程组并求解,再将二元一次方程组的解代入三元一次方程,即可完成求解.
【详解】(1)把①代入②得:
解得y=1
把y=1代入①得:x=2
∴方程组的解为;
(2)
①+②得:
解得:
②-①得:解得:
∴方程组的解为;
(3)①-②得:x+2y=5④
②+③得:4x+2y=8⑤
⑤-④得:3x=3
解得:x=1
把x=1代入④得:y=2
把x=1,y=2代入②得:z=3
故方程组的解为:.
【点睛】本题考查了二元一次方程组和三元一次方程组的知识;解题的关键是熟练掌握代入消元法和加减消元法,从而完成对二元一次方程组和三元一次方程组的求解.
21.(2020·遵义市播州区泮水中学九年级)对于任意实数a,b,定义关于“?”的一种运算如下:a?b=2a+b.例如3?4=2×3+4(1)求3?(﹣6)的值;(2)若x?(﹣y)=2018,且2y?x=﹣2019,求x+y的值.
【答案】(1)0;(2)﹣
【分析】(1)原式利用题中的新定义计算即可求出值;
(2)已知等式利用题中的新定义化简,计算即可求出所求.
【详解】解:(1)根据题中的新定义得:原式=;
(2)已知等式利用题中的新定义得:,
化简得:,①+②得:3x+3y=﹣1,则x+y=﹣.
【点睛】此题考查了新定义下的实数运算和解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
22.(2020·浙江七年级期中)列二元一次方程组解应用题:某大型超市投入15000元资金购进A、B两种品牌的矿泉水共600箱,矿泉水的成本价和销售价如下表所示:(1)该大型超市购进A、B品牌矿泉水各多少箱?(2)全部销售完600箱矿泉水,该超市共获得多少利润?
【答案】(1)该超市进A品牌矿泉水400箱,B品牌矿泉水200箱;(2)该超市共获利润7800元
【分析】(1)设该超市进A品牌矿泉水x箱,B品牌矿泉水y箱,根据总价=单价×数量结合该超市投入15000元资金购进A、B两种品牌的矿泉水共600箱,即可得出关于x,y的二元一次方程组,解之即可得出结论;(2)根据总利润=每箱利润×数量,即可求出该超市销售万600箱矿泉水获得的利润.
【详解】解:(1)设该超市进A品牌矿泉水x箱,B品牌矿泉水y箱,
依题意,得:,
解得:.
答:该超市进A品牌矿泉水400箱,B品牌矿泉水200箱.
(2)400×(32-20)+200×(50-35)=7800(元).答:该超市共获利润7800元.
【点睛】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
23.(2020·浙江七年级期中)某商场计划用元从厂家购进台新型电子产品,已知该厂家生产甲、乙、丙三种不同型号的电子产品,设甲、乙型设备应各买入台,其中每台的价格、销售获利如下表:
甲型
乙型
丙型
价格(元/台)
销售获利(元/台)
购买丙型设备
台(用含的代数式表示)
;若商场同时购进三种不同型号的电子产品(每种型号至少有一台),恰好用了元,则商场有哪几种购进方案?在第题的基础上,为了使销售时获利最多,应选择哪种购进方案?此时获利为多少?
【答案】(1)
;
(2)
购进方案有三种,分别为:方案一:甲型台,乙型台,丙型台;方案二:甲型台,乙型台,丙型台;方案三:甲型台,乙型台,丙型台;(3)
购进甲型台,乙型台,丙型台,获利最多,为元
【分析】(1)用总台数减去甲、乙两型的数量及得丙的数量;
(2)根据总费用恰好是56000元可列写一个等式方程,其中包含2个未知数,仅能得出x、y之间的关系式:.再利用x、y都是正数,可得y必须是5的倍数;
(3)在(2)中得出的几种方案中,分别求解利润,得出利润最多的情况
【详解】解:
由题意得,
化简整理得:
当时,;当时,;
当时,.
购进方案有三种,分别为:方案一:甲型台,乙型台,丙型台;
方案二:甲型台,乙型台,丙型台;方案三:甲型台,乙型台,丙型台.
方案一:(元),故可获利元,
方案二一:(元),故可获利元,
方案三:(元),故可获利元,
因为所以购进甲型台,乙型台,丙型台,获利最多,为元.
【点睛】本题的难点是利用二元一次不定方程求解,当方程数量少于未知数时,通常是无法直接求解出未知数的值的.此刻,我们还需要根据“整数”这个条件,进行分析.
24.(2020·山东七年级期中)光明中学准备购买一批笔袋奖励优秀同学.现文具店有A、B两种笔袋供选择,已知2个A笔袋和3个B笔袋的价格相同;而购买1个A笔袋和2个B笔袋共需35元.
(1)求A.B两种笔袋的单价;(2)根据需要,学校共需购买40个笔袋,该文具店为了支持学校工作,给出了如下两种大幅优惠方案:方案一:A种笔袋六折、B种笔袋四折;方案二:A、B两种笔袋都五折.设购买A种笔袋个数为a(a≥0)个,购买这40个笔袋所需费用为w元.
①分别表示出两种优惠方案的情况下w与a之间的函数关系式;
②求出购买A种笔袋多少个时,两种方案所需费用一样多.
【答案】(1)A种笔袋的单价为15元,B种笔袋的单价为10元;(2)①方案一:;方案二:;②当购买A种笔袋16个时,两种方案所需费用一样多.
【分析】(1)根据题意,找出题目的等量关系,列出方程组,求出方程组的解,即可得到答案;
(2)①根据题意,分别列出方案一和方案二的关系式,即可得到答案;
②令两种方案的费用相等,列出方程,解方程即可得到答案.
【详解】解:(1)根据题意,设A种笔袋的单价为x元,B种笔袋的单价为y元,则
,解得:,∴A种笔袋的单价为15元,B种笔袋的单价为10元;
(2)①设购买A种笔袋个数为a(a≥0)个,则B种笔袋个数为(40-a)个,则
方案一:,∴;
方案二:,∴;
②当两种方案所需费用一样多时,有;,解得:,
∴当购买A种笔袋16个时,两种方案所需费用一样多.
【点睛】本题考查了一元一次方程的应用——方案问题,以及二元一次方程组的应用,解题的关键是正确掌握题意,正确列出方程,从而进行解题.
25.(2020·山东七年级期末)某生态柑橘园现有柑橘21吨,计划租用A,B两种型号的货车将柑橘运往外地销售.已知满载时,用2辆A型车和3辆B型车一次可运柑橘12吨;用3辆A型车和4辆B型车一次可运柑橘17吨.(1)1辆A型车和1辆B型车满载时一次分别运柑橘多少吨?
(2)若计划租用A型货车m辆,B型货车n辆,一次运完全部柑橘,且每辆车均为满载.
①请帮柑橘园设计租车方案;②若A型车每辆需租金120元/次,B型车每辆需租金100元/次.请选出最省钱的租车方案,并求出最少租车费.
【答案】(1)1辆A型车满载时一次可运柑橘3吨,1辆B型车满载时一次可运柑橘2吨;(2)①共有4种租车方案,方案1:租用1辆A型车,9辆B型车;方案2:租用3辆A型车,6辆B型车;方案3:租用5辆A型车,3辆B型车;方案4:租用7辆A型车;②最省钱的租车方案是租用7辆A型车,最少租车费是840元
【分析】(1)设1辆A型车满载时一次可运柑橘x吨,1辆B型车满载时一次可运柑橘y吨,根据“用2辆A型车和3辆B型车一次可运柑橘12吨;用3辆A型车和4辆B型车一次可运柑橘17吨”,即可得出关于x,y的二元一次方程组,解之即可得出结论;(2)①根据一次运载柑橘21吨,即可得出关于m,n的二元一次方程,结合m,n均为非负整数,即可得出各租车方案;②根据租车总费用=租用每辆车的费用×租用的辆数,即可求出各租车方案所需费用,比较后即可得出结论.
【详解】解:(1)设1辆A型车满载时一次可运柑橘x吨,1辆B型车满载时一次可运柑橘y吨,
依题意,得:,解得:.
故答案为:1辆A型车满载时一次可运柑橘3吨,1辆B型车满载时一次可运柑橘2吨.
(2)①依题意,得:3m+2n=21,∴m=7﹣n.
又∵m,n均为非负整数,∴或或或.
答:共有4种租车方案,方案1:租用1辆A型车,9辆B型车;方案2:租用3辆A型车,6辆B型车;方案3:租用5辆A型车,3辆B型车;方案4:租用7辆A型车.
②方案1所需租车费为120×1+100×9=1020(元),方案2所需租车费为120×3+100×6=960(元),
方案3所需租车费为120×5+100×3=900(元),方案4所需租车费为120×7=840(元).
∵1020>960>900>840,故答案为:最省钱的租车方案是租用7辆A型车,最少租车费是840元.
【点睛】本题主要考查列二元一次方程以及利用二元一次方程解决方案问题,正确理想二元一次方程组并运用二元一次方程解决方案问题是本题解题的关键.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
2020-2021学年浙教版七年级下册数学
单元测评培优卷(原版+解析版)
第2章二元一次方程
(测试时间:120分钟,满分:120分)
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020·江苏七年级月考)下列方程中,是二元一次方程的(
)
A.
B.
C.
D.
2.(2020·浙江七年级)解方程组时,①—②,得(
)
A.
.
B.
C.
D.
3.(2020·浙江七年级)若方程组的解满足,则的值为(
)
A.
B.1
C.0
D.不能确定
4.(2020·江苏九年级)小明出门时身上带了100元,下表记录了他今天所有支出,其中饮料与饼干支出的金额被涂黑.若每瓶饮料5元,每包饼干8元,则小明不可能剩下多少元?( )
A.4
B.15
C.22
D.44
5.(2020·杭州育才中学九年级)某次知识竞赛共有20道题,规定:每答对一题得+5分,每答错一题得-3分,不答的题得-1分.已知欢欢这次竞赛得了72分,设欢欢答对了道题,答错了道题,则( )
A.
B.
C.
D.
6.(2020·浙江九年级专题练习)对于实数,,定义新运算,其中,为常数,等式右边为通常的加法和乘法运算,若,,则(
)
A.40
B.41
C.45
D.46
7.(2020·云南七年级期末)为确保信息安全,信息需加密传输,发送方把信息加密后发送给接收方,接收方收到信息解密后才能使用信息,加密规则为:,,加密为,,.例如:1,2,3加密后为5,7,6,当接收方收到信息6,10,16时,发送方发送的信息为(
)
A.4,1,1
B.4,6,7
C.4,1,8
D.1,6,8
8.(2020·辽宁七年级期末)《孙子算经》是中国传统数学的重要著作,其中有一道题,原文是:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根木头的长、绳子还剩余尺;将绳子对折再量木头,则木头还剩余尺,问木头长多少尺?可设木头长为尺,绳子长为尺,则所列方程组正确的是(
)
A.
B.
C.
D.
9.(2020·浙江七年级月考)已知,为常数,若方程组的解是,则方程组是解是(
)
A.
B.
C.
D.
10.(2020·石家庄市第二十七中学七年级期中)已知关于、的方程组以下结论:①当时,方程组的解也是方程的解;②存在实数,使得;③当时,;④不论取什么实数,的值始终不变,其中正确的是(
)
A.①②③
B.①②④
C.①③④
D.②③④
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020·黑龙江七年级期末)小红买了80分、120分的两种邮票,共花掉16元钱(两种邮票都买),则购买方案共有
种.
12.(2020·山东八年级期中)甲、乙两人都解方程组,甲看错a解得,乙看错b解得,正确的解是_____.
13.(2019·浙江七年级期末)如图,在大长方形中,放入六个相同的小长方形,,,则图中阴影部分面积是____.
14.(2020·长沙市南雅中学七年级月考)解方程组时,一学生把看错而得到而正确的解是那么__________.
15.(2020·广东八年级期末)方程组的解适合方程x+y=2,则k的值为_______.
16.(2020·辽宁八年级期末)已知是关于,的二元一次方程,则______.
17.(2020·重庆一中九年级)一年之计在于春,春天,是万物复苏的开始,是播种的季节,小刘准备在自家农田种植一批新鲜蔬菜,经过市场调研,他了解到,丝瓜籽每包3元,茄子籽每包4元,白菜籽1元7包,且蔬菜籽必须整包购买,小刘计划购买这三种蔬菜籽共100包(三种均有购买),经过计算,恰好需要m元.其中购买丝瓜籽的数量不少于3包且不超过6包,购买茄子籽的数量不超过19包.实际购买时,由于商家储存的蔬菜籽数量有限,小刘并末购满100包,其中购买白菜籽支付10元,购买丝瓜籽的实际数量是计划数量的两倍,购买茄子籽若干包,这样小刘实际支付比计划少12元,则小刘实际购买三种蔬菜籽共_____包.
18.(2020·湖州市第五中学七年级期中)对任意一个三位数n,如果n满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为.例如n=123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,,所以.
(1)计算:=____.(2)若s,t都是“相异数”,其中s=100x+32,t=150+y(,,x,y都是正整数),规定:,当时,求k的最小值是____.
三、解答题(本大题共7小题,共66分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020·北京七年级期末)已知关于x、y的二元一次方程y=kx+b(k、b为常数)的正整数解如表所示:
y=kx+b
x
1
2
3
y
5
3
1
求k和b的值.
20.(2020·辽宁七年级期末)解方程组(1);(2);(3)
21.(2020·遵义市播州区泮水中学九年级)对于任意实数a,b,定义关于“?”的一种运算如下:a?b=2a+b.例如3?4=2×3+4(1)求3?(﹣6)的值;(2)若x?(﹣y)=2018,且2y?x=﹣2019,求x+y的值.
22.(2020·浙江七年级期中)列二元一次方程组解应用题:某大型超市投入15000元资金购进A、B两种品牌的矿泉水共600箱,矿泉水的成本价和销售价如下表所示:(1)该大型超市购进A、B品牌矿泉水各多少箱?(2)全部销售完600箱矿泉水,该超市共获得多少利润?
23.(2020·浙江七年级期中)某商场计划用元从厂家购进台新型电子产品,已知该厂家生产甲、乙、丙三种不同型号的电子产品,设甲、乙型设备应各买入台,其中每台的价格、销售获利如下表:
甲型
乙型
丙型
价格(元/台)
销售获利(元/台)
购买丙型设备
台(用含的代数式表示)
;若商场同时购进三种不同型号的电子产品(每种型号至少有一台),恰好用了元,则商场有哪几种购进方案?在第题的基础上,为了使销售时获利最多,应选择哪种购进方案?此时获利为多少?
24.(2020·山东七年级期中)光明中学准备购买一批笔袋奖励优秀同学.现文具店有A、B两种笔袋供选择,已知2个A笔袋和3个B笔袋的价格相同;而购买1个A笔袋和2个B笔袋共需35元.
(1)求A.B两种笔袋的单价;(2)根据需要,学校共需购买40个笔袋,该文具店为了支持学校工作,给出了如下两种大幅优惠方案:方案一:A种笔袋六折、B种笔袋四折;方案二:A、B两种笔袋都五折.设购买A种笔袋个数为a(a≥0)个,购买这40个笔袋所需费用为w元.
①分别表示出两种优惠方案的情况下w与a之间的函数关系式;
②求出购买A种笔袋多少个时,两种方案所需费用一样多.
25.(2020·山东七年级期末)某生态柑橘园现有柑橘21吨,计划租用A,B两种型号的货车将柑橘运往外地销售.已知满载时,用2辆A型车和3辆B型车一次可运柑橘12吨;用3辆A型车和4辆B型车一次可运柑橘17吨.(1)1辆A型车和1辆B型车满载时一次分别运柑橘多少吨?
(2)若计划租用A型货车m辆,B型货车n辆,一次运完全部柑橘,且每辆车均为满载.
①请帮柑橘园设计租车方案;②若A型车每辆需租金120元/次,B型车每辆需租金100元/次.请选出最省钱的租车方案,并求出最少租车费.
2020-2021学年浙教版七年级下册数学
单元测评培优卷(原版+解析版)
第2章二元一次方程
(测试时间:120分钟,满分:120分)
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020·江苏七年级月考)下列方程中,是二元一次方程的(
)
A.
B.
C.
D.
【答案】D
【分析】二元一次方程满足的条件:含有2个未知数,未知数的项的次数是1的整式方程.
【详解】A.分母含有字母,不是整式方程,故此选项不合题意;
B.
分母含有字母,不是整式方程,故此选项不合题意;
C.
分母含有字母,不是整式方程,故此选项不合题意;
D.
是二元一次方程,故此选项符合题意.故选:D.
【点睛】此题主要考查了二元一次方程的概念,要求熟悉二元一次方程的形式及其特点:含有2个未知数,未知数的项的次数是1的整式方程.
2.(2020·浙江七年级)解方程组时,①—②,得(
)
A.
.
B.
C.
D.
【答案】C
【分析】运用加减消元法求解即可.
【详解】解:解方程组时,①-②,得3t-(-6t)=2-(-1),即,9t=3,故选:C.
【点睛】此题考查解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
3.(2020·浙江七年级)若方程组的解满足,则的值为(
)
A.
B.1
C.0
D.不能确定
【答案】B
【分析】方程组中两方程相加得到以k为未知数的方程,解方程即可得答案.
【详解】解:①+②,得3(x+y)=3-3k,由x+y=0,得3-3k=0,解得k=1,故选:B.
【点睛】本题考查了二元一次方程组的解,利用等式的性质是解题关键.
4.(2020·江苏九年级)小明出门时身上带了100元,下表记录了他今天所有支出,其中饮料与饼干支出的金额被涂黑.若每瓶饮料5元,每包饼干8元,则小明不可能剩下多少元?( )
A.4
B.15
C.22
D.44
【答案】C
【分析】设买了瓶饮料,盒饼干,求出买三餐所剩的钱数,对四个选项分别讨论,得到买饮料、饼干的总钱数,列出关于二元一次方程,若这个方程有自然数解,则可能,反之,不可能.
【详解】解:设买了瓶饮料,盒饼干,为自然数,买三餐还剩100-10-15-18=57元
A.
若剩4元,则
,有整数解;
B.
若剩15元,则
,有整数解;
C.
若剩22元,则
,无整数解;
D.
若剩44元,则
,有整数解;故选:C.
【点睛】本题考查了二元一次方程的应用,解题关键是读懂题意,列出二元一次方程,把问题转化为二元一次方程的整数解的问题.
5.(2020·杭州育才中学九年级)某次知识竞赛共有20道题,规定:每答对一题得+5分,每答错一题得-3分,不答的题得-1分.已知欢欢这次竞赛得了72分,设欢欢答对了道题,答错了道题,则( )
A.
B.
C.
D.
【答案】C
【分析】设欢欢答对了道题,答错了道题,根据“每答对一题得+5分,每答错一题得-3分,不答的题得-1分,已知欢欢这次竞赛得了72分”列出方程.
【详解】解:设答对了道题,答错了道题,则不答的题有
道,
依题意得:,化简得:.故选:C.
【点睛】本题考查了由实际问题抽象出二元一次方程,关键是读懂题意,根据题目中的数量关系,列出方程,注意:本题中的等量关系之一为:答对的题目数量+答错的题目数量+不答的题目数量=20.
6.(2020·浙江九年级专题练习)对于实数,,定义新运算,其中,为常数,等式右边为通常的加法和乘法运算,若,,则(
)
A.40
B.41
C.45
D.46
【答案】B
【分析】根据定义新运算列出二元一次方程组即可求出a和b的值,再根据定义新运算公式求值即可.
【详解】解:∵,,,
∴解得:∴=41故选B.
【点睛】此题考查的是定义新运算和解二元一次方程组,掌握定义新运算公式和二元一次方程组的解法是解决此题的关键.
7.(2020·云南七年级期末)为确保信息安全,信息需加密传输,发送方把信息加密后发送给接收方,接收方收到信息解密后才能使用信息,加密规则为:,,加密为,,.例如:1,2,3加密后为5,7,6,当接收方收到信息6,10,16时,发送方发送的信息为(
)
A.4,1,1
B.4,6,7
C.4,1,8
D.1,6,8
【答案】C
【分析】由题意建立方程组,解方程组可得答案.
【详解】解:由题意得:
由③得:,把代入②得:
把代入①得:
所以:.所以发送方的信息是
故选C.
【点睛】本题考查的是新定义下的三元一次方程组,掌握解三元一次方程组是解题的关键.
8.(2020·辽宁七年级期末)《孙子算经》是中国传统数学的重要著作,其中有一道题,原文是:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根木头的长、绳子还剩余尺;将绳子对折再量木头,则木头还剩余尺,问木头长多少尺?可设木头长为尺,绳子长为尺,则所列方程组正确的是(
)
A.
B.
C.
D.
【答案】C
【分析】根据题中的等量关系即可列得方程组.
【详解】设木头长为尺,绳子长为尺,
∵用一根绳子去量一根木头的长、绳子还剩余尺,∴y=x+4.5,
∵将绳子对折再量木头,则木头还剩余尺,∴0.5y=x+1,故选:C.
【点睛】此题考查二元一次方程组的实际应用,正确理解题意找到题目中绳子和木头之间的等量关系是解题的关键.
9.(2020·浙江七年级月考)已知,为常数,若方程组的解是,则方程组是解是(
)
A.
B.
C.
D.
【答案】C
【分析】先观察两方程组的特点,由于两方程组的形式相同,故可用换元法把它们化为同一方程组,再根据方程组的解的定义,即可求解.
【详解】令x+1=X,y-2=Y,∴方程组可化为,
∵方程组的解是,∴,解得:.故选C.
【点睛】本题主要考查二元一次方程组的解的定义,掌握换元法以及方程解的定义,是解题的关键.
10.(2020·石家庄市第二十七中学七年级期中)已知关于、的方程组以下结论:①当时,方程组的解也是方程的解;②存在实数,使得;③当时,;④不论取什么实数,的值始终不变,其中正确的是(
)
A.①②③
B.①②④
C.①③④
D.②③④
【答案】B
【分析】①把k=0代入方程组求出解,代入方程检验即可;②方程组消元k得到x与y的方程,检验即可;③表示出y-x,代入已知不等式求出k的范围,判断即可;④方程组整理后表示出x+3y,检验即可.
【详解】解:①把k=0代入方程组得:,解得:,
代入方程得:左边=-2-2=-4,右边=-4,左边=右边,此选项正确;
②由x+y=0,得到y=-x,代入方程组得:,即k=3k-1,解得:,
则存在实数,使x+y=0,本选项正确;
③,解不等式组得:,
∵,∴,解得:,此选项错误;
④x+3y=3k-2+3-3k=1,本选项正确;∴正确的选项是①②④;故选:B.
【点睛】此题考查了二元一次方程组的解以及解二元一次方程组熟练掌握运算法则是解本题的关键.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020·黑龙江七年级期末)小红买了80分、120分的两种邮票,共花掉16元钱(两种邮票都买),则购买方案共有
种.
【答案】6
【分析】设80分的邮票购买x张,120分的邮票购买y张,根据题意列方程0.8x+1.2y=16,用含y的代数式表示x得,根据x、y都是整数取出x与y的对应值,得到购买方案.
【详解】解:设80分的邮票购买x张,120分的邮票购买y张,
0.8x+1.2y=16,解得,
∵x、y都是正整数,∴当y=2、4、6、8、10、12时,
x=17、14、11、8、5、2,∴共有6种购买方案,故答案为:6.
【点睛】此题考查一元二次方程的实际应用,根据题意只得到一个方程时,可将方程变形为用一个未知数表示另一个未知数的形式,然后根据未知数的要求得到对应值即可解决实际问题.
12.(2020·山东八年级期中)甲、乙两人都解方程组,甲看错a解得,乙看错b解得,正确的解是_____.
【答案】
【分析】甲看错a,但b是正确的,所以方程组的解应满足方程,把解代入可求出b的值;同理乙看错b,但a是正确的,那么把代入方程,可求a的值;把所求a、b的值代入原方程组,然后解这个方程组即可.
【详解】解:根据题意把代入得
同理,把代入方程得
把,代入得解之得故答案为:.
【点睛】本题主要考查二元一次方程组的错解复原问题.
明确虽然看错一个方程的系数,但方程的解对另一个方程而言是对的,运用这个特点,分别求出方程正确的系数,是解本题的关键所在.
13.(2019·浙江七年级期末)如图,在大长方形中,放入六个相同的小长方形,,,则图中阴影部分面积是____.
【答案】51
【分析】先设小长方形的长、宽分别为、,由题意列方程组,解得小长方形的长、宽,由可求得,再根据,可解阴影面积.
【详解】解:设小长方形的长、宽分别为、,依题意得:,
即,解得:,,,
,,,
本题的答案为51.
【点睛】本题考查了二元一次方程组的实际应用,利用了求面积中一种常用的方法割补法,面积总量不变,扣掉较容易求出的图形面积,可得解.
14.(2020·长沙市南雅中学七年级月考)解方程组时,一学生把看错而得到而正确的解是那么__________.
【答案】11
【分析】将错误的解和正确的解分别代入方程组,得出和,,联立关于的方程组,解得的值,即可得解.
【详解】将代入方程组,得①
将代入方程组,得②,
联立,得解得∴4+5+2=11故答案为:11.
【点睛】此题主要考查利用二元一次方程组的解求参数的值,熟练掌握,即可解题.
15.(2020·广东八年级期末)方程组的解适合方程x+y=2,则k的值为_______.
【答案】1
【分析】根据方程组的特点,(①+②)÷2得到x+y=k+1,组成一元一次方程求解即可.
【详解】解:(①+②)÷2得,x+y=k+1,
由题意得,k+1=2,解答,k=1,故答案为1.
【点睛】本题考查的是二元一次方程组的解,掌握加减消元法解二次一次方程组的一般步骤是解题的关键.
16.(2020·辽宁八年级期末)已知是关于,的二元一次方程,则______.
【答案】
【分析】利用二元一次方程的定义得出关于m的方程组,求出m的值即可.
【详解】∵是关于,的二元-次方程,∴,解得m=-2.
【点睛】此题主要考查了二元一次方程的定义,根据定义列出关于m的方程是解题关键,同时注意.
17.(2020·重庆一中九年级)一年之计在于春,春天,是万物复苏的开始,是播种的季节,小刘准备在自家农田种植一批新鲜蔬菜,经过市场调研,他了解到,丝瓜籽每包3元,茄子籽每包4元,白菜籽1元7包,且蔬菜籽必须整包购买,小刘计划购买这三种蔬菜籽共100包(三种均有购买),经过计算,恰好需要m元.其中购买丝瓜籽的数量不少于3包且不超过6包,购买茄子籽的数量不超过19包.实际购买时,由于商家储存的蔬菜籽数量有限,小刘并末购满100包,其中购买白菜籽支付10元,购买丝瓜籽的实际数量是计划数量的两倍,购买茄子籽若干包,这样小刘实际支付比计划少12元,则小刘实际购买三种蔬菜籽共_____包.
【答案】84.
【分析】设计划买丝瓜籽数量为a包,茄子籽b包,白菜籽c包,则3≤a≤6,0≤b≤19,c为7的倍数,且均为整数,根据题意,a+b+c=100,分情况列出所有可能的a,b,c,再分别计算出各种条件下的计划支付价格m,设实际购买丝瓜数量为x包,茄子籽y包,则实际:6≤x≤12,0≤y≤19,且x仅能为6、8、10、12(对应的a分别为3、4、5、6),进而求出符合条件的整数x和y的值,最后求出共计买的包数.
【详解】设计划买丝瓜籽数量为a包,茄子籽b包,白菜籽c包,
则3≤a≤6,0≤b≤19,c为7的倍数,且均为整数,根据题意,a+b+c=100,
分情况列出所有可能的a,b,c,具体如下:
①a=3时,b=13,c=84或b=6,c=91,②a=4时,b=12,c=84或b=5,c=91,
③a=5时,b=11,c=84或b=4,c=91,④a=6时,b=10,c=84或b=3,c=91,
再分别计算出各种条件下的计划支付价格m,设实际购买丝瓜数量为x包,茄子籽y包,则:
实际:6≤x≤12,0≤y≤19,且x仅能为6、8、10、12(对应的a分别为3、4、5、6),
∵10元买白菜籽,∴10×7=70(包),又∵实际支付比计划少12元,3x+4y+70=m﹣12,⑤
∴将x=6、8、10、12分别代入⑤式,计算得符合条件的整数y,
经计算,x=10,y=4时,符合上述所有不等式,∴共计买10+4+70=84(包).故答案为:84.
【点睛】本题考查了三元一次方程的应用,解决本题的关键是根据题意求整数解.
18.(2020·湖州市第五中学七年级期中)对任意一个三位数n,如果n满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为.例如n=123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,,所以.
(1)计算:=____.(2)若s,t都是“相异数”,其中s=100x+32,t=150+y(,,x,y都是正整数),规定:,当时,求k的最小值是____.
【答案】10
.
【分析】(1)根据“相异数”的定义列式计算即可;
(2)由s=100x+32,t=150+y结合,即可得出关于x、y的二元一次方程,解之即可得出x、y的值,再根据“相异数”的定义结合的定义式,即可求出、的值,将其代入中,即可求出最小值.
【详解】解:(1)根据“相异数”的定了可得127的三个新三位数为:217,721,172,
∴,故答案为:10;
(2)∵s,t都是“相异数”,其中s=100x+32,t=150+y,
∴,
,
∵,∴,∴,
∵,,x,y都是正整数,
∴或或或或或,
∵s是“相异数”,∴且,∵t是“相异数”,∴且,
∴或或,
①当时,,则,
②当时,,则,
③当时,,则,
∴当时,k取得最小值为,故答案为:.
【点睛】本题考查了新定义运算和二元一次方程的应用,解题的关键是根据新定义列式计算和列出关于未知数的方程.
三、解答题(本大题共7小题,共66分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020·北京七年级期末)已知关于x、y的二元一次方程y=kx+b(k、b为常数)的正整数解如表所示:
y=kx+b
x
1
2
3
y
5
3
1
求k和b的值.
【答案】k=﹣2,b=7.
【分析】根据表格把x与y对应的两对值,代入y=kx+b可得关于k、b的方程组,解方程组即可求出k与b的值.
【详解】解:把x=1,y=5;x=2,y=3代入y=kx+b,
得:,解得:,所以k=﹣2,b=7.
【点睛】本题考查了二元一次方程的解的概念和二元一次方程组的解法,属于常考题型,正确理解题意、得出相应的二元一次方程组是解题的关键.
20.(2020·辽宁七年级期末)解方程组(1);(2);(3)
【答案】(1);(2);(3)
【分析】(1)通过代入消元法,即可完成求解;(2)通过加减消元法,即可完成求解;
(3)通过加减消元法,将三元一次函数转化为二元一次方程组并求解,再将二元一次方程组的解代入三元一次方程,即可完成求解.
【详解】(1)把①代入②得:
解得y=1
把y=1代入①得:x=2
∴方程组的解为;
(2)
①+②得:
解得:
②-①得:解得:
∴方程组的解为;
(3)①-②得:x+2y=5④
②+③得:4x+2y=8⑤
⑤-④得:3x=3
解得:x=1
把x=1代入④得:y=2
把x=1,y=2代入②得:z=3
故方程组的解为:.
【点睛】本题考查了二元一次方程组和三元一次方程组的知识;解题的关键是熟练掌握代入消元法和加减消元法,从而完成对二元一次方程组和三元一次方程组的求解.
21.(2020·遵义市播州区泮水中学九年级)对于任意实数a,b,定义关于“?”的一种运算如下:a?b=2a+b.例如3?4=2×3+4(1)求3?(﹣6)的值;(2)若x?(﹣y)=2018,且2y?x=﹣2019,求x+y的值.
【答案】(1)0;(2)﹣
【分析】(1)原式利用题中的新定义计算即可求出值;
(2)已知等式利用题中的新定义化简,计算即可求出所求.
【详解】解:(1)根据题中的新定义得:原式=;
(2)已知等式利用题中的新定义得:,
化简得:,①+②得:3x+3y=﹣1,则x+y=﹣.
【点睛】此题考查了新定义下的实数运算和解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
22.(2020·浙江七年级期中)列二元一次方程组解应用题:某大型超市投入15000元资金购进A、B两种品牌的矿泉水共600箱,矿泉水的成本价和销售价如下表所示:(1)该大型超市购进A、B品牌矿泉水各多少箱?(2)全部销售完600箱矿泉水,该超市共获得多少利润?
【答案】(1)该超市进A品牌矿泉水400箱,B品牌矿泉水200箱;(2)该超市共获利润7800元
【分析】(1)设该超市进A品牌矿泉水x箱,B品牌矿泉水y箱,根据总价=单价×数量结合该超市投入15000元资金购进A、B两种品牌的矿泉水共600箱,即可得出关于x,y的二元一次方程组,解之即可得出结论;(2)根据总利润=每箱利润×数量,即可求出该超市销售万600箱矿泉水获得的利润.
【详解】解:(1)设该超市进A品牌矿泉水x箱,B品牌矿泉水y箱,
依题意,得:,
解得:.
答:该超市进A品牌矿泉水400箱,B品牌矿泉水200箱.
(2)400×(32-20)+200×(50-35)=7800(元).答:该超市共获利润7800元.
【点睛】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
23.(2020·浙江七年级期中)某商场计划用元从厂家购进台新型电子产品,已知该厂家生产甲、乙、丙三种不同型号的电子产品,设甲、乙型设备应各买入台,其中每台的价格、销售获利如下表:
甲型
乙型
丙型
价格(元/台)
销售获利(元/台)
购买丙型设备
台(用含的代数式表示)
;若商场同时购进三种不同型号的电子产品(每种型号至少有一台),恰好用了元,则商场有哪几种购进方案?在第题的基础上,为了使销售时获利最多,应选择哪种购进方案?此时获利为多少?
【答案】(1)
;
(2)
购进方案有三种,分别为:方案一:甲型台,乙型台,丙型台;方案二:甲型台,乙型台,丙型台;方案三:甲型台,乙型台,丙型台;(3)
购进甲型台,乙型台,丙型台,获利最多,为元
【分析】(1)用总台数减去甲、乙两型的数量及得丙的数量;
(2)根据总费用恰好是56000元可列写一个等式方程,其中包含2个未知数,仅能得出x、y之间的关系式:.再利用x、y都是正数,可得y必须是5的倍数;
(3)在(2)中得出的几种方案中,分别求解利润,得出利润最多的情况
【详解】解:
由题意得,
化简整理得:
当时,;当时,;
当时,.
购进方案有三种,分别为:方案一:甲型台,乙型台,丙型台;
方案二:甲型台,乙型台,丙型台;方案三:甲型台,乙型台,丙型台.
方案一:(元),故可获利元,
方案二一:(元),故可获利元,
方案三:(元),故可获利元,
因为所以购进甲型台,乙型台,丙型台,获利最多,为元.
【点睛】本题的难点是利用二元一次不定方程求解,当方程数量少于未知数时,通常是无法直接求解出未知数的值的.此刻,我们还需要根据“整数”这个条件,进行分析.
24.(2020·山东七年级期中)光明中学准备购买一批笔袋奖励优秀同学.现文具店有A、B两种笔袋供选择,已知2个A笔袋和3个B笔袋的价格相同;而购买1个A笔袋和2个B笔袋共需35元.
(1)求A.B两种笔袋的单价;(2)根据需要,学校共需购买40个笔袋,该文具店为了支持学校工作,给出了如下两种大幅优惠方案:方案一:A种笔袋六折、B种笔袋四折;方案二:A、B两种笔袋都五折.设购买A种笔袋个数为a(a≥0)个,购买这40个笔袋所需费用为w元.
①分别表示出两种优惠方案的情况下w与a之间的函数关系式;
②求出购买A种笔袋多少个时,两种方案所需费用一样多.
【答案】(1)A种笔袋的单价为15元,B种笔袋的单价为10元;(2)①方案一:;方案二:;②当购买A种笔袋16个时,两种方案所需费用一样多.
【分析】(1)根据题意,找出题目的等量关系,列出方程组,求出方程组的解,即可得到答案;
(2)①根据题意,分别列出方案一和方案二的关系式,即可得到答案;
②令两种方案的费用相等,列出方程,解方程即可得到答案.
【详解】解:(1)根据题意,设A种笔袋的单价为x元,B种笔袋的单价为y元,则
,解得:,∴A种笔袋的单价为15元,B种笔袋的单价为10元;
(2)①设购买A种笔袋个数为a(a≥0)个,则B种笔袋个数为(40-a)个,则
方案一:,∴;
方案二:,∴;
②当两种方案所需费用一样多时,有;,解得:,
∴当购买A种笔袋16个时,两种方案所需费用一样多.
【点睛】本题考查了一元一次方程的应用——方案问题,以及二元一次方程组的应用,解题的关键是正确掌握题意,正确列出方程,从而进行解题.
25.(2020·山东七年级期末)某生态柑橘园现有柑橘21吨,计划租用A,B两种型号的货车将柑橘运往外地销售.已知满载时,用2辆A型车和3辆B型车一次可运柑橘12吨;用3辆A型车和4辆B型车一次可运柑橘17吨.(1)1辆A型车和1辆B型车满载时一次分别运柑橘多少吨?
(2)若计划租用A型货车m辆,B型货车n辆,一次运完全部柑橘,且每辆车均为满载.
①请帮柑橘园设计租车方案;②若A型车每辆需租金120元/次,B型车每辆需租金100元/次.请选出最省钱的租车方案,并求出最少租车费.
【答案】(1)1辆A型车满载时一次可运柑橘3吨,1辆B型车满载时一次可运柑橘2吨;(2)①共有4种租车方案,方案1:租用1辆A型车,9辆B型车;方案2:租用3辆A型车,6辆B型车;方案3:租用5辆A型车,3辆B型车;方案4:租用7辆A型车;②最省钱的租车方案是租用7辆A型车,最少租车费是840元
【分析】(1)设1辆A型车满载时一次可运柑橘x吨,1辆B型车满载时一次可运柑橘y吨,根据“用2辆A型车和3辆B型车一次可运柑橘12吨;用3辆A型车和4辆B型车一次可运柑橘17吨”,即可得出关于x,y的二元一次方程组,解之即可得出结论;(2)①根据一次运载柑橘21吨,即可得出关于m,n的二元一次方程,结合m,n均为非负整数,即可得出各租车方案;②根据租车总费用=租用每辆车的费用×租用的辆数,即可求出各租车方案所需费用,比较后即可得出结论.
【详解】解:(1)设1辆A型车满载时一次可运柑橘x吨,1辆B型车满载时一次可运柑橘y吨,
依题意,得:,解得:.
故答案为:1辆A型车满载时一次可运柑橘3吨,1辆B型车满载时一次可运柑橘2吨.
(2)①依题意,得:3m+2n=21,∴m=7﹣n.
又∵m,n均为非负整数,∴或或或.
答:共有4种租车方案,方案1:租用1辆A型车,9辆B型车;方案2:租用3辆A型车,6辆B型车;方案3:租用5辆A型车,3辆B型车;方案4:租用7辆A型车.
②方案1所需租车费为120×1+100×9=1020(元),方案2所需租车费为120×3+100×6=960(元),
方案3所需租车费为120×5+100×3=900(元),方案4所需租车费为120×7=840(元).
∵1020>960>900>840,故答案为:最省钱的租车方案是租用7辆A型车,最少租车费是840元.
【点睛】本题主要考查列二元一次方程以及利用二元一次方程解决方案问题,正确理想二元一次方程组并运用二元一次方程解决方案问题是本题解题的关键.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
