2020-2021学年七年级数学浙教版下册课件1.5图形的平移 (24张)
文档属性
| 名称 | 2020-2021学年七年级数学浙教版下册课件1.5图形的平移 (24张) |  | |
| 格式 | pptx | ||
| 文件大小 | 568.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-13 19:38:07 | ||
图片预览







文档简介
1.5图形的平移
1.通过具体实例认识图形的平移。
2.了解平移的概念,理解平移的性质。
3.能按照要求作出简单的平面图形平移变换后所得的像。
教学目标
重点:平移的性质,平移图形后所得像的画法。
难点:平移图形后所得像的画法。
教学重难点
看
高楼里运转的电梯.
看
行驶的动车
看
传送带上的物品
探
A
B
A
B
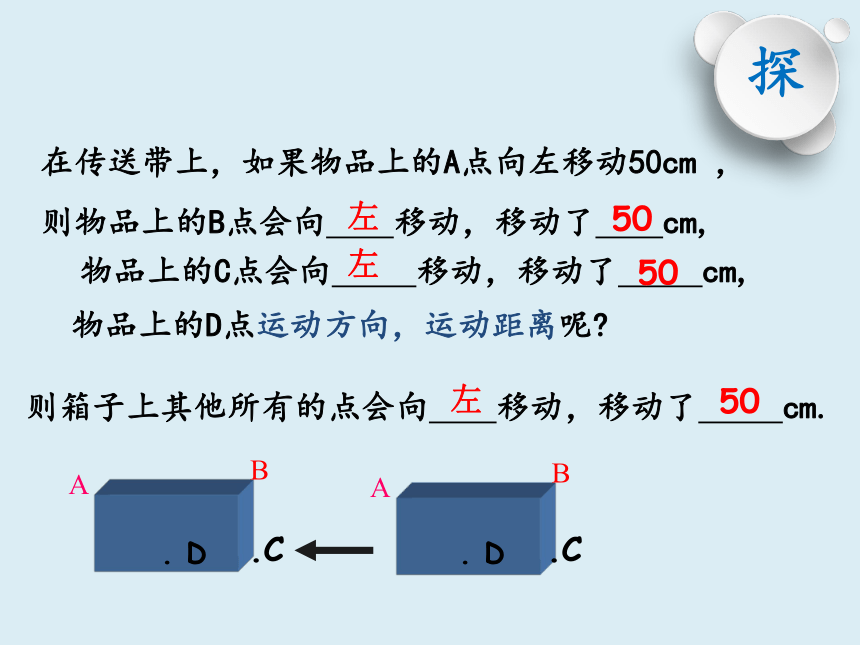
在传送带上,如果物品上的A点向左移动50cm ,
则物品上的B点会向 移动,移动了 cm,
左
50
. D
. D
.C
.C
物品上的C点会向 移动,移动了 cm,
则箱子上其他所有的点会向 移动,移动了 cm.
物品上的D点运动方向,运动距离呢?
左
50
左
50
探
问:传送带在传送物品的过程中,物品上的各点运动的方向相同吗?运动距离呢?
一个图形沿某个方向移动,在移动过程中,原图形上的所有的点都沿同一个方向移动相等的距离,这样的图形运动叫做图形的平移.
平移变换需要注意几个要点?
相同的方向,相等的距离.
忆
A
B
P
用直尺和三角板画平行线是怎么画的?
三角板发生了怎样的变化?
练
F
A
B
D
E
C
×
×
×
√
×
×
下面的运动哪些是平移,那些不是平移?
例
A
D
B
C
C?
把长方形ABCD(如图)沿箭头所指的方向平移,
使点C落在点C′.画出经这一平移后所得的像。
探
A
B
C
D
C′
1.先把透明纸覆盖在长方形ABCD上,画出相同的图形(如图2-22)
A
B
C
D
2.然后把透明约沿箭头方向平移,直到点C与点C′重合。
A′
B′
C′
D′
A
B
C
D
∴长方形A′B′C′D′就是所求平移后得到的像。
例
A
D
B
C
C?
把长方形ABCD(如图)沿箭头所指的方向平移,
使点C落在点C′.画出经这一平移后所得的像。
D ?
B ?
A ?
∴长方形A’B’C’D’就是所求
经平移后得到的像.
探
(1)找出关键点。
(2)作出这些点经平移后的点。
(3)将所作的对应点按原来方式连结,所得图形即是。
作点的平移的像是图形平移作图的基本方法.
步骤:
思
原图形与平移后所得的图形相比,哪些改变了?哪些保持不变?
连接对应点的线段之间有什么关系?
1.平移不改变图形的形状和大小.
2.一个图形和它经过平移所得的图形中,
两组对应点的连线平行(或在同一条直线上)且相等.
平移的性质:
练
C
C
C
P
下图中哪个图形可以经平移后得到图形W?请在图中
用箭头标明平移方向,并描述这个变换过程。
A
B
W
D
E
P
P′
1.分别设图形C与图形 W的两个对应顶点为P,P′。
2.将图形C沿PP′方向平移,平移的距离为线段PP′的长。
C
描述一个平移,必须指出原图形平移的方向和移动的距离。
练
如图,在三角形ABC中,BC=5 cm,将三角形ABC沿BC方向平移至三角形A′B′C′的位置时,B′恰好是BC的中点,则三角形ABC平移的距离为________cm.
2.5
结
请你说一说.
请你说一说.
概念
性质
拓
(1)图①是将线段AB向右平移1个单位长度,图②是将线段AB折一下再向右平移1个单位长度,请在图③中画出一条有两个折点的折线向右平移1个单位长度的图形;
(2)若长方形的长为a,宽为b,请分别写出(1)中三个图形中除去阴影部分后剩余部分的面积;
拓
(3)如图④,在宽为10 m,长为20 m的长方形菜地上有一条弯曲的小路,小路宽为1 m,其余部分种菜,求这块菜地种菜部分的面积.
拓
(2)剩余部分的面积均为ab-b.
(3)这块菜地种菜部分的面积为10×20-10×1=190(m2).
解:
1.作业本1.5
2.课时特训1.5
作业设计
1.通过具体实例认识图形的平移。
2.了解平移的概念,理解平移的性质。
3.能按照要求作出简单的平面图形平移变换后所得的像。
教学目标
重点:平移的性质,平移图形后所得像的画法。
难点:平移图形后所得像的画法。
教学重难点
看
高楼里运转的电梯.
看
行驶的动车
看
传送带上的物品
探
A
B
A
B
在传送带上,如果物品上的A点向左移动50cm ,
则物品上的B点会向 移动,移动了 cm,
左
50
. D
. D
.C
.C
物品上的C点会向 移动,移动了 cm,
则箱子上其他所有的点会向 移动,移动了 cm.
物品上的D点运动方向,运动距离呢?
左
50
左
50
探
问:传送带在传送物品的过程中,物品上的各点运动的方向相同吗?运动距离呢?
一个图形沿某个方向移动,在移动过程中,原图形上的所有的点都沿同一个方向移动相等的距离,这样的图形运动叫做图形的平移.
平移变换需要注意几个要点?
相同的方向,相等的距离.
忆
A
B
P
用直尺和三角板画平行线是怎么画的?
三角板发生了怎样的变化?
练
F
A
B
D
E
C
×
×
×
√
×
×
下面的运动哪些是平移,那些不是平移?
例
A
D
B
C
C?
把长方形ABCD(如图)沿箭头所指的方向平移,
使点C落在点C′.画出经这一平移后所得的像。
探
A
B
C
D
C′
1.先把透明纸覆盖在长方形ABCD上,画出相同的图形(如图2-22)
A
B
C
D
2.然后把透明约沿箭头方向平移,直到点C与点C′重合。
A′
B′
C′
D′
A
B
C
D
∴长方形A′B′C′D′就是所求平移后得到的像。
例
A
D
B
C
C?
把长方形ABCD(如图)沿箭头所指的方向平移,
使点C落在点C′.画出经这一平移后所得的像。
D ?
B ?
A ?
∴长方形A’B’C’D’就是所求
经平移后得到的像.
探
(1)找出关键点。
(2)作出这些点经平移后的点。
(3)将所作的对应点按原来方式连结,所得图形即是。
作点的平移的像是图形平移作图的基本方法.
步骤:
思
原图形与平移后所得的图形相比,哪些改变了?哪些保持不变?
连接对应点的线段之间有什么关系?
1.平移不改变图形的形状和大小.
2.一个图形和它经过平移所得的图形中,
两组对应点的连线平行(或在同一条直线上)且相等.
平移的性质:
练
C
C
C
P
下图中哪个图形可以经平移后得到图形W?请在图中
用箭头标明平移方向,并描述这个变换过程。
A
B
W
D
E
P
P′
1.分别设图形C与图形 W的两个对应顶点为P,P′。
2.将图形C沿PP′方向平移,平移的距离为线段PP′的长。
C
描述一个平移,必须指出原图形平移的方向和移动的距离。
练
如图,在三角形ABC中,BC=5 cm,将三角形ABC沿BC方向平移至三角形A′B′C′的位置时,B′恰好是BC的中点,则三角形ABC平移的距离为________cm.
2.5
结
请你说一说.
请你说一说.
概念
性质
拓
(1)图①是将线段AB向右平移1个单位长度,图②是将线段AB折一下再向右平移1个单位长度,请在图③中画出一条有两个折点的折线向右平移1个单位长度的图形;
(2)若长方形的长为a,宽为b,请分别写出(1)中三个图形中除去阴影部分后剩余部分的面积;
拓
(3)如图④,在宽为10 m,长为20 m的长方形菜地上有一条弯曲的小路,小路宽为1 m,其余部分种菜,求这块菜地种菜部分的面积.
拓
(2)剩余部分的面积均为ab-b.
(3)这块菜地种菜部分的面积为10×20-10×1=190(m2).
解:
1.作业本1.5
2.课时特训1.5
作业设计
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
