2020-2021学年七年级 数学浙教版下册课件1.4平行线的性质(2)(14张)
文档属性
| 名称 | 2020-2021学年七年级 数学浙教版下册课件1.4平行线的性质(2)(14张) |  | |
| 格式 | pptx | ||
| 文件大小 | 107.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-13 19:43:10 | ||
图片预览




文档简介
1.4平行线的性质(2)
1.掌握两条直线平行,内错角相等、同旁内角互补的性质。
2.会用平行线的性质进行推理和计算。
3.通过观察、推理、交流等活动,发展空间观念,培养实际操作能力。
教学目标
重点:平行线的性质。
难点:平行线性质的综合运用。
教学重难点
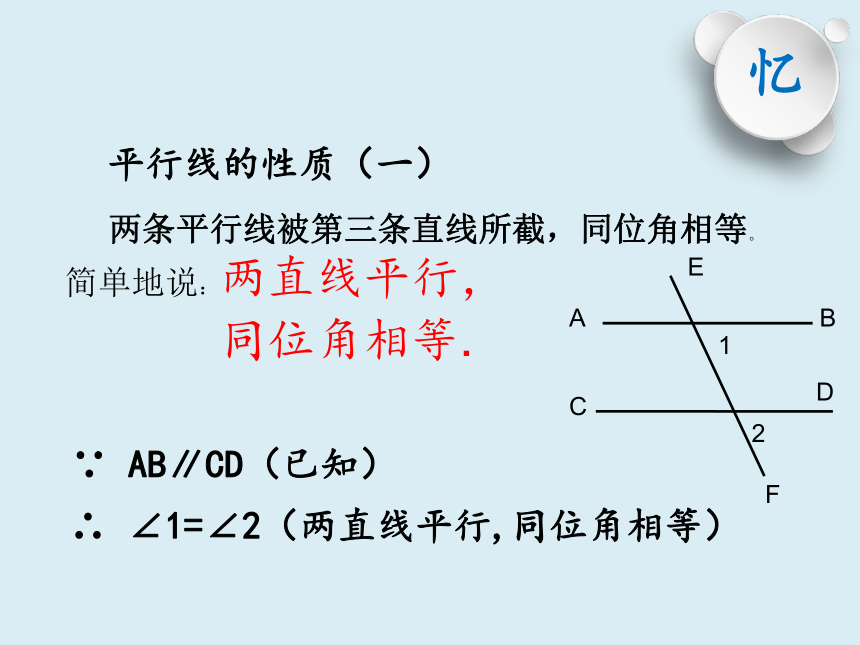
两条平行线被第三条直线所截,同位角相等。
简单地说:两直线平行,
同位角相等.
忆
∵ AB∥CD(已知)
2
1
D
A
E
B
F
C
∴ ∠1=∠2(两直线平行,同位角相等)
平行线的性质(一)
探
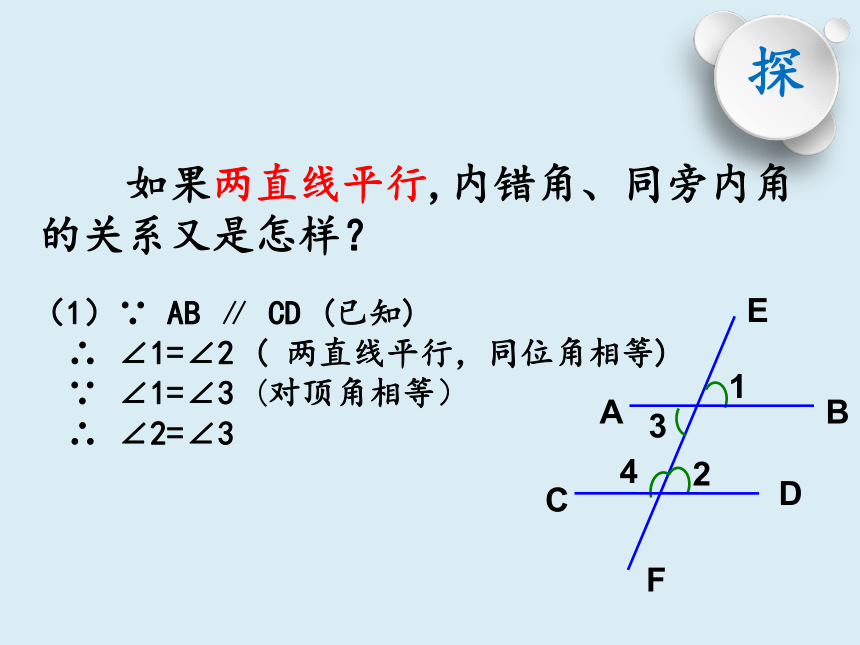
如果两直线平行,内错角、同旁内角的关系又是怎样?
(1)∵ AB ∥ CD (已知)
∴ ∠1=∠2 ( 两直线平行,同位角相等)
∵ ∠1=∠3 (对顶角相等)
∴ ∠2=∠3
4
3
2
1
F
E
D
C
B
A
探
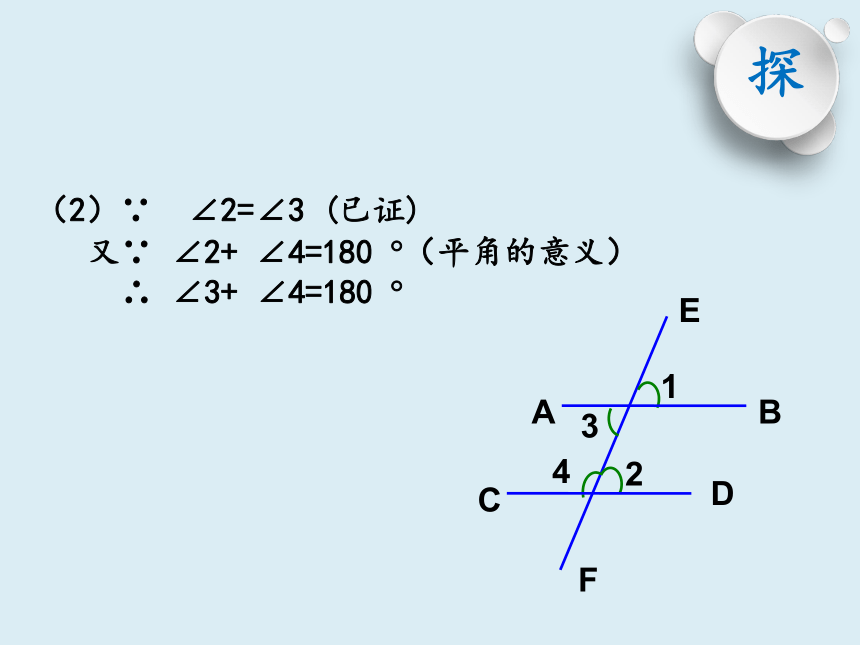
(2)∵ ∠2=∠3 (已证)
又∵ ∠2+ ∠4=180 ?(平角的意义)
∴ ∠3+ ∠4=180 ?
4
3
2
1
F
E
D
C
B
A
探
平行线的性质:
性质1:两直线平行,同位角相等.
性质3:两直线平行,同旁内角互补.
性质2:两直线平行,内错角相等.
你发现平行线还有哪些性质?
例
如图,已知AB∥CD,AD∥BC.判断∠1与∠2是否相等,并说明理由.
例
解: ∠1=∠2.理由如下:
∵AB∥CD(已知)
∴∠1+∠BAD=180°
(两直线平行,同旁内角互补)
∵AD∥BC(已知)
∴∠2+∠BAD=180°
(两直线平行,同旁内角互补),也可写成(同理)
∴∠1=∠2(同角的补角相等)
例
如图,已知∠ABC+∠C=180°,
BD平分∠ABC.∠CBD与∠D相等吗?
请说明理由。
例
解:∠CBD=∠D理由如下:
∵∠ABC+∠C=180°(已知)
∴AB∥CD
∴∠D=∠ABD
(两直线平行,内错角相等)
又∵BD平分∠ABC(已知)
∴∠CBD=∠ABD
(同旁内角互补,两直线平行)
∴∠CBD=∠D
(角平分线的定义)
(等量代换)
探
如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上,若∠1=20°,则∠2=
25°
结
请你说一说.
性质
1.作业本1.4(2)
2.课时特训1.4(2)1-12
3.自习学习1.5
作业设计
1.掌握两条直线平行,内错角相等、同旁内角互补的性质。
2.会用平行线的性质进行推理和计算。
3.通过观察、推理、交流等活动,发展空间观念,培养实际操作能力。
教学目标
重点:平行线的性质。
难点:平行线性质的综合运用。
教学重难点
两条平行线被第三条直线所截,同位角相等。
简单地说:两直线平行,
同位角相等.
忆
∵ AB∥CD(已知)
2
1
D
A
E
B
F
C
∴ ∠1=∠2(两直线平行,同位角相等)
平行线的性质(一)
探
如果两直线平行,内错角、同旁内角的关系又是怎样?
(1)∵ AB ∥ CD (已知)
∴ ∠1=∠2 ( 两直线平行,同位角相等)
∵ ∠1=∠3 (对顶角相等)
∴ ∠2=∠3
4
3
2
1
F
E
D
C
B
A
探
(2)∵ ∠2=∠3 (已证)
又∵ ∠2+ ∠4=180 ?(平角的意义)
∴ ∠3+ ∠4=180 ?
4
3
2
1
F
E
D
C
B
A
探
平行线的性质:
性质1:两直线平行,同位角相等.
性质3:两直线平行,同旁内角互补.
性质2:两直线平行,内错角相等.
你发现平行线还有哪些性质?
例
如图,已知AB∥CD,AD∥BC.判断∠1与∠2是否相等,并说明理由.
例
解: ∠1=∠2.理由如下:
∵AB∥CD(已知)
∴∠1+∠BAD=180°
(两直线平行,同旁内角互补)
∵AD∥BC(已知)
∴∠2+∠BAD=180°
(两直线平行,同旁内角互补),也可写成(同理)
∴∠1=∠2(同角的补角相等)
例
如图,已知∠ABC+∠C=180°,
BD平分∠ABC.∠CBD与∠D相等吗?
请说明理由。
例
解:∠CBD=∠D理由如下:
∵∠ABC+∠C=180°(已知)
∴AB∥CD
∴∠D=∠ABD
(两直线平行,内错角相等)
又∵BD平分∠ABC(已知)
∴∠CBD=∠ABD
(同旁内角互补,两直线平行)
∴∠CBD=∠D
(角平分线的定义)
(等量代换)
探
如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上,若∠1=20°,则∠2=
25°
结
请你说一说.
性质
1.作业本1.4(2)
2.课时特训1.4(2)1-12
3.自习学习1.5
作业设计
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
