2020-2021学年浙教版七年级下册数学课件:2.2二元一次方程组(17张)
文档属性
| 名称 | 2020-2021学年浙教版七年级下册数学课件:2.2二元一次方程组(17张) |  | |
| 格式 | pptx | ||
| 文件大小 | 157.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-16 12:21:34 | ||
图片预览





文档简介
2.2 二元一次方程组
教学目标:
1、了解二元一次方程组的概念
2、理解二元一次方程组的解的概念
3、会用列表尝试的方法求二元一次方程组的解
重点:
二元一次方程组及其解的概念
难点:
用列表尝试法求方程组的解
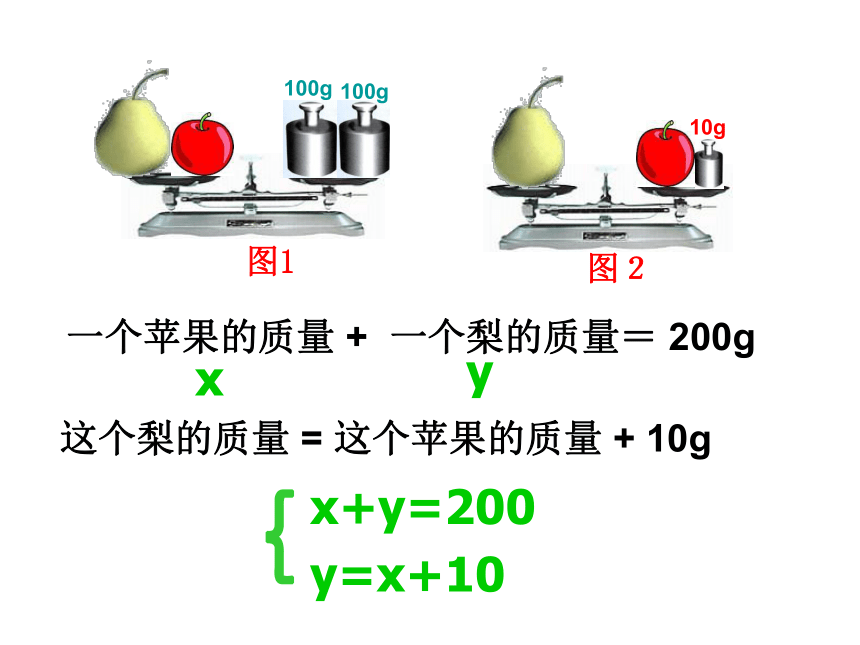
一个苹果和一个梨的质量合计200g(如图1),这个苹果的质量加上一个10g的砝码恰好与这个梨的质量相等(如图2).问苹果和梨的质量各为多少g?
100g
100g
图1
10g
图2
想一想
一个苹果的质量 + 一个梨的质量= 200g
这个梨的质量 = 这个苹果的质量 + 10g
x+y=200
y=x+10
x
y
{
100g
100g
图1
10g
图2
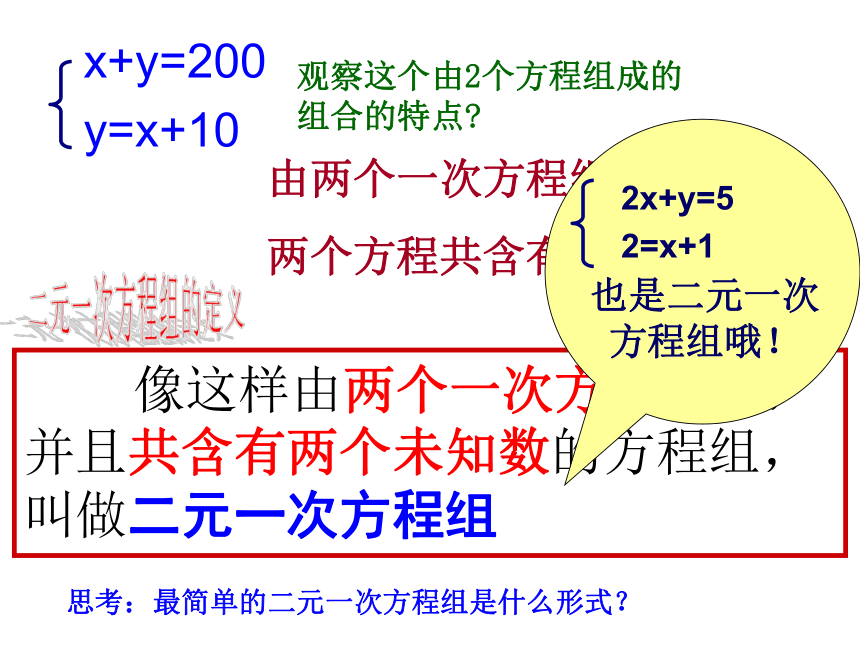
观察这个由2个方程组成的组合的特点?
由两个一次方程组成
两个方程共含有两个未知数
像这样由两个一次方程组成,并且共含有两个未知数的方程组,叫做二元一次方程组
二元一次方程组的定义
x+y=200
y=x+10
2x+y=5
2=x+1
也是二元一次方程组哦!
思考:最简单的二元一次方程组是什么形式?
1、下列方程组是二元一次方程组的是 。(填编号)
①
②
③
④
⑤
①
⑤
判断
下列各组方程组中是二元一次方程组的是( )
x+y=-5
2x=3
A
B
x=3
2x-5=6
C
D
A
做一做(课本P35)
(1)已知方程x+y=200,填写下表:
x
…
85
90
95
100
105
…
y
…
…
115
110
105
100
95
(2)已知方程y=x+10,填写下表:
x
…
85
90
95
100
105
…
y
…
…
95
100
105
110
115
问题:有没有这样的解,它既是方程x+y=200的一个解,又是
方程y=x+10的一个解?
x=95
y=105
有
同时满足二元一次方程组的各个方程的解,
叫做这个二元一次方程组的解
定义
你来试一试
把下列各组数的题序填入图中适当的位置
x=1
y=0
x=-2
y=2
方程x+y=0的解
方程2x+3y=2的解
x+y=0
2x+3y=2
方程组
的解
①
②
③
④
④
②
①
③
P83做一做2
课内练习1
例 北京2008年奥运会跳水决赛的门票价格如下表:
等级
A
B
C
票价(元/张)
500
300
150
小聪购买了B等级和C等级的跳水决赛门票共6张,他发现购买这6张门票所花的钱恰好能购买3张A等级门票。
如果设小聪购买了B等级和C等级门票分别为x张和y张,请根据问题中的条件列出关于x,y的方程组,并用列表尝试的方法求两种门票的数量
解:由题意得,
x+y=6
300x+150y=1500
因为x,y必须取自然数,所以列表尝试如下:
显然,只有x=4,y=2符合这个方程组,所以方程组的解是
x=4
y=2
答:小聪买了B等级跳水决赛门票4张,C等级跳水决赛门票2张。
x
0
1
2
3
4
5
6
y
300x+150y
6
4
5
3
2
900
1050
1350
1200
1500
找等量关系列方程
1
0
1650
1800
2.已知方程组 是二元一次方程组,求m的值
思维冲浪
构造解为 x=2 的二元一次方程组
y=-4
1.
用8块相同的长方形地砖拼成一个矩形,每个小长方形的长宽如图,请列出关于x、y的方程组,你能求出所拼成的矩形的面积吗?
思维冲浪
若方程组 2x-y=12 的解中x和y的值互为
-2x+ky=6
相反数,则k=_______,方程组的解为________
挑战题!
课堂小结
这节课你有什么收获?
作业
1、作业本2.2
2、特训2.2
3、自主学习2.3(1)
问题1:假设有一根11米长的绳子,要把它剪成两段,问每一段多少米?
如果剪成的两段长度都是正整数米,怎样剪?
如果要剪成的两段,长的一段比短的一段长3米,怎样剪?
如果要剪成的三段长度都是正整数米,且这三段首尾顺次
相接组成一个三角形,怎样剪?
x+y=11 这个二元一次方程有无穷多个解
4, 7
1, 10 ; 2 , 9 ; 3, 8; 4, 7; 5; 6 .
比比谁更聪明
5,5,1; 5,4,2; 5,3,3; 4,4,3
教学目标:
1、了解二元一次方程组的概念
2、理解二元一次方程组的解的概念
3、会用列表尝试的方法求二元一次方程组的解
重点:
二元一次方程组及其解的概念
难点:
用列表尝试法求方程组的解
一个苹果和一个梨的质量合计200g(如图1),这个苹果的质量加上一个10g的砝码恰好与这个梨的质量相等(如图2).问苹果和梨的质量各为多少g?
100g
100g
图1
10g
图2
想一想
一个苹果的质量 + 一个梨的质量= 200g
这个梨的质量 = 这个苹果的质量 + 10g
x+y=200
y=x+10
x
y
{
100g
100g
图1
10g
图2
观察这个由2个方程组成的组合的特点?
由两个一次方程组成
两个方程共含有两个未知数
像这样由两个一次方程组成,并且共含有两个未知数的方程组,叫做二元一次方程组
二元一次方程组的定义
x+y=200
y=x+10
2x+y=5
2=x+1
也是二元一次方程组哦!
思考:最简单的二元一次方程组是什么形式?
1、下列方程组是二元一次方程组的是 。(填编号)
①
②
③
④
⑤
①
⑤
判断
下列各组方程组中是二元一次方程组的是( )
x+y=-5
2x=3
A
B
x=3
2x-5=6
C
D
A
做一做(课本P35)
(1)已知方程x+y=200,填写下表:
x
…
85
90
95
100
105
…
y
…
…
115
110
105
100
95
(2)已知方程y=x+10,填写下表:
x
…
85
90
95
100
105
…
y
…
…
95
100
105
110
115
问题:有没有这样的解,它既是方程x+y=200的一个解,又是
方程y=x+10的一个解?
x=95
y=105
有
同时满足二元一次方程组的各个方程的解,
叫做这个二元一次方程组的解
定义
你来试一试
把下列各组数的题序填入图中适当的位置
x=1
y=0
x=-2
y=2
方程x+y=0的解
方程2x+3y=2的解
x+y=0
2x+3y=2
方程组
的解
①
②
③
④
④
②
①
③
P83做一做2
课内练习1
例 北京2008年奥运会跳水决赛的门票价格如下表:
等级
A
B
C
票价(元/张)
500
300
150
小聪购买了B等级和C等级的跳水决赛门票共6张,他发现购买这6张门票所花的钱恰好能购买3张A等级门票。
如果设小聪购买了B等级和C等级门票分别为x张和y张,请根据问题中的条件列出关于x,y的方程组,并用列表尝试的方法求两种门票的数量
解:由题意得,
x+y=6
300x+150y=1500
因为x,y必须取自然数,所以列表尝试如下:
显然,只有x=4,y=2符合这个方程组,所以方程组的解是
x=4
y=2
答:小聪买了B等级跳水决赛门票4张,C等级跳水决赛门票2张。
x
0
1
2
3
4
5
6
y
300x+150y
6
4
5
3
2
900
1050
1350
1200
1500
找等量关系列方程
1
0
1650
1800
2.已知方程组 是二元一次方程组,求m的值
思维冲浪
构造解为 x=2 的二元一次方程组
y=-4
1.
用8块相同的长方形地砖拼成一个矩形,每个小长方形的长宽如图,请列出关于x、y的方程组,你能求出所拼成的矩形的面积吗?
思维冲浪
若方程组 2x-y=12 的解中x和y的值互为
-2x+ky=6
相反数,则k=_______,方程组的解为________
挑战题!
课堂小结
这节课你有什么收获?
作业
1、作业本2.2
2、特训2.2
3、自主学习2.3(1)
问题1:假设有一根11米长的绳子,要把它剪成两段,问每一段多少米?
如果剪成的两段长度都是正整数米,怎样剪?
如果要剪成的两段,长的一段比短的一段长3米,怎样剪?
如果要剪成的三段长度都是正整数米,且这三段首尾顺次
相接组成一个三角形,怎样剪?
x+y=11 这个二元一次方程有无穷多个解
4, 7
1, 10 ; 2 , 9 ; 3, 8; 4, 7; 5; 6 .
比比谁更聪明
5,5,1; 5,4,2; 5,3,3; 4,4,3
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
