浙教版七下第三章《事件的可能性》整章导学案(含复习、测试)
文档属性
| 名称 | 浙教版七下第三章《事件的可能性》整章导学案(含复习、测试) |  | |
| 格式 | zip | ||
| 文件大小 | 318.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-12 19:32:19 | ||
图片预览


文档简介
3.1认识事件的可能性
预习目标
体验事件发生的可能性的意义
了解必然事件、不确定事件、不可能事件的概念,并会判断。
学会列举法(枚举、列表、画树状图)统计事件发生的 各种可能的结果数
A组(预习学案)
1.判断下列事件是必然事件,不可能事件还是不确定事件
太阳从西边升起;
抛掷一石块,石块终将落下;
在一个装着白球和黑球的袋中摸球,摸出红球;
买一张彩票,一定会中奖;
我们班所有人中,必有两个人是同月出生的。
a是实数, 则|a|≥0;
2.总结上面实例:确定事件分为:1.必然事件;2.不可能事件;3.不确定事件(随机事件)
必然事件:在一定条件下 发生的事件。
不可能事件:在一定条件下 发生的事件。
不确定事件:(随机事件)在一定条件下 发生,也可能 的事件
3.请写出必然事件,不可能事件,不确定事件各一例.然后请大家判断是否正确.
(看谁写得更精彩!)
4.探索:
在一个箱子里放有一个黑棋子和一个白棋子,它们除颜色外都相同。
(1).从箱子里摸出一个子,不放回,再摸出第二个子,这样先后摸得的两个棋子颜色有哪几种不同的可能?
(2)从箱子里摸出一个子, 放回,摇均匀后再摸出第二个子,这样先后摸得的两个棋子颜色共有哪几种不同的可能?
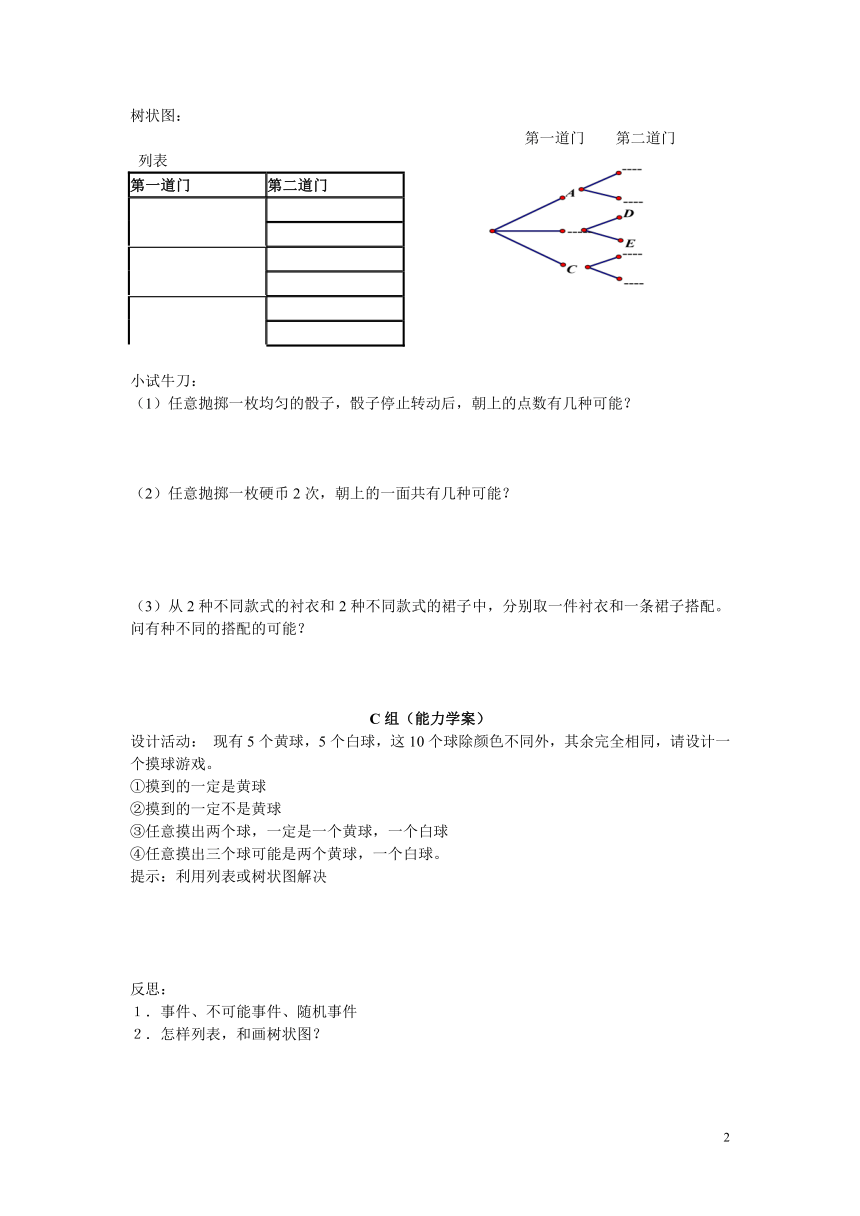
填表: 树状图:
第一次摸出一个子 第二次摸出一个子
白子
黑子
答:这样摸得的两球有4种可能: ;白,黑; ;黑,黑。
B组(课堂展示)
笼子里关着一只松鼠,笼子的主人决定把小松鼠放回大自然,将笼子所有的门都打开,松鼠要先经过第一道门(A,B或C)在经过第二道门(D或 E)才能出去,问松鼠走出笼子的路线(经过的两道门)有多少种不同的可能?
枚举法:AD,AE,BD,BE,CD,CE
树状图:
第一道门 第二道门
列表
第一道门 第二道门
小试牛刀:
(1)任意抛掷一枚均匀的骰子,骰子停止转动后,朝上的点数有几种可能?
(2)任意抛掷一枚硬币2次,朝上的一面共有几种可能?
(3)从2种不同款式的衬衣和2种不同款式的裙子中,分别取一件衬衣和一条裙子搭配。问有种不同的搭配的可能?
C组(能力学案)
设计活动: 现有5个黄球,5个白球,这10个球除颜色不同外,其余完全相同,请设计一个摸球游戏。
①摸到的一定是黄球
②摸到的一定不是黄球
③任意摸出两个球,一定是一个黄球,一个白球
④任意摸出三个球可能是两个黄球,一个白球。
提示:利用列表或树状图解决
反思:
1.事件、不可能事件、随机事件
2.怎样列表,和画树状图?
3.2可能性的大小
预习目标
认识事件发生的可能性大小的意义
2.了解事件发生的可能性的大小是由发生事件的条件来决定的
3.会在简单情境下比较事件发生的可能性的大小
A组(预习学案)
按照你的意愿,选哪个盒子呢?能说明理由吗?
1.现有三个盒子,请你从中选一个盒子任意抽取一枚围棋子,若抽到白棋,则获得奖品一份;若抽到黑棋,则送你一句祝福!
盒子1:装有1枚黑子,9枚白子
盒子2:装有8枚黑子,2枚白子
盒子3:装有5枚黑子,5枚白子
答:
2.判断一下游戏公平吗?说明你的理由。
小明和小聪一起玩掷骰子游戏,规则如下:若骰子朝上一面的数字是6,则小聪得10分;若骰子朝上一面的数字不是6,则小明得10分。谁先得到100分,谁就获胜。你认为公平吗
3.开动脑筋想想下列的情况下事件可能性的大小
(1)如果你和象棋职业棋手下一盘象棋,谁赢的可能性大?
(2)有一批成品西装,经质量检验,正品率达到98%。从这批西装中任意抽出1件,是正品的可能性大,还是次品的可能性大?
想一想:可能性的大小与什么有关
①它与可能结果的数量(所占的区域面积等)的多少有关。
数量多 可能性
数量少 可能性
②事件发生的可能性大小是由 来决定的
试一试:
1.在过十字路口时,你是否考虑过以下的问题:
某路口红绿灯的时间设置为:红灯40秒,绿灯60秒,黄灯4秒。当你随意经过该路口时,遇到哪一种灯的可能性比较大?遇到哪一种灯的可能性比较小?根据是什么?
2.游区的游览路线图如图所示.小明通过入口后,每逢路口都任选一条道.问他进入A景区或B景区的可能性哪个较大 请说明理由?
提示:利用树状图或列表先统计出总共行走的路径的可能性
B组(课堂学案)
2、小明任意买一张电影票(每排有40个座位),座位号是2的倍数与座位号是5的倍数的可能性哪个大?
3、某公交车站共有1路、12路、31路三路车停靠,已知1路车8分钟一辆;12路车5分钟一辆、31路车10分钟一辆,则在某一时刻,小明去公交车站最先等到几路车的可能性最大。
4、盒子中有8个白球、4个黄球和2个红球,除颜色外其他相同。任意摸出一个球,可能出现哪些结果?哪一种可能性最大?哪一种可能性最小?
C(能力学案)
5.某商场购物满200元,可以掷两次骰子,根据两次骰子的总点数决定送礼券多少
A
总点数 2 3 4 5 6 7 8 9 10 11 12
礼券额 20 30 40 50 60 70 80 90 100 110 120
B
总点数 2 3 4 5 6 7 8 9 10 11 12
礼券额 20 40 60 80 100 120 100 80 60 40 20
C
总点数 2 3 4 5 6 7 8 9 10 11 12
礼券额 120 100 80 60 40 20 40 60 80 100 120
如果你是商场的老总,你对促销方案有什么要求
你准备怎样去选择最佳促销方案
6.2颗小石子,游戏双方轮流拿石子,各方每次只准拿1颗或2颗.若规定一方先拿,拿到最后一颗石子者输.这个游戏公平吗
反思:
可能性的大小与什么有关
3.3可能性和概率
预习目标
1.了解概率的意义
2.了解等可能性事件的概率公式
3.会利用列举法(包括列表格、画树状图)计算简单事件发生的概率
4.进一步认识游戏规则的公平性
A组(预习学案)
1.下面是生活实际中有关可能性大小的几个例子,你能理解其中的含义吗
(1)小明可以在一 分时间内打字50个以上,那么即小明在一分时间内打字50个的可能性是100%.
(2)小华 秒内跑完100米, 即小华在7秒内跑完100米的可能性是0
(3)通过随机摇奖,要把 份奖品奖给10个人中的一个,每人得奖的可能性是1/10
一个箱子里有3个红球,1个白球(除颜色外其它都相同),小明从中任意摸一球是红球的可能性有多大
3.记忆的概念
(1)在数学上,我们把事件发生的可能性的大小也称为事件发生的
(2)表示摸到红球的可能性,也叫做摸到红球的概率(probability)。概率用英文probability的第一个字母p来表示
注意:公式在等可能性下适用
你能写出摸到白球的概率吗?
解:P(摸到白球)=
若把摸球游戏换成4个黄球, 那么摸到黄球、白球的概率分别是多少?
解:P(摸到黄球)=
P(摸到白球)=
想一想:
你知道必然事件的概率与不可能事件的概率吗?
P(必然事件)=
P(不可能事件)=
你能说出不确定事件A的概率的范围吗?
<P(A)<
4.试一试
抛掷一枚均匀的骰子,当骰子停止转动后,朝上一面的数是偶数的概率是多少?是正数的概率是多少?是负数的概率是多少?
B组(课堂学案)
5.在我们班中任意抽取1人做游 戏,你被抽到的概率是多少?
6.一副扑克牌(去掉大、小王),
任意抽取其中一张,抽到方块的概率是多少?抽到黑桃的概率呢?
7.一个红、黄两色各占一半的转盘,让转盘自由转动2次,指针2次都指向红色区域的概率是多少?一次指向红色,另一次指向黄色区域的概率是多少?
8.连续两次抛掷一枚均匀的硬 币,均正面朝上的概率是_____;
9.一个布袋里装有7个白球和3个红球,它们除颜色外其它都相同.从中任意摸一球是红球的概率是______;
10.从你所在的小组任意挑选一名同学到讲台前展示,正好挑中你的可能性是多少?
C组(能力学案)
有5张数字卡片,它们的背面完全相同,正面分别标有1,2,2,3,4。现将它们的背面朝上,从中任意摸到一张卡片,则
(1)摸到1号卡片、2号卡片、 3号卡片、 4号卡片的概率分别是多少?
(2)摸到是奇数的卡片的概率和摸到是偶数的卡片的概率分别是多少?
(3)若有一名同学摸过一张后,不吧摸到的卡片放回,另一名同学摸到2号卡片的概率是该怎么计算?
反思:(1)
(2)三种事件发生的概率及表示
①必然事件发生的概率为 ,记作 ;
②不可能事件发生的概率为 ,记作 ;
③若A为不确定事件,则 <P(A)< , 适用条件 ,
计算公式 :P(A)=
PAGE
5
预习目标
体验事件发生的可能性的意义
了解必然事件、不确定事件、不可能事件的概念,并会判断。
学会列举法(枚举、列表、画树状图)统计事件发生的 各种可能的结果数
A组(预习学案)
1.判断下列事件是必然事件,不可能事件还是不确定事件
太阳从西边升起;
抛掷一石块,石块终将落下;
在一个装着白球和黑球的袋中摸球,摸出红球;
买一张彩票,一定会中奖;
我们班所有人中,必有两个人是同月出生的。
a是实数, 则|a|≥0;
2.总结上面实例:确定事件分为:1.必然事件;2.不可能事件;3.不确定事件(随机事件)
必然事件:在一定条件下 发生的事件。
不可能事件:在一定条件下 发生的事件。
不确定事件:(随机事件)在一定条件下 发生,也可能 的事件
3.请写出必然事件,不可能事件,不确定事件各一例.然后请大家判断是否正确.
(看谁写得更精彩!)
4.探索:
在一个箱子里放有一个黑棋子和一个白棋子,它们除颜色外都相同。
(1).从箱子里摸出一个子,不放回,再摸出第二个子,这样先后摸得的两个棋子颜色有哪几种不同的可能?
(2)从箱子里摸出一个子, 放回,摇均匀后再摸出第二个子,这样先后摸得的两个棋子颜色共有哪几种不同的可能?
填表: 树状图:
第一次摸出一个子 第二次摸出一个子
白子
黑子
答:这样摸得的两球有4种可能: ;白,黑; ;黑,黑。
B组(课堂展示)
笼子里关着一只松鼠,笼子的主人决定把小松鼠放回大自然,将笼子所有的门都打开,松鼠要先经过第一道门(A,B或C)在经过第二道门(D或 E)才能出去,问松鼠走出笼子的路线(经过的两道门)有多少种不同的可能?
枚举法:AD,AE,BD,BE,CD,CE
树状图:
第一道门 第二道门
列表
第一道门 第二道门
小试牛刀:
(1)任意抛掷一枚均匀的骰子,骰子停止转动后,朝上的点数有几种可能?
(2)任意抛掷一枚硬币2次,朝上的一面共有几种可能?
(3)从2种不同款式的衬衣和2种不同款式的裙子中,分别取一件衬衣和一条裙子搭配。问有种不同的搭配的可能?
C组(能力学案)
设计活动: 现有5个黄球,5个白球,这10个球除颜色不同外,其余完全相同,请设计一个摸球游戏。
①摸到的一定是黄球
②摸到的一定不是黄球
③任意摸出两个球,一定是一个黄球,一个白球
④任意摸出三个球可能是两个黄球,一个白球。
提示:利用列表或树状图解决
反思:
1.事件、不可能事件、随机事件
2.怎样列表,和画树状图?
3.2可能性的大小
预习目标
认识事件发生的可能性大小的意义
2.了解事件发生的可能性的大小是由发生事件的条件来决定的
3.会在简单情境下比较事件发生的可能性的大小
A组(预习学案)
按照你的意愿,选哪个盒子呢?能说明理由吗?
1.现有三个盒子,请你从中选一个盒子任意抽取一枚围棋子,若抽到白棋,则获得奖品一份;若抽到黑棋,则送你一句祝福!
盒子1:装有1枚黑子,9枚白子
盒子2:装有8枚黑子,2枚白子
盒子3:装有5枚黑子,5枚白子
答:
2.判断一下游戏公平吗?说明你的理由。
小明和小聪一起玩掷骰子游戏,规则如下:若骰子朝上一面的数字是6,则小聪得10分;若骰子朝上一面的数字不是6,则小明得10分。谁先得到100分,谁就获胜。你认为公平吗
3.开动脑筋想想下列的情况下事件可能性的大小
(1)如果你和象棋职业棋手下一盘象棋,谁赢的可能性大?
(2)有一批成品西装,经质量检验,正品率达到98%。从这批西装中任意抽出1件,是正品的可能性大,还是次品的可能性大?
想一想:可能性的大小与什么有关
①它与可能结果的数量(所占的区域面积等)的多少有关。
数量多 可能性
数量少 可能性
②事件发生的可能性大小是由 来决定的
试一试:
1.在过十字路口时,你是否考虑过以下的问题:
某路口红绿灯的时间设置为:红灯40秒,绿灯60秒,黄灯4秒。当你随意经过该路口时,遇到哪一种灯的可能性比较大?遇到哪一种灯的可能性比较小?根据是什么?
2.游区的游览路线图如图所示.小明通过入口后,每逢路口都任选一条道.问他进入A景区或B景区的可能性哪个较大 请说明理由?
提示:利用树状图或列表先统计出总共行走的路径的可能性
B组(课堂学案)
2、小明任意买一张电影票(每排有40个座位),座位号是2的倍数与座位号是5的倍数的可能性哪个大?
3、某公交车站共有1路、12路、31路三路车停靠,已知1路车8分钟一辆;12路车5分钟一辆、31路车10分钟一辆,则在某一时刻,小明去公交车站最先等到几路车的可能性最大。
4、盒子中有8个白球、4个黄球和2个红球,除颜色外其他相同。任意摸出一个球,可能出现哪些结果?哪一种可能性最大?哪一种可能性最小?
C(能力学案)
5.某商场购物满200元,可以掷两次骰子,根据两次骰子的总点数决定送礼券多少
A
总点数 2 3 4 5 6 7 8 9 10 11 12
礼券额 20 30 40 50 60 70 80 90 100 110 120
B
总点数 2 3 4 5 6 7 8 9 10 11 12
礼券额 20 40 60 80 100 120 100 80 60 40 20
C
总点数 2 3 4 5 6 7 8 9 10 11 12
礼券额 120 100 80 60 40 20 40 60 80 100 120
如果你是商场的老总,你对促销方案有什么要求
你准备怎样去选择最佳促销方案
6.2颗小石子,游戏双方轮流拿石子,各方每次只准拿1颗或2颗.若规定一方先拿,拿到最后一颗石子者输.这个游戏公平吗
反思:
可能性的大小与什么有关
3.3可能性和概率
预习目标
1.了解概率的意义
2.了解等可能性事件的概率公式
3.会利用列举法(包括列表格、画树状图)计算简单事件发生的概率
4.进一步认识游戏规则的公平性
A组(预习学案)
1.下面是生活实际中有关可能性大小的几个例子,你能理解其中的含义吗
(1)小明可以在一 分时间内打字50个以上,那么即小明在一分时间内打字50个的可能性是100%.
(2)小华 秒内跑完100米, 即小华在7秒内跑完100米的可能性是0
(3)通过随机摇奖,要把 份奖品奖给10个人中的一个,每人得奖的可能性是1/10
一个箱子里有3个红球,1个白球(除颜色外其它都相同),小明从中任意摸一球是红球的可能性有多大
3.记忆的概念
(1)在数学上,我们把事件发生的可能性的大小也称为事件发生的
(2)表示摸到红球的可能性,也叫做摸到红球的概率(probability)。概率用英文probability的第一个字母p来表示
注意:公式在等可能性下适用
你能写出摸到白球的概率吗?
解:P(摸到白球)=
若把摸球游戏换成4个黄球, 那么摸到黄球、白球的概率分别是多少?
解:P(摸到黄球)=
P(摸到白球)=
想一想:
你知道必然事件的概率与不可能事件的概率吗?
P(必然事件)=
P(不可能事件)=
你能说出不确定事件A的概率的范围吗?
<P(A)<
4.试一试
抛掷一枚均匀的骰子,当骰子停止转动后,朝上一面的数是偶数的概率是多少?是正数的概率是多少?是负数的概率是多少?
B组(课堂学案)
5.在我们班中任意抽取1人做游 戏,你被抽到的概率是多少?
6.一副扑克牌(去掉大、小王),
任意抽取其中一张,抽到方块的概率是多少?抽到黑桃的概率呢?
7.一个红、黄两色各占一半的转盘,让转盘自由转动2次,指针2次都指向红色区域的概率是多少?一次指向红色,另一次指向黄色区域的概率是多少?
8.连续两次抛掷一枚均匀的硬 币,均正面朝上的概率是_____;
9.一个布袋里装有7个白球和3个红球,它们除颜色外其它都相同.从中任意摸一球是红球的概率是______;
10.从你所在的小组任意挑选一名同学到讲台前展示,正好挑中你的可能性是多少?
C组(能力学案)
有5张数字卡片,它们的背面完全相同,正面分别标有1,2,2,3,4。现将它们的背面朝上,从中任意摸到一张卡片,则
(1)摸到1号卡片、2号卡片、 3号卡片、 4号卡片的概率分别是多少?
(2)摸到是奇数的卡片的概率和摸到是偶数的卡片的概率分别是多少?
(3)若有一名同学摸过一张后,不吧摸到的卡片放回,另一名同学摸到2号卡片的概率是该怎么计算?
反思:(1)
(2)三种事件发生的概率及表示
①必然事件发生的概率为 ,记作 ;
②不可能事件发生的概率为 ,记作 ;
③若A为不确定事件,则 <P(A)< , 适用条件 ,
计算公式 :P(A)=
PAGE
5
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
