2020-2021学年七年级数学浙教版下册第2章二元一次方程组期中复习培优训练(附答案)
文档属性
| 名称 | 2020-2021学年七年级数学浙教版下册第2章二元一次方程组期中复习培优训练(附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 163.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-12 23:22:42 | ||
图片预览




文档简介
2020-2021年度浙教版七年级数学下册第2章二元一次方程组期中复习培优训练(附答案)
1.若|x﹣y﹣1|+3(x+y)2=0,则x、y的值为( )
A.x=0.5,y=0.5
B.x=﹣0.5,y=﹣0.5
C.x=﹣0.5,y=0.5
D.x=0.5,y=﹣0.5
2.一个两位数加18所得的数是它的个位数字与十位数字换了位置后的数,则这个两位数是( )A.13
B.13或14
C.有9种可能
D.有7种可能
3.两个缸内共有48桶水,甲缸给乙缸加水一倍,然后乙缸又给甲缸加甲缸剩余水的一倍,则两缸水量相等同,问最初两缸内各有水( )桶.
A.30桶,16桶
B.15桶,18桶
C.30桶,18桶
D.30桶,12桶
4.若关于x,y的方程组没有实数解,则( )
A.ab=﹣2
B.ab=﹣2且a≠1
C.ab≠﹣2
D.ab=﹣2且a≠2
5.如果,则2x:3y等于( )
A.﹣2
B.
C.2
D.
6.已知实数x、y、z满足3x+7y+z=5,4x+10y+z=3,则x+y+z=( )
A.9
B.10
C.12
D.不确定
7.方程x+2y=7在自然数范围内的解( )
A.有无数个
B.只有一个
C.只有3个
D.以上都不对
8.如果一个三角形的三边a
b
c满足关系式+|a﹣b+2|+(c﹣10)2=0,那么这个三角形的形状为( )
A.锐角三角形
B.钝角三角形
C.直角三角形
D.以上都不对
9.有铅笔、练习本、圆珠笔三种学习用品,若购铅笔3支,练习本7本,圆珠笔1支共需3.15元;若购铅笔4支,练习本8本,圆珠笔2支共需4.2元,那么,购铅笔、练习本、圆珠笔各1件共需( )
A.1.2元
B.1.05元
C.0.95元
D.0.9元
10.若x=时,关于x,y的二元一次方程组的解x,y互为倒数,则a﹣2b=
.
11.如果1台大收割机和1台小收割机每小时各收割小麦x公顷和y公顷,那么2台大收割机和5台小收割机1小时收割小麦
公顷,3台大收割机和2台小收割机1小时收割小麦
公顷.
12.已知方程组中,x,y的值相等,则n=
.
13.若的解是方程ax﹣3y=2的一组解,则a的值是
.
14.某长方形的周长是44,若宽的3倍比长多6,则该长方形的长等于
.
15.寒假期间,爱学习的小明决定将部分压岁钱用于购买A、B两种文具,2月10日,A文具的单价比B文具的单价少2元,小明购进A、B两种文具共3件;2月20日,A文具的单价翻倍,B文具的单价不变,小明购进A、B两种文具共4件.若A、B文具的单价和数量均为正整数且小明第二次购买文具比第一次购买文具多花费5元,则小明两次购买文具共花费
元.
16.(黑龙江)写出满足方程x+2y=9的一对整数解
.
17.打折前,买50件A商品和30件B商品用了920元,买60件A商品和10件B产品用了1000元.打折后,买400件A商品和400件B商品用了7500元,比不打折时少花的钱数为
元.
18.若方程x﹣y=﹣1的一个解与方程组的解相同,则k的值为
.
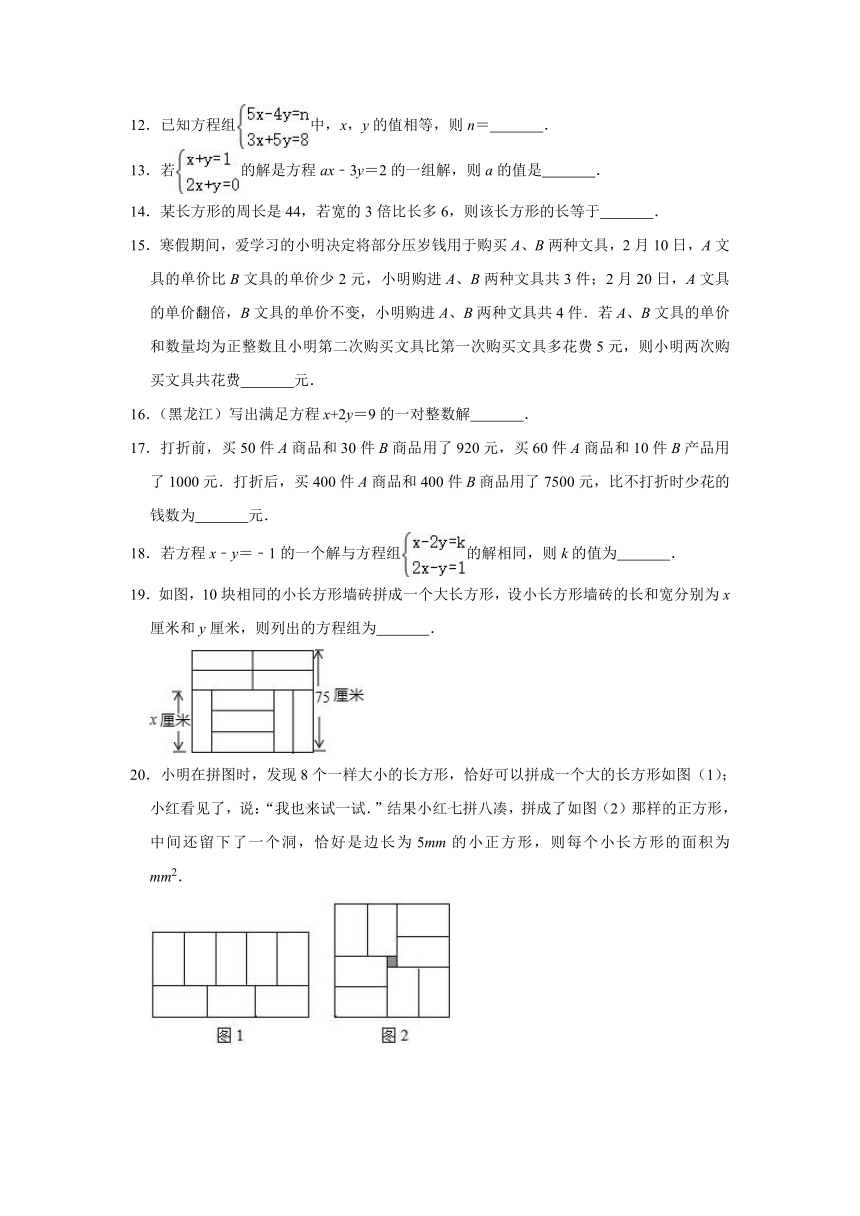
19.如图,10块相同的小长方形墙砖拼成一个大长方形,设小长方形墙砖的长和宽分别为x厘米和y厘米,则列出的方程组为
.
20.小明在拼图时,发现8个一样大小的长方形,恰好可以拼成一个大的长方形如图(1);小红看见了,说:“我也来试一试.”结果小红七拼八凑,拼成了如图(2)那样的正方形,中间还留下了一个洞,恰好是边长为5mm的小正方形,则每个小长方形的面积为
mm2.
21.已知关于x,y的方程组
(1)请直接写出方程x+2y﹣6=0的所有正整数解;
(2)若方程组的解满足x+y=0,求m的值;
(3)无论实数m取何值,方程x﹣2y+mx+5=0总有一个固定的解,请直接写出这个解?
22.已知关于x,y的二元一次方程组的解满足方程x﹣2y+1=0,求m的值.
23.某校“数学建模”社团的同学用五个正方形拼成如图所示的无缝隙、不重叠的长方形,若中间小正方形的边长为1,求正方形a和b的边长.
24.已知关于x,y的方程组与的解相同,求mn的值.
25.阅读材料:善于思考的小明在解方程组时,采用了一种“整体代换”的解法,解法如下:
解:将方程②8x+20y+2y=10,变形为2(4x+10y)+2y=10③,把方程①代入③得,2×6+2y=10,则y=﹣1;把y=﹣1代入①得,x=4,所以方程组的解为:
请你解决以下问题:
(1)试用小明的“整体代换”的方法解方程组
(2)已知x、y、z,满足试求z的值.
26.平价商场经销的甲,乙两种商品,甲种商品每件售价98元,利润率为40%;乙种商品每件进价80元,售价128元.
(1)求甲种商品每件的进价;(利润率=×100%)
(2)若该商场同时购进甲、乙两种商品共50件,恰好总进价为3800元,求购进甲、乙两种商品各多少件?
(3)在“元旦”期间,该商场只对乙种商品进行如表的优惠促销活动:
打折前一次性购物总金额
优惠措施
少于等于480元
不优惠
超过480元,但不超过680元
其中480元不打折,超过480元的部分给予6折优惠
超过680元
按购物总额给予7.5折优惠
按表的优惠条件,若小华一次性购买乙种商品实际付款576元,求小华在该商场购买乙种商品多少件?
27.问题:有甲、乙、丙三种商品,①购甲3件、乙5件、丙7件共需490元钱;②购甲4件、乙7件、丙10件共需690元钱;③购甲2件,乙3件,丙1件共需170元钱.求购甲、乙、丙三种商品各一件共需多少元?
小明说:“可以根据3个条件列出三元一次方程组,分别求出购甲、乙、丙一件需多少钱,再相加即可求得答案.”
小丽经过一番思考后,说:“本题可以去掉条件③,只用①②两个条件,仍能求出答案.”针对小丽的发言,同学们进行了热烈地讨论.
(1)请你按小明的思路解决问题.
(2)小丽的说法正确吗?如果正确,请完成解答过程;如果不正确,请说明理由.
(3)请根据上述解决问题中积累的经验,解决下面的问题:学校购买四种教学用具A、B、C、D,第一次购A教具1件、B教具3件、C教具4件、D教具5件共花2018元;第二次购A教具1件、B教具5件、C教具7件、D教具9件共花3036元.求购A教具5件、B教具3件、C教具2件、D教具1件共需多少元?
参考答案
1.解:依题意得:,
由(1)得:x=y+1…(3),
将(3)代入(2)中得:y+1+y=2y+1=0,
y=﹣0.5…(4).
将(4)代入(3)得:x=0.5.
故选:D.
2.解:设原两位数的十位数字为a,个位数字为b,
则10a+b+18=10b+a,
∴b﹣a=2,
∴b=a+2.
a可取1,2,3,4,5,6,7,
故有7种可能.
故选:D.
3.解:设甲有x桶,乙有y桶,
,
.
甲缸内有水30桶,乙缸有水18桶.
故选:C.
4.解:,
由①得,x=﹣1﹣ay,
代入②得,b(﹣1﹣ay)﹣2y+a=0,
即(﹣ab﹣2)y=b﹣a,
因为此方程组没有实数根,所以﹣ab﹣2=0,ab=﹣2.
故选:A.
5.解:在中,
①×4﹣②,得3x=9,
x=3.
代入①,得y=1.
∴2x:3y=2×3:3×1=2.
故选:C.
6.解:由x、y、z满足3x+7y+z=5和4x+10y+z=3,
得出:,
解得:,
故选:A.
7.解:由已知,得y=,
要使x,y都是自然数,
合适的x值只能是x=1,3,5,7,
相应的y值为y=3,2,1,0.
∴解为,,,.
故选:D.
8.解:∵+|a﹣b+2|+(c﹣10)2=0
∴,
解得:,
则这个三角形的形状为直角三角形,
故选:C.
9.解:设购一支铅笔,一本练习本,一支圆珠笔分别需要x,y,z元,
根据题意得,
②﹣①得x+y+z=1.05(元).
故选:B.
10.解:由于x、y互为倒数,x=,则y=2,
代入二元一次方程组,
得,
解得a=10,b=﹣,
则a﹣2b=11.
故本题答案为:11.
11.解:由于1台大收割机和1台小收割机1小时各收割小麦x公顷和y公顷.
根据题意得么2台大收割机和5台小收割机1小时收割小麦
(2x+5y)公顷,3台大收割机和2台小收割机1小时收割小麦(3x+2y)公顷.
故答案为(2x+5y),(3x+2y).
12.解:由解得,
∴5x﹣4y=5﹣4=1.
故答案为1.
13.解:解方程组得:,
把代入方程ax﹣3y=2得:﹣a﹣6=2,
解得:a=﹣8,
故答案为:﹣8.
14.解:设长方形的长为x,宽为y.
则,
解得.
则该长方形的长等于15.
故填15.
15.解:设B文具的单价为x元/件,第一次购买文具共花费y元,
依题意,得:
①当第一次买A文具1个,第二次买A文具1个,
,
解得:,不合题意舍去.
②当第一次买A文具1个,第二次买A文具2个,
,
解得:,不合题意舍去.
③当第一次买A文具1个,第二次买A文具3个
,
解得:,不合题意舍去.
④当第一次买A文具2个,第二次买A文具1个
,
解得:,不合题意舍去.
⑤当第一次买A文具2个,第二次买A文具2个
,
解得:,符合题意.
⑥当第一次买A文具2个,第二次买A文具3个
,
解得,不合题意舍去.
∴x=3,y=5,
∴y+y+5=15.
故答案为:15.
16.解:假设y=1,
把y=1代入方程得:x=7,
∴是方程x+2y=9的一对整数解.
17.解:设打折前A商品每件x元,B商品每件y元,根据题意得:
,
解得:,
则打折前买400件A商品和400件B商品需要400×16+400×4=8000(元),
则打折后比打折前少花8000﹣7500=500(元).
故答案为:500.
18.解:联立得:,
解得:,
代入方程得:2﹣6=k,
解得:k=﹣4,
故答案为:﹣4
19.解:根据图示可得,
故答案是:.
20.解:设小长方形的长为xmm,宽为ymm,
由题意,得:,
解得:,
则每个小长方形的面积为:25×15=375(mm2)
故答案是:375.
21.解:(1)∵x+2y﹣6=0,∴y=3﹣x
又因为x,y为正整数,
∴3﹣x>0,
即:x只能取2或4;
∴方程x+2y﹣6=0的所有正整数解:,;
(2)由题意得:,解得
把代入x﹣2y+mx+5=0,解得m=﹣;
(3)∵方程x﹣2y+mx+5=0总有一个固定的解,
∴x=0,y=2.5.
∴.
22.解:,
①+②×2得13x=13m,解得x=m,
把x=m代入①得m+2y=5m,解得y=2m,
把x=m,y=2m代入x﹣2y+1=0得m﹣4m+1=0,
解得m=.
23.解:设正方形a的边长为x,正方形b的边长为y,根据题意得:.
解得:.
答:正方形a的边长为4,正方形b的边长为7.
24.解:由题意得,
解得,
代入原方程组得,
解得.
所以mn=﹣3×3=﹣9.
25.解:(1)
将②变形得3(2x﹣3y)+4y=11
④
将①代入④得
3×7+4y=11
y=
把y=代入①得,
∴方程组的解为
(2)
由①得3(x+4y)﹣2z=47
③
由②得2(x+4y)+z=36
④
③×2﹣④×3得z=2
26.解:(1)设甲种商品的进价为a元,则
98﹣a=40%a.
解得a=70.
答:甲种商品的进价为70元;
(2)设该商场购进甲种商品x件,根据题意可得:
70x+80(50﹣x)=3800,
解得:x=20;
乙种商品:50﹣20=30(件).
答:该商场购进甲种商品20件,乙种商品30件.
(3)设小华在该商场购买乙种商品b件,
根据题意,得
①当过480元,但不超过680元时,480+(128b﹣480)×0.6=576,
解得b=5.
②当超过680元时,128b×0.75=576,
解得b=6.
答:小华在该商场购买乙种商品5或6件.
27.解:(1)设购买一件甲种商品需要x元,购买一件乙种商品需要y元,购买一件丙种商品需要z元,
根据题意得:,
解得:,
∴x+y+z=90.
答:购甲、乙、丙三种商品各一件共需90元.
(2)小丽的说法正确.
设购买一件甲种商品需要x元,购买一件乙种商品需要y元,购买一件丙种商品需要z元,
根据题意得:,
方程①×3﹣方程②×2,得:x+y+z=90.
答:购甲、乙、丙三种商品各一件共需90元.
(3)设购买一套A教具需要a元,购买一套B教具需要b元,购买一套C教具需要c元,购买一套D教具需要d元,
根据题意得:,
方程组可变形为:,
设a+b+c+d=m,2b+3c+4d=n,
则原方程组可变形为:,
解得:,
∴5a+3b+2c+d=5(a+b+c+d)﹣(2b+3c+4d)=5m﹣n=3982.
答:购A教具5件、B教具3件、C教具2件、D教具1件共需3982元
1.若|x﹣y﹣1|+3(x+y)2=0,则x、y的值为( )
A.x=0.5,y=0.5
B.x=﹣0.5,y=﹣0.5
C.x=﹣0.5,y=0.5
D.x=0.5,y=﹣0.5
2.一个两位数加18所得的数是它的个位数字与十位数字换了位置后的数,则这个两位数是( )A.13
B.13或14
C.有9种可能
D.有7种可能
3.两个缸内共有48桶水,甲缸给乙缸加水一倍,然后乙缸又给甲缸加甲缸剩余水的一倍,则两缸水量相等同,问最初两缸内各有水( )桶.
A.30桶,16桶
B.15桶,18桶
C.30桶,18桶
D.30桶,12桶
4.若关于x,y的方程组没有实数解,则( )
A.ab=﹣2
B.ab=﹣2且a≠1
C.ab≠﹣2
D.ab=﹣2且a≠2
5.如果,则2x:3y等于( )
A.﹣2
B.
C.2
D.
6.已知实数x、y、z满足3x+7y+z=5,4x+10y+z=3,则x+y+z=( )
A.9
B.10
C.12
D.不确定
7.方程x+2y=7在自然数范围内的解( )
A.有无数个
B.只有一个
C.只有3个
D.以上都不对
8.如果一个三角形的三边a
b
c满足关系式+|a﹣b+2|+(c﹣10)2=0,那么这个三角形的形状为( )
A.锐角三角形
B.钝角三角形
C.直角三角形
D.以上都不对
9.有铅笔、练习本、圆珠笔三种学习用品,若购铅笔3支,练习本7本,圆珠笔1支共需3.15元;若购铅笔4支,练习本8本,圆珠笔2支共需4.2元,那么,购铅笔、练习本、圆珠笔各1件共需( )
A.1.2元
B.1.05元
C.0.95元
D.0.9元
10.若x=时,关于x,y的二元一次方程组的解x,y互为倒数,则a﹣2b=
.
11.如果1台大收割机和1台小收割机每小时各收割小麦x公顷和y公顷,那么2台大收割机和5台小收割机1小时收割小麦
公顷,3台大收割机和2台小收割机1小时收割小麦
公顷.
12.已知方程组中,x,y的值相等,则n=
.
13.若的解是方程ax﹣3y=2的一组解,则a的值是
.
14.某长方形的周长是44,若宽的3倍比长多6,则该长方形的长等于
.
15.寒假期间,爱学习的小明决定将部分压岁钱用于购买A、B两种文具,2月10日,A文具的单价比B文具的单价少2元,小明购进A、B两种文具共3件;2月20日,A文具的单价翻倍,B文具的单价不变,小明购进A、B两种文具共4件.若A、B文具的单价和数量均为正整数且小明第二次购买文具比第一次购买文具多花费5元,则小明两次购买文具共花费
元.
16.(黑龙江)写出满足方程x+2y=9的一对整数解
.
17.打折前,买50件A商品和30件B商品用了920元,买60件A商品和10件B产品用了1000元.打折后,买400件A商品和400件B商品用了7500元,比不打折时少花的钱数为
元.
18.若方程x﹣y=﹣1的一个解与方程组的解相同,则k的值为
.
19.如图,10块相同的小长方形墙砖拼成一个大长方形,设小长方形墙砖的长和宽分别为x厘米和y厘米,则列出的方程组为
.
20.小明在拼图时,发现8个一样大小的长方形,恰好可以拼成一个大的长方形如图(1);小红看见了,说:“我也来试一试.”结果小红七拼八凑,拼成了如图(2)那样的正方形,中间还留下了一个洞,恰好是边长为5mm的小正方形,则每个小长方形的面积为
mm2.
21.已知关于x,y的方程组
(1)请直接写出方程x+2y﹣6=0的所有正整数解;
(2)若方程组的解满足x+y=0,求m的值;
(3)无论实数m取何值,方程x﹣2y+mx+5=0总有一个固定的解,请直接写出这个解?
22.已知关于x,y的二元一次方程组的解满足方程x﹣2y+1=0,求m的值.
23.某校“数学建模”社团的同学用五个正方形拼成如图所示的无缝隙、不重叠的长方形,若中间小正方形的边长为1,求正方形a和b的边长.
24.已知关于x,y的方程组与的解相同,求mn的值.
25.阅读材料:善于思考的小明在解方程组时,采用了一种“整体代换”的解法,解法如下:
解:将方程②8x+20y+2y=10,变形为2(4x+10y)+2y=10③,把方程①代入③得,2×6+2y=10,则y=﹣1;把y=﹣1代入①得,x=4,所以方程组的解为:
请你解决以下问题:
(1)试用小明的“整体代换”的方法解方程组
(2)已知x、y、z,满足试求z的值.
26.平价商场经销的甲,乙两种商品,甲种商品每件售价98元,利润率为40%;乙种商品每件进价80元,售价128元.
(1)求甲种商品每件的进价;(利润率=×100%)
(2)若该商场同时购进甲、乙两种商品共50件,恰好总进价为3800元,求购进甲、乙两种商品各多少件?
(3)在“元旦”期间,该商场只对乙种商品进行如表的优惠促销活动:
打折前一次性购物总金额
优惠措施
少于等于480元
不优惠
超过480元,但不超过680元
其中480元不打折,超过480元的部分给予6折优惠
超过680元
按购物总额给予7.5折优惠
按表的优惠条件,若小华一次性购买乙种商品实际付款576元,求小华在该商场购买乙种商品多少件?
27.问题:有甲、乙、丙三种商品,①购甲3件、乙5件、丙7件共需490元钱;②购甲4件、乙7件、丙10件共需690元钱;③购甲2件,乙3件,丙1件共需170元钱.求购甲、乙、丙三种商品各一件共需多少元?
小明说:“可以根据3个条件列出三元一次方程组,分别求出购甲、乙、丙一件需多少钱,再相加即可求得答案.”
小丽经过一番思考后,说:“本题可以去掉条件③,只用①②两个条件,仍能求出答案.”针对小丽的发言,同学们进行了热烈地讨论.
(1)请你按小明的思路解决问题.
(2)小丽的说法正确吗?如果正确,请完成解答过程;如果不正确,请说明理由.
(3)请根据上述解决问题中积累的经验,解决下面的问题:学校购买四种教学用具A、B、C、D,第一次购A教具1件、B教具3件、C教具4件、D教具5件共花2018元;第二次购A教具1件、B教具5件、C教具7件、D教具9件共花3036元.求购A教具5件、B教具3件、C教具2件、D教具1件共需多少元?
参考答案
1.解:依题意得:,
由(1)得:x=y+1…(3),
将(3)代入(2)中得:y+1+y=2y+1=0,
y=﹣0.5…(4).
将(4)代入(3)得:x=0.5.
故选:D.
2.解:设原两位数的十位数字为a,个位数字为b,
则10a+b+18=10b+a,
∴b﹣a=2,
∴b=a+2.
a可取1,2,3,4,5,6,7,
故有7种可能.
故选:D.
3.解:设甲有x桶,乙有y桶,
,
.
甲缸内有水30桶,乙缸有水18桶.
故选:C.
4.解:,
由①得,x=﹣1﹣ay,
代入②得,b(﹣1﹣ay)﹣2y+a=0,
即(﹣ab﹣2)y=b﹣a,
因为此方程组没有实数根,所以﹣ab﹣2=0,ab=﹣2.
故选:A.
5.解:在中,
①×4﹣②,得3x=9,
x=3.
代入①,得y=1.
∴2x:3y=2×3:3×1=2.
故选:C.
6.解:由x、y、z满足3x+7y+z=5和4x+10y+z=3,
得出:,
解得:,
故选:A.
7.解:由已知,得y=,
要使x,y都是自然数,
合适的x值只能是x=1,3,5,7,
相应的y值为y=3,2,1,0.
∴解为,,,.
故选:D.
8.解:∵+|a﹣b+2|+(c﹣10)2=0
∴,
解得:,
则这个三角形的形状为直角三角形,
故选:C.
9.解:设购一支铅笔,一本练习本,一支圆珠笔分别需要x,y,z元,
根据题意得,
②﹣①得x+y+z=1.05(元).
故选:B.
10.解:由于x、y互为倒数,x=,则y=2,
代入二元一次方程组,
得,
解得a=10,b=﹣,
则a﹣2b=11.
故本题答案为:11.
11.解:由于1台大收割机和1台小收割机1小时各收割小麦x公顷和y公顷.
根据题意得么2台大收割机和5台小收割机1小时收割小麦
(2x+5y)公顷,3台大收割机和2台小收割机1小时收割小麦(3x+2y)公顷.
故答案为(2x+5y),(3x+2y).
12.解:由解得,
∴5x﹣4y=5﹣4=1.
故答案为1.
13.解:解方程组得:,
把代入方程ax﹣3y=2得:﹣a﹣6=2,
解得:a=﹣8,
故答案为:﹣8.
14.解:设长方形的长为x,宽为y.
则,
解得.
则该长方形的长等于15.
故填15.
15.解:设B文具的单价为x元/件,第一次购买文具共花费y元,
依题意,得:
①当第一次买A文具1个,第二次买A文具1个,
,
解得:,不合题意舍去.
②当第一次买A文具1个,第二次买A文具2个,
,
解得:,不合题意舍去.
③当第一次买A文具1个,第二次买A文具3个
,
解得:,不合题意舍去.
④当第一次买A文具2个,第二次买A文具1个
,
解得:,不合题意舍去.
⑤当第一次买A文具2个,第二次买A文具2个
,
解得:,符合题意.
⑥当第一次买A文具2个,第二次买A文具3个
,
解得,不合题意舍去.
∴x=3,y=5,
∴y+y+5=15.
故答案为:15.
16.解:假设y=1,
把y=1代入方程得:x=7,
∴是方程x+2y=9的一对整数解.
17.解:设打折前A商品每件x元,B商品每件y元,根据题意得:
,
解得:,
则打折前买400件A商品和400件B商品需要400×16+400×4=8000(元),
则打折后比打折前少花8000﹣7500=500(元).
故答案为:500.
18.解:联立得:,
解得:,
代入方程得:2﹣6=k,
解得:k=﹣4,
故答案为:﹣4
19.解:根据图示可得,
故答案是:.
20.解:设小长方形的长为xmm,宽为ymm,
由题意,得:,
解得:,
则每个小长方形的面积为:25×15=375(mm2)
故答案是:375.
21.解:(1)∵x+2y﹣6=0,∴y=3﹣x
又因为x,y为正整数,
∴3﹣x>0,
即:x只能取2或4;
∴方程x+2y﹣6=0的所有正整数解:,;
(2)由题意得:,解得
把代入x﹣2y+mx+5=0,解得m=﹣;
(3)∵方程x﹣2y+mx+5=0总有一个固定的解,
∴x=0,y=2.5.
∴.
22.解:,
①+②×2得13x=13m,解得x=m,
把x=m代入①得m+2y=5m,解得y=2m,
把x=m,y=2m代入x﹣2y+1=0得m﹣4m+1=0,
解得m=.
23.解:设正方形a的边长为x,正方形b的边长为y,根据题意得:.
解得:.
答:正方形a的边长为4,正方形b的边长为7.
24.解:由题意得,
解得,
代入原方程组得,
解得.
所以mn=﹣3×3=﹣9.
25.解:(1)
将②变形得3(2x﹣3y)+4y=11
④
将①代入④得
3×7+4y=11
y=
把y=代入①得,
∴方程组的解为
(2)
由①得3(x+4y)﹣2z=47
③
由②得2(x+4y)+z=36
④
③×2﹣④×3得z=2
26.解:(1)设甲种商品的进价为a元,则
98﹣a=40%a.
解得a=70.
答:甲种商品的进价为70元;
(2)设该商场购进甲种商品x件,根据题意可得:
70x+80(50﹣x)=3800,
解得:x=20;
乙种商品:50﹣20=30(件).
答:该商场购进甲种商品20件,乙种商品30件.
(3)设小华在该商场购买乙种商品b件,
根据题意,得
①当过480元,但不超过680元时,480+(128b﹣480)×0.6=576,
解得b=5.
②当超过680元时,128b×0.75=576,
解得b=6.
答:小华在该商场购买乙种商品5或6件.
27.解:(1)设购买一件甲种商品需要x元,购买一件乙种商品需要y元,购买一件丙种商品需要z元,
根据题意得:,
解得:,
∴x+y+z=90.
答:购甲、乙、丙三种商品各一件共需90元.
(2)小丽的说法正确.
设购买一件甲种商品需要x元,购买一件乙种商品需要y元,购买一件丙种商品需要z元,
根据题意得:,
方程①×3﹣方程②×2,得:x+y+z=90.
答:购甲、乙、丙三种商品各一件共需90元.
(3)设购买一套A教具需要a元,购买一套B教具需要b元,购买一套C教具需要c元,购买一套D教具需要d元,
根据题意得:,
方程组可变形为:,
设a+b+c+d=m,2b+3c+4d=n,
则原方程组可变形为:,
解得:,
∴5a+3b+2c+d=5(a+b+c+d)﹣(2b+3c+4d)=5m﹣n=3982.
答:购A教具5件、B教具3件、C教具2件、D教具1件共需3982元
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
