浙教版数学七年级下册全册导学案

数 学
下 册
创造“绿色”成绩
学校的根本任务是培育人才，学校的中心工作是教学工作，教学质量是学校发展的生命线，教学质量的优劣关键在课堂，课堂高效率才有学校的高质量。
在新课程理念的指引下，我们积极探索“先学后教”的教学改革，努力提高课堂教学的有效性。经过各个教研组的认真研究，学校确定了以“导学稿”为抓手的课堂教学模式，实施两年来，课堂教学效益明显提高，学生的学科成绩进步显著。
我坚信，在导学稿的教学模式下，老师们会深入研究学生、研究课堂、研究课程，不断深化导学稿的内容并发挥其功能，为学生创造“绿色”分数，达成“轻负高质”的教学目标，不断提升学校的教学质量。
目录 CONTENTS
TOC \o "1-3" \h \z \u HYPERLINK \l "_Toc292703986" 第七册（下） 1
HYPERLINK \l "_Toc292703987" 第1章 三角形的初步认识 1
HYPERLINK \l "_Toc292703988" 1.1 认识三角形（1） 1
HYPERLINK \l "_Toc292703989" 1.1 认识三角形（2） 3
HYPERLINK \l "_Toc292703990" 1.2 三角形的角平分线和中线 5
HYPERLINK \l "_Toc292703991" 1.3 三角形的高 7
HYPERLINK \l "_Toc292703992" 1.4 全等三角形 9
HYPERLINK \l "_Toc292703993" 1.5 三角形全等的条件（1） 11
HYPERLINK \l "_Toc292703994" 1.5 三角形全等的条件（2） 13
HYPERLINK \l "_Toc292703995" 1.5 三角形全等的条件（3） 15
HYPERLINK \l "_Toc292703996" 1.6 作三角形 17
HYPERLINK \l "_Toc292703997" 第2章 图形和变换 19
HYPERLINK \l "_Toc292703998" 2.1 轴对称图形 19
HYPERLINK \l "_Toc292703999" 2.2 轴对称变换 21
HYPERLINK \l "_Toc292704000" 2.3 平移变换 23
HYPERLINK \l "_Toc292704001" 2.4 旋转变换 25
HYPERLINK \l "_Toc292704002" 2.5 相似变换 27
HYPERLINK \l "_Toc292704003" 第3章 事件的可能性 29
HYPERLINK \l "_Toc292704004" 3.1 认识事件的可能性导学稿 29
HYPERLINK \l "_Toc292704005" 3.2 可能性的大小 导学稿 31
HYPERLINK \l "_Toc292704006" 3.3 可能性和概率 32
HYPERLINK \l "_Toc292704007" 3.4 复习 34
HYPERLINK \l "_Toc292704008" 第4章 二元一次方程组 36
HYPERLINK \l "_Toc292704009" 4.1 二元一次方程 36
HYPERLINK \l "_Toc292704010" 4.2 二元一次方程组 38
HYPERLINK \l "_Toc292704011" 4.3 解二元一次方程组（1） 40
HYPERLINK \l "_Toc292704012" 4.3 解二元一次方程组（2） 41
HYPERLINK \l "_Toc292704013" 4.4 二元一次方程组的应用 42
HYPERLINK \l "_Toc292704014" 第5章 整式的乘除 44
HYPERLINK \l "_Toc292704015" 5.1 同底数幂的乘法（1） 44
HYPERLINK \l "_Toc292704016" 5.1 同底数幂的乘法（2） 46
HYPERLINK \l "_Toc292704017" 5.1 同底数幂的乘法（3） 48
HYPERLINK \l "_Toc292704018" 5.2 单项式的乘法 50
HYPERLINK \l "_Toc292704019" 5.3 多项式的乘法导学稿 52
HYPERLINK \l "_Toc292704020" 5.4 乘法公式（1） 54
HYPERLINK \l "_Toc292704021" 5.4 乘法公式（2） 56
HYPERLINK \l "_Toc292704022" 5.5 整式的化简 58
HYPERLINK \l "_Toc292704023" 5.6 同底数幂的除法（1） 60
HYPERLINK \l "_Toc292704024" 5.6 同底数幂的除法（2） 62
HYPERLINK \l "_Toc292704025" 5.7 整式的除法 64
HYPERLINK \l "_Toc292704026" 第6章 因式分解 66
HYPERLINK \l "_Toc292704027" 6.1 因式分解 66
HYPERLINK \l "_Toc292704028" 6.2 提取公因式法 67
HYPERLINK \l "_Toc292704029" 6.3 用乘法公式分解因式(1) 69
HYPERLINK \l "_Toc292704030" 6.4 因式分解的简单应用 73
HYPERLINK \l "_Toc292704031" 6.5 因式分解复习 75
HYPERLINK \l "_Toc292704032" 第7章 分式 76
HYPERLINK \l "_Toc292704033" 7.1 分式（1） 76
HYPERLINK \l "_Toc292704034" 7.1 分式（2） 78
HYPERLINK \l "_Toc292704035" 7.2 分式的乘除 80
HYPERLINK \l "_Toc292704036" 7.3 分式的加减（1） 81
HYPERLINK \l "_Toc292704037" 7.3 分式的加减（2） 82
HYPERLINK \l "_Toc292704038" 7.4 分式方程（1） 83
HYPERLINK \l "_Toc292704039" 7.4 分式方程（2） 85
HYPERLINK \l "_Toc292704040" 7.5 分式复习 87
第七册（下）
第1章 三角形的初步认识
1.1 认识三角形（1）
学习目标
1. 三角形的概念． 2．用符号、字母表示三角形．3．三角形任何两边之和大于第三边的性质。
二．回顾预习
1、定义：由不在 直线上的三条 首尾顺次连结所组成的图形，叫做三角形。
2、三角形的三要素是 、 、 。
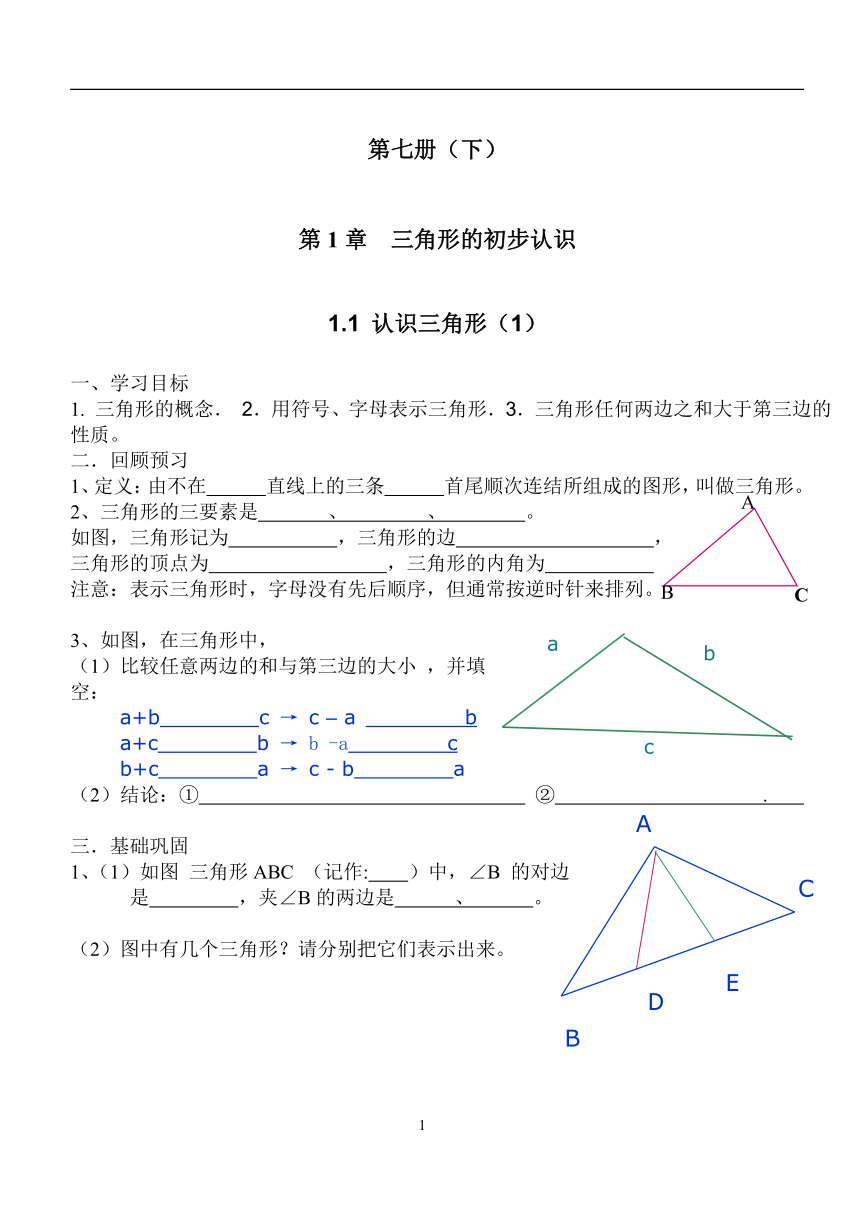
如图，三角形记为 ，三角形的边 ，
三角形的顶点为 ，三角形的内角为
注意：表示三角形时，字母没有先后顺序，但通常按逆时针来排列。
3、如图，在三角形中，
（1）比较任意两边的和与第三边的大小 ，并填空：
a+b c → c – a b
a+c b → b -a c
b+c a → c - b a
（2）结论：① ② .
三．基础巩固
1、（1）如图 三角形ABC （记作: ）中，∠B 的对边
是 ，夹∠B的两边是 、 。
（2）图中有几个三角形？请分别把它们表示出来。
2、已知四组线段：
第①组长度分别为5，6，11；第②组长度分别为1，4，4；；
第③组长度分别为4，4，4； 第④组长度分别为3，4，5，
其中不能成为一个三角形的三条边的是( )
A、① B、② C、③ D、④
3、已知一个三角形的两边长分别是1和5，则第三边C的取值范围是（ ）
A．1四．拓展提高
1、已知三角形两条边长分别为12cm和6cm，第三边与其中一边长相等，那么这个三角形的周长为多少cm？
2、现有长度分别为2cm，3cm，4cm，5cm的木棒，从中任取三根，组成三角形架，有几种情况？分别写出每组数据。
1.1 认识三角形（2）
学习目标
1、 理解三角形三个内角的和等于180o。
2、理解三角形的一个外角等于和它不相邻的两个内角的和。
3、合适用三角形的内角和外角的性质简单的几何问题
4、了解三角形的分类
二、回顾预习
1、三角形三边的性质: 。
2、角的分类： 、 、 、 、 。
3、三角形的内角和定理： 。
几何表示：在△ABC中，∠A+∠B+∠C= 。
5、如图
（1）△BCD的外角是_____
（2）∠2既是______的内角， 又是______的外角。
（3）∠2= + ∠1 > 或∠1 >
(4)三角形的外角与不相邻内角的关系：
① ，
② 。
三、基础巩固
1、在△ABC中 (1)若∠A=45°，∠B=30°，则∠C= .
变式1：在△ ABC中，∠A=45°，∠B= 2∠C，求∠B、 ∠C的度数。
变式2：在△ ABC中，∠A=∠B= 2∠C，求∠B、 ∠C的度数。
变式3：在△ ABC中，∠A：∠B：∠C=2：3：5，求∠A 、∠B、 ∠C的度数。
变式4：在△ ABC中，∠A+ ∠B = ∠C ，求∠C的度数。
2、在△ABC中，∠ACD是 外角.
(1)若∠A=74°，∠B=42°，则∠ACD= .
(2)若∠ACD=114 °36′，∠A=65°，则∠B= .
四、拓展提高
已知 ∠1, ∠2, ∠ 3是 △ABC三个外角,
则 ∠1+ ∠2+ ∠3=
1.2 三角形的角平分线和中线
学习目标
三角形的角平分线、中线的定义及画图。
利用三角形的角平分线和中线的性质解决有关的计算问题。
回顾预习
1．把一个角分成两个相等的 线叫做这个角的平分线。在三角形中，一个内角的角平分线与它的对边相交，这个角的顶点与交点之间的 叫做三角形的 。一个三角形共有 条角平分线，它们相交于 点。
（1）
（2）
2．已知如图（1），AD是△ABC的平分线，
①则 = = ，②若∠BAC=800，则∠BAD= ，
∠CAD= 。
3．在三角形中，连结一个顶点与它对边 的线段，叫做这个三角形的 ，一个三角形共有 条中线，它们相交于 点。
4．已知如图（2），AD是△ABC中BC是的中线，
则①BD DC BC，
②S△ABD S△ADC S△ABC，
③若BC=8cm，则BD= ，CD= 。
5．请在△ABC中画出三个角的平分线，在△DEF中画出三条中线。
三．基础巩固
1．如图，在△ABC中，AD是∠BAC的平分线，已知
∠B=300，∠C=400，则∠BAD= 度。
变式：∠BAC=900，AD平分∠BAC，∠C=400，则
∠ADB的度数是 。
2．已知△ABC中，AC=5cm。中线AD把△ABC分成两个小三角形，且△ABD的周长比△ADC的周长大2cm。你能求出AB的长吗？
变式1：若将条件变为：“这两个小三角形的周长的差
是2cm”，你能求出AB的长吗？
变式2：已知△ABC中，AD是△ABC的中线，AC=8cm，
AB= 5cm，求△ADC与△ABD的周长差？
四、拓展与提高
如图，在△ABC中，BO、CO分别是∠ABC、∠ACB的平分线。
（1）若∠ABC=600，∠ACB=500，求∠BOC的度数。
（2）若∠A=600，求∠BOC的度数。
（3）若∠A=，求∠BOC的度数（用的代数式表示）。
1.3 三角形的高
一、学习目标：
1、经历折纸和画图等实践过程，认识三角形的高；
2、会画任意三角形的高；
3、会用三角形高的知识解决简单的实际问题。
二、回顾预习：
1、如图，在△ABC中，AD⊥BC垂足为点D ，则
称AD是 。
2、如图，AE为△ABC的高，∠C=30、∠BAC=80°，则
∠CAE= ，∠BAE= ，
∠B= 。
3、一个三角形有 高。
4、用三角尺分别画出图中锐角△ABC，直角△DEF，钝角△PQR的各边上的高。
总结：
（1）锐角三角形的三条高都在三角形的 ，垂足在相应顶点的对边上
且三条高相交于 点；
（2）直角三角形的斜边上的高在三角形的 ，一条直角边上的高是另
一条直角边，三条高相交于 ；
（3）钝角三角形的钝角所对的边上的高在三角形的 ，另两条边上的高
均在三角形的 ，三条高的延长线也相交于 点。
三、基础巩固：
1．下列各组图形中，哪一组图形中AD是△ABC 的高( )
2.如图在三角形ABC中,AD是三角形ABC的高,AE是∠BAC的角平分线.
已知∠ BAC=82°, ∠ C=40°,(1)求∠ DAE的大小.(2)若AE是中线且BC=10，AD=4，图中有面积相等的三角形吗？面积是多少？
四、拓展提高：
1.如图，点D、E、F分别是△ABC的三条边的中点，设△ABC的面积为S，
（1）连结AD，△ADC的面积是多少？
（2）由（1）题，你能求出△DEC的面积吗？△AEF
和△FBD的面积呢？
（3）求△DEF的面积
2.试把一块三角形煎饼分成大小相同的4块，有多少种分法？
1.4 全等三角形
一、学习目标：
1、了解全等图形的概念，会用叠合等方法判定两个图形是否全等。
2、知道全等三角形的有关概念，能在全等三角形中正确地找出对应顶点、对应边、
对应角。
3、会说出全等三角形的性质
二、回顾预习：
1、能够 的两个图形叫全等形；
2、两个全等三角形重合时，互相重合的顶点做 ；互相重合的边叫
做　 　　；互相重合的角叫做　　 　；
3、全等三角形对应边　 　，对应
角　 　；　
4、记两个三角形全等时，通常把表示对应顶点
的字母写在 ；例如△ABC
≌ △DEF ，对应顶点分别是 ；
5、若△AOC≌△BOD，AC的对应边是 ，AO的对应
边是 ，OC的对应边是 ；∠A的对应角
是 , ∠C的对应角是 , ∠AOC的
对应角是 。
注意：记两个全等三角形时，通常把表示对应顶点
的字母写在对应的位置上。
三、基础巩固：
1、找一找：
（1）、若△ABD≌△ACD，对应顶点是 ，
对应角是 ；
对应边是 ；
（2）、若△ABC≌△CDA, 对应顶点是 ，
对应角是 ；
对应边是 ；
（3）、若△AOC≌△BOD，对应顶点是 ，
对应角是 ；
对应边是 ；
2、如图，在△ABC中，AD⊥BC于点D，BD=CD，则∠B= ∠C，请完成下面的说理过程。
解：∵AD⊥BC（已知）
∴∠ADB= =Rt∠（垂线的意义）
当把图形沿AD对折时，射线DB与DC ，
∵BD=CD（ ），
∴点B与点 重合，
∴△ABD与△ACD ，
∴△ABD △ACD(全等三角形的意义)，
∴∠B=∠C（ ）。
四、拓展提高：
如图，将△ABC绕其顶点A逆时针旋转30 o后，得△ADE。
（1）、△ABC与△ADE的关系如何？
（2）、求∠BAD的度数
（3）、求证 ∠CAE=∠BAD
1.5 三角形全等的条件（1）
学习目标
探索并掌握两个三角形全等的条件：有三边对应相等的两个三角形全等。
掌握角平分线的尺规作图
复习与回顾
1、如图若△ABC与△DEF全等，
记作△ABC △DEF。
其中∠A= ，∠B= ， =∠F，
BC= ， =DF，AB= 。
2、用圆规和直尺画△ABC，使AB=2cm. BC=1.5cm AC=2.5cm。并回答问题：
（1）、对比你与同学所画的三角形，它们能重合吗？
（2）、从作图可知，满足怎样条件的两个三角形能重合？
3、日常生活中，大桥的钢梁、起重机的支架等，都采用三角形的结构，是因为三角形具有 性。
4、全等三角形的判定条件1：有 的两个三角形全等，
简称 或 。
5、如图，在△ABC与△ABD中
AB= 。
∵ CA= 。
=BD
∴△ABC≌ △ABD （ ）
二、基础巩固
1、如图，已知AC=DB,要使△ABC≌△DCB,由“SSS”
可知只需再补充条件（ ）
A、BC=CB B、OB=OC C、AB=DC D、AB=BD
2、如图、点B、E、C、F在同一条直线上。且AB=DE，AC=DF，BE=CF。请将下面的过程和理由补充完整
解：∵BE=CF( )
∴BE+ =CF+ 既BC= .
在△ABC和△DEF中，
∵ AB= ( )
=DF( )
BC= ( )
∴△ABC≌△DEF( )
3、如图，AB=AC,BD=CD,则∠B=∠C,请说明理由。
4、如图，AB=CD,AD=AC,AC与BD相交于点O，
则图中的全等三角形共有 （ ）
A.2对 B.1对 C, 3对 D. 4对
变式1：BD是∠ABC的 线。
变式2：BE=BF，ED=FD，在图中
作出∠B的平分线。
变式3：用直尺和圆规作出∠ABC的平分线
三、拓展提高
如图，△ABC中，已知AB=AC，当点D是BC的 时，
可得△ABD≌△ACD。此时AD与BC的位置关系
是 。
1.5 三角形全等的条件（2）
学习目标
会运用“SAS”判定两个三角形全等
理解线段垂直平分线的性质
二．回顾预习
1、星期天，小刚在家玩蓝球，不小心将一块三角形玻璃摔
坏了（如图所示）。情急之中，小刚量出了AB、BC的
长，然后便去了玻璃店，他 （能或不能）重
新裁得一块和原来一样的三角形玻璃？于是向家里的弟
弟打电话，小刚还需询问一个数据就能如愿，这个数据
可以是_______。
2、有一个角和 对应相等的两个三角形全等，
简称 或 。
3、动手做一做：用量角器和刻度尺画 ，使 AB=4cm,BC=6cm,
将你画出的三角形和其他同学画的三角形进行比较，它们互相重合吗？
三、基础巩固
1、如图，点D、E分别在AC、AB上。已知AB=AC，
AD=AE，则BD＝CE。请说明理由。
解：在⊿ABD和 中，
AD = (已知)
= （公共角）
AB = AC（ ）
∴ ≌ ( )
∴ BD = CE（ ）
补：若BD=5,EF=1,则FC=( )
2、如图，已知B，C，E在一直线上，
∠1=∠2，AC=DC，说出AB=DB的理由 。
3、如图，O是线段AB的中点，直线m⊥AB于O,
则直线m是线段AB的 。
AO= .CA= .
4、如图，△ABC中，DE是AB的垂直平分线，
EC=2,EB=5,则AC= .
5、如图，线段AC、AB的中垂线交于点O，已知OC=2,
那么OB的长为（ ）
A. 1 B. 2 C.4 D. 不能确定
6、如图所示，A,B,C,表示三个村庄，现要在三个村庄
之间建一个仓库，使仓库到三个村庄的距离相等，请
在图中画出仓库的位置。
四、拓展提高
1、如图，△ABC中，D是BC上一点，AD=AC，
小明认为这个条件可以证明△ABC≌△ABD，
证：如图，在△ABC和△ABD中
AB=AB(公共边)
∠B=∠B （公共角）
AC=AD （已知）
∴△ABC≌ △ABD (SAS)
但证完了却又觉得不对，但又不知道错哪儿了，你能帮他解决这个问题吗？
1.5 三角形全等的条件（3）
学习目标
会运用“ASA”判定两个三角形全等
理解角平分线的性质
二回顾预习
1、如图1，已知AD=AC，BD=BC，则△ABC≌△ABD，依据是 。
2、如图，已知AO=BO，CO=DO，则△AOC≌△BOD依据是 。
3、小明不小心将一块三角形模具打碎了，他是否可以只带其中的一块碎片到商店去，就能配一块与原来一样的三角形模具呢？如果可以，带 合适？
4、如图，在△ABE与△DCE中
∠B=∠C
BE= .
∠AEB= .
∴△ABE≌ .( )
5、如图，在△ABF与△CDE中，已知∠A=∠C,
∠B=∠D,DE=BF.求证：△ABF≌△CDE 。
证：∵∠A=∠C,∠B=∠D.∴∠AFB= .
在△ABF与△CDE中
∠AFB=
BF=
∠B=
∴△ABF≌△CDE( )
6、如图，已知∠B=∠C,要使△ABE≌△ACD,
则需添加的条件可以是 。
7、如图，∵OD平分∠AOB,DE OA,DF OB.
∴ = .
(角平分线的点到角的两边的 相等)
三、基础巩固
8、如图，已知∠C=∠D,AB平分∠DBC,请说明AC=AD
的理由。
9、已知∠A=∠,∠B=∠,AB=,则△ABC≌△的依据是（ ）
A. SAS B. SSA C. ASA D. AAS
10、如图，已知∠ABC=∠DCB, ∠ACB=∠DBC,
由此可判定三角形全等的是（ ）
A. △ABD≌△DCO B. △ABC≌△DCB
C. △ABD ≌△BCA D. △OAD≌△OBC
11、如图∠ACB=∠DFE，BC=EF，根据ASA或
AAS，那么可以补充条件 ，就能使△ABC≌△DEF
12、如图，△ABC中，∠C=90°,AC=40cm,BD平分∠ABC,DF⊥AB于F,AD:DC=5:3
则D到AB的距离为 cm.
13、判断下列条件能否使△ABC≌△
（1）∠A=30°，∠B=45°，AB=2cm，∠=45°，∠=80°=2cm ( )
(2) ∠A=25°，∠B=30°,BC=2cm, ∠=25°,∠=30°=2cm ( )
(3) ∠A=∠,∠B=∠,BC= ( )
(4) ∠A=∠, AB=，BC= ( )
四拓展提高
如图，△ABC的角平分线BE、CF相交于O点，那么点O到△ABC三边的距离相等，请说明理由。
1.6 作三角形
学习目标
了解尺规作图的含义及其历史背景
会一些的尺规作图
二预习回顾
1.如何画一个角等于下面这个角？
2.　已知∠1、∠2和线段a，用尺规作，使
三基础巩固
1、已知线段，用尺规作使得。
a b c
2、已知线段，用尺规作使得
3、利用尺规不能唯一作出的三角形是（ ）
A、已知三边 B、已知两边及夹角 C、已知两角及夹边 D、已知两边及其中一边的对角
4、利用尺规不可作的直角三角形是 （ ）
A、已知斜边及一条直角边 B、已知两条直角边
C、已知两锐角 D、已知一锐角及一直角边
5、以下列线段为边能作三角形的是 （ ）
A、2厘米、3厘米、 5厘米 B、4厘米、4厘米、9厘米
C、1厘米、2厘米、 3厘米 D、2厘米、3厘米、4厘米
6、已知线段AB，用直尺和圆规作线段AB的垂直平分线。
四、拓展提高
1、有 A, B ,C 三农户准备一起挖一口
井，使它到三农户家的距离相等. 这口
井应挖在何处？请在图中标出井的位
置，并说明理由.
2、如图，直线l表示一条公路，点A和点B表示两个村庄。现要在公路上造一个加油站到两个村庄的距离相等，问加油站应建在何处？请在图上标明这个地点，并说明理由。
第2章 图形和变换
2.1 轴对称图形
学习目标
1．了解轴对称图形的概念和性质。
2．会判断一个图形是不是轴对称图形，并找出它的对称轴。
二、回顾预习
1．下列图形是轴对称图形吗？你是怎样判别的？对于以上的轴对称图形，请你画出对称轴。
2．轴对称图形的对称轴是一条 ；轴对称图形中沿对称轴
对折后能重合的两个点称为 。
3．轴对称图形的性质：对称轴 连结两个对称点之间的 。
三、基础巩固
1．下列图形是轴对称图形吗 如果是轴对称图形,请分别写出它们的对称轴.
线段： 角:
圆： 直角三角形：
长方形： 平行四边形：
2．在0 ，1，2，3，4，5 ，6 ，7 ，8 ，9 这几个数字中，哪几个是轴对称图形？
3．在26个英文字母中，有几个是轴对称图形？
ABCDEFGHIJKLMNOPQRSTUVWXYZ
4．你能举例说出汉字中是轴对称图形吗？（至少举3个）
四、拓展提高
如图，哪些图形是轴对称图形？哪些图形不是轴对称图形？如果是轴对称图形，请画出对称轴。
2．如图请用三种方法，在已知图案上再添上一个小正方形后，使其成为轴对称图形，并画出对称轴.
2.2 轴对称变换
学习目标
1．理解轴对称变换的性质，能按要求作出简单平面图形经过一至二次的轴对称变换。
2．掌握简单图形之间的轴对称关系。
回顾预习
1．下图是各种汽车的标志，其中是轴对称图形的有 个，并画出对称轴。
2.请画出下列图形关于直线m的对称图形：
.
（1） （2） （3）
3．结论：
(1)轴对称变换不改变原图形的 和 ，只改变 和 。
(2)轴对称变换的作图方法：1、 ,2、
3、 ，4、 。
（3）经轴对称变换所得的图形和原图形全等吗 。
4．镜子中出现的时间（如图），实际是几点？ 。
基础巩固
1．下列各组图中，左右两图不成轴对称的有 （ ）
A BC
2．小红驾驶着摩托车行驶在公路上，他从反光镜中看到后面一辆汽车的车牌为“”，根据有关数学知识，此汽车的牌照为______________
3．以直线m为对称轴,画出△ABC关于直线m的轴对称图形.
拓展提高
1．如图，AD是△ABC的一条角平分线，以直线AD为对称轴，将△ABC作轴对称变换，所得的像为△AB′C′。
(1)画出△AB′C′
(2)若∠C=70°, ∠B=42°,求∠C′DB的度数。
2．如图，将图形先以直线L1为对称轴作轴对称变换，再将所得的像连同原图形以直线L2为对称轴作轴对称变换，画出每次变换所得的像。
2.3 平移变换
学习目标
1．了解现实生活中图形的平移、图形平移变换的概念和图形平移变换的性质。
2．会按要求作出简单平面图形平移变换后的图形。
二、回顾预习
1下面两个图形的变换各是什么变换？
2．结论：
（1）由一个图形改变为另一个图形，在改变过程中，原图形上的所有的点都向 运动，且运动 ，这样的图形改变叫做图形的平移变换，简称 。
（2）平移变换的性质：平移变换不改变图形的 、 、和 。
连结对应点的线段 （ ）而且 。
3．如图经过平移，线段AB的端点A移到了点C，请你作出线段AB平移后的图形.。
三、基础巩固
1．如图，△ABC沿BA方向平移到△DEF所在的位置。
已知AB=3,AE=1,则△ABC平移的距离为 ，
点B的对应点为 。
2．将面积为30cm的等腰直角三角形ABC向下平移20cm，得到△MNP，则△MNP是 三角形，它的面积是 .
3．“小小竹排水中游，巍巍青山两岸走”，所蕴涵的图形变换是__________变换
4．若∠DEF是∠ABC经过平移得到的，∠ABC=33 ，则∠DEF= 。
四、拓展提高
1．在下面的方格纸中，画出一个Rt△ABC，使得∠B=Rt∠，BA=3，BC=4，再画出把所画的
Rt△ABC向右平移3个单位的像。
2． 已知△ABC如图，AB=AC,AD⊥BC于D.请设计一组关于△ADC的图形变换，使得最终所得的像与△ABD组成一个长方形（如图）。叙述这组变换过程，并画出每次变换后所得的图形。
2.4 旋转变换
学习目标
1．认识旋转变换的概念． 2．理解旋转变换的性质。
3．会按要求作出简单平面图形旋转变换后的像．
二、回顾预习
1．下列运动属于平移的是 （ ）
A.投篮时篮球的运动 B.空中放飞的风筝的运动
C.水管里水的流动 D.火车在一段笔直的铁轨上行驶
2．下列由数字组成的图形中，是轴对称图形的是（　 　）
3．小明在镜中看到身后墙上的时钟，实际时间最接近8时的是下图中的（　　）
4．将射线OP绕 ,按 时针方向旋
转 ,就得到射线OQ.
5．结论：（1）要描述一个旋转变换，必须指出：
、 、 。
（2）旋转变换不改变原图形的 和 。
（3）对应点到旋转中心的距离 。对应点与旋转
中心连线所成的角度等于 。
三、课堂巩固
1．△ACD是由△ABE旋转而得来,它们的旋转中心 是 ，旋转方向是 ，旋转角是 ，BE的对应边是 。
2．如图，四边形ABCD是正方形，△ADE旋转后能与△ABF重合．
（1）旋转中心是哪一点？
（2）旋转了多少度？
（3）如果连接EF，那么△AEF是怎样的三角形？
3．如图，画出三角形绕点O逆时针旋转90°后的三角形．
四、拓展提高
1．如图，已知图形F和点O，以点O为旋转中心，将图形按顺时针方向旋转90°，作出经旋转变换后的像．经几次旋转变换后的像可以与原图形重合？
2.一串有趣的图案按一定规律排列．请仔细观察，按此规律画出的第10个图案是 ；在前16个图案中有 个 ；第2008个图案是 .
2.5 相似变换
一、学习目标
1．认识相似图形和相似变换。
2．了解相似变换的基本性质，会按要求作出简单的图形（经过相似变换后的图形）。
二、回顾预习
1．下述图片的变换中具有哪些共同的特征？
（1） （2）
2．由一个图形改变为另一个图形,在改变的过程中保持 不变(大小可以改变),这样的图形改变叫做图形的相似变换.图形的 和 都是相似变换.原图形和经过相似变换后得到的像,我们称它们为 .
3．如图,把方格纸中的图形作相似变换,放大到原来的2倍,并在同一张方格纸中画出经变换后所得的新图象.
4． 把⊿ABC的每条边缩小到原来的1/2.
5．图形的相似变换不改变图形中每一个 的大小；图形中的每条 都扩大（或缩小）相同的倍数。
三、基础巩固
1.把如图所示的直角三角形ABC作相似变换,放大到原来的2倍.放大后所得的图形面积是原图形面积的多少倍？
2.（1）如图所提供的浙江省航线图可以
看做该省实际版图通过_______
变换所得到的图象.
（2）这个变换把实际版图缩小到原来
的___ __.
3.在沙漠中，一位旅行者带着罗盘和计程器从营地A出发，向北偏东37度方向行走３km,到达B地．然后他由B地出发，向正西方向行走5km，到达C地．比例尺为1:100000旅行路线图如下图所示：
(1) 确定你所画的路线图与实际路
线图经过那一种图形变化，缩小
的倍数是多少；
(2) 若要求旅行者返回营地的路线
最短，请在路线图上画出了旅行
者返回营地的路线．
第3章 事件的可能性
3.1 认识事件的可能性导学稿
一、学习目标
1．会根据经验判断一个事件是属于必然事件、不可能事件，还是不确定事件。
2．会用列举法统计简单事件发生的各种可能的结果数。
二、预习回顾
1．在标准大气压下，温度降到0℃以下时，水会结成冰，这个事件是 发生的。我们把这样的事件叫 事件。明年3月1日会下雨，这个事件是 发生的。我们把这样的事件叫 事件。用长为3CM、2CM、7CM的三根木条首位连接做成一个三角形，这个事件是 发生的。我们把这样的事件叫 事件。
2．盒子中放有形状、大小都相同的一个红球和一个白球：
（1）从中摸出一个球是蓝球是 事件，从中摸出一个球是红球是
事件。
（2）从中摸出一个球，可能摸到 球，也可能摸到 球，所以出现的结果有 种不同的可能。
（3）从中摸出一个球，记下颜色，放回，再摸出一个球，我们可用下面的树状图分析可能出现的结果：
从表中可知，这个事件可能出现的结果有①红、 ；②红、 ；
③ 、 ；④ 、 ：共 种。一般说；一个事件中，第一步有n种可能，第二步在第一步的每一种可能前提下都有m种可能，则这个事件共有 种可能。
三、巩固练习：
1．《每课必练》P27的1——7。
2．任意抛掷一枚硬币2次，朝上面共有多少种可能，用树状图表示出来。
四、拓展提高
1．《每课必练》P28的8、9题。
2.任意掷两枚普通的骰子，朝上面的数字共有几种不同的结果，朝上面的两个数字和为13的可能性有几种？两个数字和为偶数的可能性有几种？
3.2 可能性的大小 导学稿
班级 学号 姓名______
一、学习目标
会在简单情境下比较事件发生的可能性的大小
二、回顾预习
1．盒子中有8个红球和2个白球，从中任意摸一个球，因为红球个数比白球 ，所以，摸到红球的可能性 ；摸到白球的可能性 ；
2．如图，转动转盘一次，停止后指针落在 区域的可能
性大，是因为 。
3．如果把第1题中的10个球改成5个红球，5个白球，
摸到红球的可能性和摸到白球的可能性哪个大？答
4．任意抛掷一枚硬币，出现正面朝上和出现反面朝上的
可能性 。
5．在写有1-----9这9个数字的卡片中任意抽出一张，请把下列事件按可能性大小从大到小排列：（1）抽到整数。（2）抽到奇数。（3）抽到偶数。（4）抽到3的倍数。
（5）抽到7。
三、巩固练习
1．从1、2、3、2、3、4这几个数中任取一个，则取到 的可能性最大。
2．从一副扑克牌中任抽一张，可能性相同的是抽到（ ）
A. K和黑桃 B. 梅花和大王
C 大王和6 D. 10和A
3．《每课必练》P28的1——7。
四、拓展提高
1．《每课必练》P29的8题。
2．一个盒子中有10个大小相同的球，根据下列事件给定的可能性，
设计盒子中球的颜色。
（1）不可能摸到红球。
（2）摸到黄球的可能性大，摸到蓝球的可能性小。
（3）摸到白球的可能性最大，红球的可能性其次，黄球的可能性最小。
（4）摸到绿球和蓝球的可能性同样大，摸到黑球的可能性最小。
3.3 可能性和概率
一、学习目标
1．了解等可能性事件的概率公式。
2．会用列举法计算简单事件发生的概率。
二、预习回顾
1．必然事件发生的可能性是100％。所以必然事件发生的概率是 。不可能事件发生的可能性为零。所以不可能事件发生的概率是 。即若事件A是必然事件，则P(A)= .若事件B是不可能事件，则P(B)= 。
2．抛一枚硬币，出现的结果有 种，即是 面或 面，所以出现反面朝上的概率是 。出现正面朝上的概率是 。
3．掷一颗骰子，可能出现的结果有 种，那么数字6朝上的概率是 。
4．在一个装有5个红球，7个白球，8个黄球的盒子里任意摸出一个球，则：
（1）P（摸到红球）= 。
（2）P（摸到白球）= 。
（3）P（摸到黄球）= 。
5．从以上可知，一个事件共有m种可能，且每一种出现的可能性相同。若其中事件A有n种可能，则事件A的概率为P(A)= .
6．事件A发生的可能性越小，它的概率就越接近 。发生的可能性越大，它的概率就越接近 。所以随机事件A的概率范围是 ＜P(A)＜ .
三、巩固练习：
1．掷一枚骰子，则
（1）P（朝上数字为3）= 。
（2）P（朝上是2的倍数）= 。
（3）P（奇数朝上）= 。
（4）P（朝上的数小于5）= 。
2．如图一个黑白两色各占一半的转盘。
（1）若转动一次，指针落在白色区域的概率是 。
（2）连续转动两次，你能用画树状图的方法表示所有可
能结果吗？
指针指向区域共有 种不同结果，其中2次都指向黑色区域的结果
有 种，所以P（2次都指向黑色区域）= 。
（3）、连续转动两次，一次指向白色、另一次指向黑色的概率是 。
3．袋中装有3个绿球、5个黑球，它们除颜色外都相同，从中摸出一个球，记下颜色后放回，摇匀后再摸出一个球，用画树状图的方法计算下列事件的概率：
（1）两次都是绿球，（2）一次绿球、一次黑球，（3）两次都是黑球。
三、拓展提高：
小明和小刚玩游戏，他们各自从写有1----6这6个数字的卡片中抽出一张，然后把抽出的两个数相加，若和为偶数，则小明赢，否则小刚赢，这游戏公平吗？请说明理由.
3.4 复习
班级 学号 姓名______
一、知识回顾
1．下列事件中：确定事件是（ ）
A、掷一枚六个面分别标有1~6的数字的均匀骰子，骰子停止转动后偶数点朝上
B、从一副扑克牌中任意抽出一张牌，花色是红桃
C、任意选择电视的某一频道，正在播放动画片
D、在同一年出生的367名学生中，至少有两人的生日是同一天。
2．连续掷一枚硬币,结果1连8次正面朝上,那么第9次出现正面朝上的概率为________
A、0 B、1 C、1/2 D、不确定
3．如图所示，小明、小刚利用两个转盘进行游戏；规则为小明
将两个转盘各转一次，如配成紫色（红与蓝）得5分，否则小刚
得3分，此规则对小明和小刚（ ）
A、公平 B、对小明有利 C、对小刚有利 D、不可预测
4．有一个1万人的小镇，随机调查3000人，其中450人看中央电视台的晚间新闻，在该镇随便问一人，他（她）看中央电视台晚间新闻的概率是（ ）
A． B． C． D．
二、课内练习
1．从一副52张(去掉大、小王)的扑克牌中任意抽出一张，求下列事件的概率：
(1) 抽出一张红心________； (2)抽出一张红色老K________；
(3) 抽出一张梅花J________； (4)抽出一张不是Q的牌________
2．用2、3、4三个数字排成一个三位数，则排出的数是偶数的概率是________
3．如图是可自动转动的转盘(转盘被分成8个相等的扇形)。则指针指
向阴影区域的概率是________
4．某灯泡厂的一次质量检查，从2000个灯泡中抽查了100个，其中有8个不合格，则出现不合格灯泡的频率为______，在这2000个灯泡中，估计有______个灯泡为不合格产品.
5．依据闯关游戏规则，请你探究“闯关游戏”的奥秘：
（1）用列表的方法表示有可能的闯关情况；
（2）求出闯关成功的概率.
6.甲, 乙两人用下图所示的两个转盘做游戏, 转动两个转盘各一次.
（1）若转出的两个数字之和大于8则甲胜,否则乙胜,这个游戏公平吗 为什么
（2）若转出的两个数字和是偶数则甲胜,是奇数则乙胜,此时这个游戏公平吗 为什么
三、拓展提高
1．有木条五根，分别为12cm，10cm，8cm，6cm，4cm，从中任取三根能组成三角形的概率是（ 　）
A、 B、 C、 D、
2．一箱灯泡24个，合格率为87.5%，则小刚从中任意拿一个灯泡是次品的概率是（ ） A、1/24 B、87.5% C、0 D、1/8
3．如图若紫色、黄色、绿色区域面积分别为1、5、10,点D为线段BC中点.
有一只猫在三角形ABC内随意走动,则小猫停留在黑色区域的概率是_____。
4．如图，有两个可以自由转动的转盘A、B，转盘A被均匀分成4等份，每份标上数字1、2、3、4四个数字；转盘B被均匀分成6等份，每份标上数字1、2、3、4、5、6六个数字。有人为甲乙两人设计了一个游戏，其规则如下：
同时转动转盘A与B；
转盘停止后，指针各指向一个数字（如果指针恰好指在分割线上，那么重转一次，直到指针指向一个数字为止），用所指的两个数字作乘积，如果所得的积是偶数，那么甲得1分；如果所得的积是奇数，那么乙得1分。
你认为这样的规则是否公平？请你说明理由；如果不公平，请你设计一个公平的规则，并说明理由。
第4章 二元一次方程组
4.1 二元一次方程
一、学习目标
1.了解怎么样的方程是二元一次方程，理解什么叫二元一次方程的解。
2.能通过代入法判别有序数对是不是二元一次方程的解。
3.学会方程的变形。
二、回顾与学习
1．写出一个一元一次方程，并求出它的解。 。（你能说出一元一次方程及其解的概念吗）
2.试着列出方程（并观察与一元一次方程的区别）
(1)长方形的周长是34，要求长方形的长与宽，若设长为a，宽为b，
根据题意可得方程 。
(2)一场足球赛门票的收入共7400元，已知门票价格30元/人，学生优惠价10元/人，设观众中有学生x人，其余有y人，根据题意可得方程 。
3.上面的两个方程中有以下共同点：
①方程两边都是 式，②每个方程都有 个未知数，
③方程中含未知数的项的次数都是 次，符合以上条件的方程叫 。
4.把x=0.5,y=0代入方程2x-3y=1，
∵左边=2× -3× = ，右边= ，
∴左边 右边，∴x=0.5,y=0是方程的一个 ，记作 { 。
如果：再把x=2,y=1代入方程2x-3y=1, 左边 右边, 所以 也是方程的一个解，再换， 试一下，你能得出什么结论？结论是 。
三、基础巩固
1.下列方程是二元一次方程的是（ ）
(A)x2+y=0 (B)x= +1 (C) (D)y+
2.已知关于x、y的方程3x-2y=1是一个二元一次方程，则m= .
3.检验下列各组数值是不是方程2a=3b+20的解
① ② ③
4.已知方程2x+3y=2
(1)把方程变形成用含x的代数式表示y的形式。补全以下过程：
解：方程移项得：3y=　　　　　　　　　，
方程两边同除以3得：y＝　　　　　　　　　　　，
(2)把方程变形成用含y的代数式表示x的形式。
（３）根据所给的y值，求出相应的x的值，填入表内：
y 0 2 -2 1 …
x …
∴这个方程的解有 等
5.已知方程3x-2y=5
（1）用含x的代数式表示y。
　　
（2）用含y的代数式表示x。
　　
（3）写出方程的3个解。
四、拓展提高
1.写出解为的一个二元一次方程
2.已知,是方程2x+3y＝5的一个解，求a的值。
4.2 二元一次方程组
一、学习目标
1.懂得什么叫二元一次方程组。
2.理解什么是二元一次方程组的解，学会用尝试的方法求出二元一次方程组的解。
二、回顾与学习
1．小红买了面值为0.8元和1.5元的邮票共7张，刚好花了7元钱，求两种面值的邮票各多少张？
分析：
如果设面值0.8元的买了x张，面值1.5元的买了y张，
(1) 面值0.8元的买了x张共用去 元。面值1.5元的买了y张共用去 元。
（2）根据两种邮票共7张可得方程 。
（3）根据两种邮票共花了7元钱又程 。
（4）两个方程中的未知数x是表示同一个量吗？ y呢？
（5）像这样的两个方程，我们把它合起来写成 的方程组的形式。
2、在上题中得到的方程组中，整个方程组含有 个未知数，且两个方程都是 次方程，这样的方程组叫 方程组。
3.（1）已知方程x+y=200,填写下表
x … 85 90 95 100 105 …
y … …
（2）已知方程y=x+10，填写下表
x … 85 90 95 100 105 …
y … …
(3)由上可知， 既是方程x+y=200的解，又是方程y=x+10的解，
所以 是方程组 的解。
三、基础巩固
1.判断下列方程组是否是二元一次方程组的是（ ）
（A） (B) (C) (D)
2．方程组 的解是（ ）
（A） （B） （C） （D）
3．下列方程组中，解是 的方程组是（ ）
（A） （B） （C） （D）
4．某年级共有246名学生，男生比女生的2倍少2人，设男生x人，女生y人，则下列方程组正确的是 （ ）
A. B C D
四、拓展提高
1.．已知 是方程组 的解，求a、b的值
2.如图，用8块相同的长方形地砖能拼成一个大的长方形，
每个小长方形的长为x，宽为y；
（1）根据图中的数量关系列出关于x,y的方程组，
（2）写出这个方程组的解，
（3）求出大长方形的面积，
4.3 解二元一次方程组（1）
一、学习目标
1.弄清楚怎样把二元一次方程组的解能求出来。（化归思想）
2.学会代入消元法解二元一次方程组。
二、回顾与学习
1.方程2x+5=7的解是 ,方程2x+y=3可变形为y= .
2.已知二元一次方程2x+y=4,且y=x+1;则x= ,y= .
3.如果二元一次方程组的解是 .
4.二元一次方程组的解是 .
观察思考：把二元一次方程组化为一元一次方程，体现了化归的思想，达到 的目的，方法是采用了 ，这种解方程组的方法称为 法，简称 法。
三、基础巩固
1．已知，用含的代数式表示，得=______________.
2．已知3x+2y+4=0, 用含的代数式表示，得=______________．
3.用代入法解下列方程组
（1） （2）
四、拓展提高
解方程组
4.3 解二元一次方程组（2）
一、学习目标
学会加减消元法解二元一次方程组
二、回顾与学习
1.解二元一次方程组原则就是把二元一次方程变成一元一次方程，上节课通过
法达到消元的目的。
2.根据等式基本性质，现在方程2x+y=3两边都乘以2可得方程 。
3.如果A=B, C=D, 则A+C B+D (填 =或＞或＜)
4.把方程组等式的左边相加得到 ；右边相加得到 。
因为左边等于右边，所以可得 。最后可得
三、基础巩固
用加减法解下列方程组
1. 2.
3. 4.
四、拓展提高
1.关于x、y的二元一次方程组与的解相同，则
2.已知2v+t=3v-2t=3,求v、t的值
4.4 二元一次方程组的应用
一、学习目标
1.回顾列方程解应用题的基本步骤，当一元一次不能解决时尝试用二元一次方程组来解决。
2.理解列方程组解应用题的基本步骤。
3.学会用表格法分析问题。
二、回顾与学习
1.用简单的几个字概述一下列方程解应用题的步骤： 。
2.小明有5元和2元的人民币共50张，合计180元。若设5元人民币有x张，2元人民币有y 张，则可列方程组 .
3.两个数字，甲数比乙数的4倍少5，乙数比甲数的3倍多4，设甲数为a,乙数为b,则可列方程组 。
4.你能说出列方程组解应用题的一般步骤吗
三、基础巩固
1、香蕉的售价为5元/千克,苹果的售价为3元/千克,小华共买了9千克,付款33元.香蕉和苹果各买了多少千克？
售价 质量 付款
香蕉
苹果
2、甲、乙两人相距6千米，两人同时出发，若同向而行，则甲3小时可追上乙；若相向而行，1小时相遇，求两人的速度
S V t
同向 甲： 乙： 甲： 乙：
相向 甲： 乙： 甲： 乙：
四、拓展提高
小林骑自行车从甲地到乙地，先以24千米/小时的速度下坡，后以18千米/小时的速度通过平路，共花时间55分钟，返回时他以16千米/小时的速度通过平路，后又以8千米/小时的速度上坡，共1.5小时，求甲、乙两地的距离。
S V t
去 下坡： 平路： 下坡： 平路： 下坡： 平路：
来 坡： 平路： 坡： 平路： 坡： 平路：
第5章 整式的乘除
5.1 同底数幂的乘法（1）
一、学习目标：
1、理解同底数幂相乘的法则。
2、会运用同底数幂的乘法法则进行同底数幂相乘，并解决简单的实际问题。
二、回顾预习
1、表示 个a相乘，读做a的 次方，其中a叫做 ，n叫做 。底数是 ，指数是 。
2、= × × × × 。
3、计算：= ，= 。
4、根据幂的意义：（1）×=（ ）×（ ） ==
（2）×=（ ）×（ ）==
（3）×= （m、n都是正整数）
同底数幂的乘法法则：同底数幂相乘，底数 ，指数 。
5、下列计算是否正确？错的请改正：
（1）； （2）； （3） ；
（4） ； （5）； （6）。
三、巩固练习：
1、计算，并用幂的形式表示结果：
（1） ， （2），
（3） ， （4） ，
（5） ， （6）
2、 1克水中水分子的个数大约是3.34个，请估计相同条件下1千克水中含有水分子的个数（结果用科学记数法表示）。
3、计算：（1）；
（2）
四、拓展提高
1、已知 ， ，则 。
2、已知，且m-2n=1,求的值。
3、求下列各式中的x的值：
（1） ； （2） 。
5.1 同底数幂的乘法（2）
学习目标：
1、理解幂的乘方法则。 2、会运用幂的乘方法则进行计算。
3、会运用同底数幂的乘法法则和幂的乘方法则进行混合运算。
二、回顾预习：
1、根据乘方的意义和同底数幂的乘法法则填空：
归纳：幂的乘方法则：幂的乘方，底数 ，指数 。
即 （m,n都是正整数）
想一想： （填“＝”或“≠”）。
2、下面的计算对吗？错的请改正:
（6）
3、计算下列各式，结果用幂的形式表示:
（1） （2）=
（3）= （4）
三、基础巩固
1、说明下列每一步计算的理由，将它们填在括号内：
= （ ）
= （ ）
=
2、计算下列各式，结果用幂的形式表示:
（1） ； （2） ；
（3） ; (4) .
3、若一个正方体的棱长为，则这个正方体的体积为多少？
四、拓展提高
1、填空：（1） ； （2） ； （3） 。
2、已知 ，求n的值。
3、试比较 的大小。
5.1 同底数幂的乘法（3）
一 、学习目标：
1、理解积的乘方法则； 2、会计算积的乘方；
3、会进行简单的幂的混合运算。
二、回顾预习：
1、根据乘方的意义和同底数幂的乘法法则填空：
（1）(4 6) =（ ） （ ） （ ）
=（ ） （ ）
=
= =
（3）. ； （n为正整数）。
归纳：积的乘方法则：积的乘方,等于把积的每一个因式分别 ,再把所得 相乘。即 “积的乘方，等于 的积”。
2、下面的计算对吗？错的请改正:
3、木星是太阳系九大行星中最大的一颗，木星可以近似地看做球体。已知木星的半径大约是7×104 km，木星的体积大约是多少km3 ？（ p 取3.14）
三、基础巩固：
1、填空：①＝（ ） ； ②81=（ ） ；
③ ；④
2、计算下列各式，结果用幂的形式表示:
（1） ； （2） ；
3、用简便的方法计算：
（1） ； （2） ；
（3） 。
四、拓展提高：
1、若（a）=，那么m+n= .
2、若 ，求的值。
3、已知2x+4y-4=0,求(2x+4y)的值。
5.2 单项式的乘法
一、学习目标
1、掌握单项式与单项式、单项式与多项式相乘的法则.
2、理解单项式的乘法运算的算理，体会乘法的交换律、结合律及分配律的作用.
3、会运用单项式的乘法解决简单的实际问题.
二、回顾预习
1、填空：= ，= ，= ，=
= ， =
2、根据乘法交换律和结合律填空：
（1）、=（ ）（ ）=
（2）、=（ ）（ ）（ ） =
（3）、= +
（4）、=（ ）（ ）+（ ）（ ）=
归纳：单项式与单项式相乘的法则
单项式与单项式相乘，把它们的 、 分别相乘，其余 连同它的指数不变，作为积的因式。
判断正误，错的请改正。
（1） （2）
（3）（）（）= （4）
三、巩固练习
1、计算：
2、计算：
3、1cm干洁空气中大约有2.5×10个分子, 6×10cm干洁 空气中大约有多少个分子
四、拓展提高
1、已知： 则m= a= b=
2、如果xy x y 与-3xy是同类项,求4m-3n的值
5.3 多项式的乘法导学稿
一、学习目标
1、掌握多项式与多项式相乘的法则.
2、会运用单项式与单项式、单项式与多项式、多项式与多项式相乘的法则化简整式
二、回顾预习
1、填空：
(1)(-x)·(-x)·(-x) =______; (2) (x)=_______;(3) (xy)=______; (4)(xy)·(xy)·(xy) =______;(5) (-3xy)(-5xyz)= ;
(6)（b-3a）(-4a+3ab) =________________
2、下图是一间厨房的平面布局，我们可以用哪几种方法来表示此厨房的总面积？
（写出两种不同的表达方式）
1）
2）
结论：
归纳：多项式的乘法法则
多项式与多项式相乘, 先用一个多项式的 乘以另一个多项式的 , 再把所得的 .
3、计算：
(1) (x 1)(x +１) ； (2) (a-b)(c d)
(3) (3x+y)(x 2y) ； (4) (2a- 5b)(a+5b)
三、巩固练习
1计算：（1）、 （2）、
2、先化简，再求值：X=
四、拓展提高
1、观察下列各式的计算结果与相乘的两个多项式之间的关系：
(x+2)(x+3)=x+5x+6 ；(x+4)(x+2)=x+6x+8 ；(x+6)(x+5)=x+11x+30
(1)你发现有什么规律？按你发现的规律填空：
(x+3)(x+5)=x+(____+____)x +____×_____
(2)你能很快说出与(x+a)(x+b)相等的多项式吗？先猜一猜，再用多项式相乘的运算法则验证。
2.计算(x+2x-3x-5)(2x-3x+x-2)时,若不展开,求出x项的系数.
3、已知
求 的值
5.4 乘法公式（1）
一、学习目标
1、掌握平方差公式；会运用平方差公式进行多项式的乘法运算。
2、会运用平方差公式进行简便运算。
二、回顾预习
1、多项式与多项式相乘的法则: (a+n)(b+m)= 。
2、计算下列各题:
（1） (a+2)(a-2)=________________ （2） (3-x)(3+x)=________________
（3） (x+)(x-)=________________ (4) (2m+n)(2m-n)=_______________
结论：两数 与这两数 等于这两数的 。
即 (a+b)(a-b )=________________。
3、课本p116的“做一做”。
4、运用平方差公式计算:
(1) (3x+5y)(3x-5y) =____ – ____ =________
= - =
三、基础巩固
1、下列式子中哪些可以用平方差公式运算 如果可以,并计算：
⑴ (ab-8)(ab+8) ⑵
⑶ (2+a)(a-2) ⑷ (3a+2b)(3a-2b)
⑸ (-4k+3)(-4k-3) ⑹ (1-x)(-x-1)
⑺ (-x-1)(x+1) ⑻ (x+3)(x-2)
2、用平方差公式计算:
（1）102×98 (2)59.8×60.2 （3）50
3、一养鸡专业户改建一个边长为 a(m)的正方形养鸡场,计划纵向扩大3m,横向缩短3m,改建为长方形养鸡场.问改建后的养鸡场面积有没有变化 如果有变化,变化多少
四、拓展提高
1、运用平方差公式计算:
（1） （2）5678×5680-5679
（3）(2+1)(2+1)(2+1)(2+1)+1
2、如果则的值是（ ）
A、5 B、4 C、-4 D、以上都不是
5.4 乘法公式（2）
一、学习目标
1、掌握完全平方公式。
2、会用完全平方公式进行多项式的乘法公式。
二、回顾预习
1、用平方差公式计算:
（1）（x+8）(x-8)= ； （2）(2a+3)(2a-3)= ;
(3)(-3x+4y)(-4y-3x)= 。
2、请用多项式与多项式相乘的法则计算下列各式：
（1）（a＋b） （2）（a-b） （3）（2a＋x）
归纳：完全平方公式的文字叙述：两个数的和（或差）的 ，等于它们的 ，加上（或减去）它们的 的2倍。
数学表达式：(a+b) =
(a-b)= 。
3、填空：(1) (a+1) =( ) +2( )( )+( )
(2) (2a - 3b) =( ) - 2( )( )+( )
三、基础巩固：
1、利用完全平方公式计算：
（1）（3+x） (2) (y-7) (3) (3-t) （4）(-2x+y)
2、填空：
(1)（3x+2y)= +12xy+4y (2)(5m-4n)=25m-40mn+
(3)(4a+3b) =16a+ +9b (4)(2x-8y)=4x+ +64y
3、一花农有4块正方形茶花苗圃，边长分别为30.1m，29.5m，30m，27m。现将这4块苗圃的边长都增加1.5m，求各苗圃的面积分别增加了多少m ？
四、拓展提高：
1、已知a+b=3，ab=，求下列各式的值：
（1）； （2）； （3）。
2、一个正方形的边长增长5厘米，它的面积就增加35厘米，求这个正方形原来的边长。
3、若，则a、b的值分别为（ ）
A a=2,b=3 B a=-2, b=3 C a=-2,b=-3 D a=2,b=-3
5.5 整式的化简
学习目标：
1、掌握整式的加、减、乘、乘方混合运算的运算顺序
2、会利用加、减、乘、乘方运算将整式化简
3、会利用加、减、乘、乘方运算解决简单实际问题
二、回顾预习：
1、计算
（1）、 ， （2）、 ，
（3）、 ，（4）、 ，
（5）、 ，（6）、
2、如图：正方形ABCD与正方形PBEF中，M是AB中点，设AB=4a，MP=b，正方形APCD与正方形PBEF的面积之差为S
（1）、用a,b的代数式表示S
（2）、当a=4，b= 时，S的值是多少？
当a=5，b= 时呢？
三、基础巩固：
1填空：
（1）、 一块手表原价a元，降价x％，则现价为_______元。
（2）、一块手表原价a(1-x％)元，降价x％，则现价为 元。
（3）、一块手表原价a元，连续两次涨价x％，则现价为 元。
2、化简：
、
3、化简求值：
（1）、当 x=0.5 时，求代数式 的值
（2）、已知x=，求（-3x-1）（3x+1）+（-3x-1）（1-3x）的值。
4、解方程：
5、甲、乙两家超市3月份的销售额均为a万元，在4月和5月这两个月中，甲超市的销售额平均每月增长x％，而乙超市的销售额平均每月减少x％.
(1)、5月份甲超市的销售额比乙超市多多少？
(2)、如果a=150，x=2，那么5月份甲超市的销售额比乙超市多多少万元？
四、拓展提高
1、已知x+y=3，xy=1，求x+y与(x-y) 的值.
2、已知x+y -4x-6y+13=0,求x-y的值.
3、已知a-5a+1=0，求：（1） ， （2）的值
5.6 同底数幂的除法（1）
一、学习目标：
1、理解土地数米同底数幂相除的法则
2、会用同底数幂相除的法则进行同底数幂相除的运算
二、回顾预习：
1、填空：
= ，= ，=
2、计算:
= ，= ，=
3、请完成下列问题:
归纳：同底数幂的除法法则
同底数幂相除，底数_____, 指数______.
(a≠0,　 m、n都是正整数，且m>n)
4、下列计算对吗 为什么 错的请改正.
三、巩固练习：
1、计算
2、计算:
(3)a÷a·(-a) (4)(-x)÷(-x)
3、如图是洋葱的根尖细胞，细胞每分裂一次，1个细胞变成2个细胞。洋葱根尖细胞分裂的一个周期大约是12时，2个洋葱根类细胞经过分裂后，变成2个细胞大约需要多少时间？
四、拓展提高：
3、已知2x－5y－4=0，求4÷32的值。
5.6 同底数幂的除法（2）
一、学习目标：
1、了解零指数幂和负指数幂的概念，
2、会用零指数幂和负指数幂的意义进行计算，
3、会用科学记数法表示绝对值较小的数。
二、回顾预习：
1、同底数幂的除法的法则：同底数幂相除，底数 指数 ；即：a÷a=a（a≠0,m,n都是正整数，且m＞n）
2、填空：
（1）、x÷(-x)= ，（2）、a÷a= ，（3）、(y)÷y=
（4）、2÷(-2)= ， （5）、3÷(33)=
3、利用幂的意义和除法法则计算：
= ， ，
归纳：
（1）任何不等于零的数的零次幂都等于1。即= (a≠0)
（2）任何不等于零的数的-p(p是正整数)次幂,等于这个数的p次幂的倒数.
即= (a≠0,p是正整数)
4、下列计算对吗？为什么？错的请改正。
① (—3) = ② =1
③ 2= ④=0
⑤ =1 （a≠0）
5、找规律
1000000=10 100000=10 10000=10 1000=10
100=10 10=10 1=10 0.1==10
0.01==10 0.001==10 0.0001==10
三、巩固练习：
1、求下列各式的值
（1）、10 (2)、 3×3 (3)、(-3)
（4）、 (5)、 95×(-5) (6)、 a÷(-10)
(7) (-3)÷3 (8) (-0.5)
2、把下列各数表示成a×10（1≤a＜10，n为整数）的形式：
（1）、12000 （2）、0.0021 （3）、0.0000501
(4)、 325800 (5)、 0.000129 (6)、 0.00000087
3计算：
（1）、 （2）、 （3）、
四、拓展提高：
世界上最小、最轻的昆虫是膜翅目缨小蜂科的一种卵蜂体长仅0.021厘
米，其质量也只有0.000005克。
（1）、用科学记数法表示上述两个数据；
（2）、一个鸡蛋的质量大约是50克，多少只卵蜂的质量和与这个鸡蛋的质量相等？
5.7 整式的除法
一、学习目标：
1、掌握多项式除以单项式的运算法则，
2、掌握多项式除以单项式的运算法则，
3、会进行单项式除以单项式、多项式除以单项式，以及简单的乘除混合运算。
二、回顾预习：
1、用字母表示幂的运算性质：
2、计算：
3、根据除法法则计算：
（1）、
（2）、
（3）、 =
归纳：单项式与单项式相除的法则
单项式相除，把 、 分别相除，作为商的因式，对于只在 的字母，则连同它的指数作为商的一个因式。
4、填一填：
（1）、(625+125+50)÷25=( )÷( )+( )÷( )+( )÷( )
=( )+( )+( )
=( )
(2)、 (4a+6)÷2=( )÷2+( )÷2=( )
(3)、 (2a-4a)÷(-2a) =( )÷(-2a)+( )÷(-2a) =( )
归纳：多项式除以单项式法则
多项式除以单项式，先把这个多项式的每一项分别除以单项式，再把所得的商相加。
三、基础巩固：
1、下列错在哪里？应怎样改正？
（5）4a ÷2a= 2a （6）10a ÷5a=5a
（7）(-9x) ÷(-3x) =-3x （8）12ab ÷4a=3a
2、计算：
3、计算：
一个长方体模型的长、宽、高分别为4a(cm),3a(cm),2a(cm)。某种油
漆每千克可漆 的面积，问漆好这个模型需要多少油漆？
四、拓展提高
多项式一共有（ ）项，它除以，其商式应是（ ）项式，其商式为
第6章 因式分解
6.1 因式分解
一、学习目标
1.了解因式分解的概念和意义
2.了解因式分解与整式乘法的关系
二、回顾预习
1. 计算：（1）a (a + 1) = ； （2）（a + b）（a – b）= ；
（3）（a + 1） = .
2．把一个多项式转化为几个整式积的形式
(1) (2)a (3)
结论：把一个多项式化成几个整式积的形式,这种变形叫做把这个多项式 .
3.判断下列各式哪些是整式乘法？哪些是因式分解？
(1)
(2)2x(x-3y)=2
(3)(5a-1)=25a-10a+1
(4)+4x+4=
三、基础巩固
1．检验下列因式分解是否正确？
(1) (2)
2.计算下列各题，并说明你的算法
(1) (2)
四、拓展提高
1.已知多项式可分解为你能求出m的值吗？
6.2 提取公因式法
一、学习目标
1.会用提取公因式法分解因式。
2.理解添括号法则。
二、回顾预习
1.12、15这两数有公因数吗？ 是
2 .ma+mb+mc这个多项式中相同的因式是
3.多项式中各项都含有的相同因式,称之为
4.多项式3ax+6xyz有公因式吗？是什么？
5．请写出下列多项式的公因式。
3 2a+3ab 30mb+5nb
多项式3a的公因式是 ；
多项式15-6a的公因式是 ；
6.回顾去括号法则，完成下列填空：
(1) 1-x=+( ) (2) -x+1=-( )
(3) x-y=+( ) (4) -x-y =-( )
(5)( )
(6)a(s+t)-s-t=a(s+t)-( )
三、基础巩固
1、把下列各式分解因式
(1) (2) 6a
(3)8a-12ab
2.下列的分解因式对吗？如不对，请指出原因:
(1)2x (2) a
(3)-2s
(4) a
3.把下列各式分解因式：
(1) (2) 2a
(3)a (4)-3ab+abx-9aby
四、拓展提高
1.分解因式计算：
2.利用简便方法计算：
4.3
3.已知a+b=3, ab=2 ,求代数式a的值
4.把9分解因式
6.3 用乘法公式分解因式(1)
一、学习目标
1.会用平方差公式分解因式。
2.了解因式分解的思考步骤
二、回顾预习
1．平方差公式： =
2．下列多项式可以用平方差公式分解因式吗？若可以请分解。
(1) (2) (3)
3.把下列各式因式分解：
(1)16-1 (2)-m+4
(3) (4)
二、基础巩固
1、判断下列多项式可以用平方差公式分解因式吗？若2可以请分解。
(1) (2) (3)-4
(4)- (5) 4x-3 (6)
2.把下列各式分解因式
(1)25 (2)121-4a
(3)1-81 (4)a
3.分解下列因式
（1）4x3y－9xy3 （2）27a3bc－3ab3c
（3）（2n+1）2－（2n－1）2
解题反思：对于复杂的多项式，我们应该怎么做？
四、拓展提高
观察下表，你还能继续往下写吗？
1 1=1 －0
3 3=2 －1
5 5=3 －2
7 7=4 －3
… …
请写出下一个变化
你发现了什么规律，能用因式分解来说明你的发现吗？
（用含n的等式表示这一规律）
6.3 用乘法公式分解因式(2)
一．学习目标
1.会用完全平方公式分解因式。
2.会综合运用提取因式法、公式法分解因式。
二、回顾预习
1.把下列多项式因式分解
（1） （2）
2、按要求填表
完全平方式有什么特征：
3、把下列各式因式分解：
（1） a （2）4x
三、基础巩固
1、对下列多项式因式分解：
(1) (2) 3ax
(3)
四、拓展提高
1、你能用口算求出2005 -4010× 2003+2003 的值吗？
2、我们知道4x2+1不是完全平方式，有没有合适的项，你能给它补成完全平方式吗？
3、若，则求a、b的值.
4、已知：a +b +c -ab-bc-ac=0 则判断a，b，c的大小关系.
6.4 因式分解的简单应用
一 、学习目标
1.会运用因式分解进行简单的多项式除法。
2.会运用因式分解解简单的方程。
二、回顾预习
1.因式分解的几种方法：
(1).提取公因式法：
(2).公式法：应用平方差公式：
应用完全平方公式：a
2.因式分解：
(1)4 (2)2ab (3)xy-2x
3.计算：
(1) (2)
三、基础巩固
1.计算：
(1) (2)
2、解下列方程
(1)2x (2)
(3)4 (4)
四、拓展提高
1.解方程：
2．计算：
3．计算：
（1）
(2)
(3)
6.5 因式分解复习
一学习目标
1.了解分解因式的意义，会用提取公因式法、平方差和完全平方公式分解因式。
2.通过乘法公式的逆向变形，进步发展学生观察、归纳、类比、概括等能力。
二、回顾预习
1、因式分解的三大方法和四项注意：
方法：
注意：
2、因式分解：
（1）x y－4xy＋4y （2）
（3）(x －5) ＋2(x －5)＋1 （4）
（5）
三、基础巩固
1.试说明：任意四个连续整数的积与１的和是一个完全平方数．
2.若9x ＋2(a－4)x＋16是一个完全平方式,则a的值是 　　　　 .
3.不论a、b为何数，代数式a +b -2a+4b+5的值总是 （ ）
A.0 B.负数 C.正数 D.非负数
四、拓展提高
1、多项式9x +1加上一个单项式后,使它能成为一个整式的平方,则加上的单项式可以是_____________________(填上你认为正确的一个即可,不必考虑所有的可能情况).
2、甲、乙两同学分解因式x +ax+b时，甲看错了b，分解结果是(x+2)(x+6),乙看错了a，分解结果是(x+1)(x+16).请你分析一下a、b的值分别为多少，并写出正确的分解过程.
第7章 分式
7.1 分式（1）
一、学习目标：
1．能根据分式的概念，辨别出分式，理解当分母为零时，分式无意义。
2．能确定分式中字母的取值范围，使分式有意义，或使分式的值为零。
3．会用分式表示实际问题中的数量关系，并会求分式的值，体验分式在实际中的价值。
二、预习回顾：
1．用代数式表示
（1）为了调整珍稀动物资源，动物专家在p平方千米的保护区内找到7只灰熊，你能用代数式表示平均每平方千米保护区内有多少只灰熊吗？______
（2）某中学广场校区进行晨跑锻炼. 某位同学原来跑步速度为15千米/时,经过一段时间的锻炼后,速度加快了a千米/时,则该同学跑完b千米需 小时。
2．表示两个整式 ,且除式中含有 ,像这样的代数式就叫做分式
3．下列代数式中，哪些是整式？哪些是分式？
，，，，，
三、巩固练习：
1．填空:
(1)当 时,分式有意义;
(2)当 时,分式的值是零;
(3)当x=2时,分式没有意义,则 b=
(4) 要使分式没有意义,则的值是( )
(5) 要使分式有意义, x的取值满足( )
2．甲﹑乙两人从一条公路的某处出发，同向而行．已知甲每时行a千米，乙每时行b千米，a＞b．如果乙提前１时出发，那么甲追上乙需要多少时间？当a=6，b=5时，求甲追上乙所需要的时间？
四、拓展提高：
1．当x为任意实数时，下列分式一定有意义的是（ ）
（A） （B） (C) (D)
2．在分式中，当x为何值时，分式有意义？分式的值为零？若分式
3． 的值为0，则x的值是多少？
7.1 分式（2）
一、学习目标：
1．通过类比分数的基本性质，说出分式的基本性质，并能用字母表示。
2．理解并掌握分式的基本性质和符号法则。
3．能运用分式的基本性质和符号法则对分式进行变性和约分。
二、预习回顾：
1．当x取什么值时，下列分式有意义：
（1） （2）
2．分式的基本性质
分式的分子与分母都乘以（或除以）同一个不等于零的整式,分式的值 。
用式子表示是：
（其中M是不等于零的整式）
填一填：
= ， ，
3．在下列各式中，找出哪些是相等的分式？
(1) (2) (3) (4) (5)
归纳：分式的符号法则：
分子、分母及分式的符号，改变其中任何 个，分式的值不变。
三、巩固练习：
1．不改变分式的值，把下列各式的分子与分母中各项的系数都化为整数：
（1） （2）
2．不改变分式的值，使下列分子与分母都不含“－”号
3．不改变分式的值，把下列分式的分子与分母的最高次项的系数都化为正数：
4．化简下列分式：
（1） （2）
5．如图，为了制作贺卡,需在边长为（2b+2）的正方形纸片上剪下边长为2的正方形。若合理剪裁可将剩下的纸片恰好拼成一长为（b+2）的长方形,拼成的长方形的宽是多少
四、拓展提高：
1．已知 ，求 　 　　 的值
7.2 分式的乘除
学习目标
1.掌握分式的乘除法则
2.会进行分式的乘除运算，并会用来解决简单的实际问题。
回顾预习
1．约分:
2．根据分数的乘除法法则计算：（1） （2）
3．根据上述计算猜想填空： ； 。
分式的乘除法法则是 。
巩固练习
1.下面的计算对吗？如果不对，应如何改正？
（1） （2） （3） （4）
2．计算：
（1） （2）
（3） （4）
四、拓展提高
1．先化简，再求值：其中
7.3 分式的加减（1）
一、学习目标
1．掌握同分母分式加减的法则；2.会进行同分母分式的加减运算。
二、回顾预习
1．计算：（1）
类似地，
结论：同分母分式相加减，分母 ，把分子 。
三、巩固练习
1．填空：（1） ， （2） 。
2．计算：
（1） ， （2） ，
（3） ， （4） 。
3．先化简，在求值：，其中m=2011,n=-1.
四、拓展提高
1．若2x+y=0,求的值。
7.3 分式的加减（2）
一、学习目标
1．会进行异分母分式的通分；2.会进行异分母分式的加减运算。
二、回顾预习
1．先化简，再计算： ，其中x =6 。
2．计算：= ， 。
异分母分式加减的法则：先 ，把异分母分式化为 的分式，
然后再按同分母分式的加减法法则进行计算。
即 + = ， - =
三、巩固练习
1．计算：（1） ， （2） , （3）
（4） , （5） , (6)
四、拓展提高
7.4 分式方程（1）
一、学习目标
1．了解分式方程的概念； 2.会解可化为一元一次方程的分式方程；
3．了解增根的概念，会对分式方程进行根的检验。
二、回顾预习
1．判别下列方程各是什么方程：
2(x－1)=x＋1; ( ) x+2y=1 ( ); ( )
定义：方程中只含有 ,且分母含有 的方程叫做分式方程。
2．已知分式，当x 时, 分式无意义.
3．分式与的最简公分母是 ；分式与的最简公分母是 。
三、巩固练习
1．解方程去分母，化为整式方程，正确的是（　　）
2．解方程:
解:方程两边同乘以 ,
化简,得 .
解得 = , = .
检验:把x= ,代入最简公分母,
x(x-2)= = ≠0;
把= ,代入最简公分母：
x(x-2)= =0
∴x= 是增根,舍去. ∴原方程的根是x= .
3．解下列方程：
（1） （2） （3）
四、拓展提高
1．如果有增根,那么增根为 .。
2．若分式方程有增根x=2,则 a= 。
7.4 分式方程（2）
一、学习目标
1．会列分式方程解简单应用题； 2.会进行简单的公式变形。
二、回顾预习
1．甲、乙两人每时共能做35个电器零件，当甲做了90个零件时，乙做了120个，问甲、乙每时各做多少个电器零件？
分析：（1）每时做的零件数= ÷
（2）方程的等量关系： 。
（3）列出方程： 。
2．列分式方程解应用题的一般步骤：
、 、 、 、 、
3．下面的公式变形对吗？如果不对，应怎样改正？
将公式（1+ax≠0）变形成已知x，a，求b。
解：由 ，得 ，
∴ ，即 。
三、巩固练习
1．将下面的公式变形
（1） （用p和b 表示a） （2） （用f，v表示u）
2．工厂生产一种电子配件，每只的成本为2元，毛利率为25%，后来该工厂通过改进工艺，降低了成本，在售价不变的情况下，毛利率增加了15%，问这种配件每只的成本降低了多少元？（精确到0.01元）
分析：（1）本题等量关系是：
（2）售出价是：
（3）成本是：
(4) 根据等量关系，你能列出方程:
(5)解方程：
3．某班学生到距学校12千米的烈士陵园扫墓。一部分同学骑自行车先行，经时后，其余同学乘汽车出发，结果他们同时到达。已知汽车的速度是自行车速度的3倍，求汽车和自行车的速度。
四、拓展提高
1.在下渚湖里划船发现逆流划行400米的时间比顺流划行400米的时间多用了５分钟。已知水流速度为20米/分,求我们在静水中划船速度.
7.5 分式复习
一、知识回顾
1.下列各式：其中分式的个数有（ ）
(A) 1个 (B) 2个 (C) 3个 (D) 4个
2．当为任何实数时，下列分式中一定有意义的一个是 （ ）
(A) (B) (C) (D)
3.若分式的值为0，则的取值范围为 （ ）
(A) (B) (C) (D)
4.与分式的值相等的是 （ ）
(A) (B) (C) (D)
5.下列分式的运算中，正确的是 （ ）
(A) (B)
(C) (D)
6.本金，年利率，年后所得的本息和之间有如下的公式：.在这个公式中，已知那么（ ）
(A) (B) (C) (D)
二、课堂练习
1.不改变分式的值，使分式的分子、分母中各项系数都化为整数，= ____________
2.等式成立的条件是____________
3.已知分式，当时无意义，当时分式的值为0，则当时，分式的值为___________ 4.若方程无解，则的值为____________
5.计算：=____________ 6.已知，则____________
7.计算：= ___________ 8、在公式中，求出＝____________
解答题
1.计算：
(1) (3)
2．解方程：
(1) (2)
3. 先化简，再求值： 当时，求的值
三、拓展提高
1. 某一工程，在工程招标时，接到甲、乙两个工程队的投标书。施工一天，需付甲工程队工程款1.5万元, 乙工程队工程款1.1万元。工程领导小组根据甲、乙两队的投标书测算：
（1）甲队单独完成这项工程刚好如期完成；
（2）乙队单独完成这项工程要比规定日期多用5天；
（3）若甲、乙两队合做4天，余下的工程由乙队单独做也正好如期完成。
在不耽误工期的前提下，你觉得哪一种施工方案最节省工程款？
A
B
C
a
b
c
D
A
B
C
E
A
B
C
D
A
B
C
D
A
B
C
E
F
D
A
B
C
方法一
方法二
方法三
m
m
m
m
A
B
C
A
D
C
B
L1
L2
D
E
A
F
B
C
A
B
C
D
Ａ．
Ｂ．
Ｃ．
Ｄ．
Q
P
B
A
C
E
D
红
绿
蓝
红
红
蓝
闯关游戏规则
图10所示的面板上，有左右两组开头按钮.每组中的两个按钮均分别控制一个灯泡和一个发音装置.同时按下两组中各一个按钮：当两个灯泡都亮时闯关成功；当按错一个按钮时，发音装置就会发出“闯关失败”的声音.
1
2
1
2
图10
2
1
5
1
4
6
4
8
3
5
6
1
4
3
2
A
1
2
3
4
5
6
B