5.3 分式的乘除同步练习(含解析)
文档属性
| 名称 | 5.3 分式的乘除同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 936.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-22 00:00:00 | ||
图片预览



文档简介
初中数学浙教版七年级下册5.3 分式的乘除 同步练习
一、单选题
1.2x2-4÷1x2-2x 的计算结果为(?? )
A.?xx+2?????????????????????????????????B.?2xx+2?????????????????????????????????C.?2xx-2?????????????????????????????????D.?2x(x+2)
2.化简 x2-xx+1?x2-1x2-2x+1 的结果是(? )
A.?1x????????????????????????????????????????B.?x????????????????????????????????????????C.?x+1x-1????????????????????????????????????????D.?x-1x+1
3.计算 (-b2a)3 的结果是(?? )
A.?- b32a3???????????????????????????????????B.?- b36a3???????????????????????????????????C.?- b38a3???????????????????????????????????D.?b38a3
4.计算 (x3y2)2?xy3 ,得到的结果是(? )
A.?xy??????????????????????????????????????B.?x7y4??????????????????????????????????????C.?x7y??????????????????????????????????????D.?x5y6
5.化简 4x2x2-2x+1÷2xx+3-a 的结果为 2xx-1 ,则a=(?? )
A.?4???????????????????????????????????????????B.?3???????????????????????????????????????????C.?2???????????????????????????????????????????D.?1
6.代数式 x+2x-1 ÷ xx-1 有意义,则x的取值范围是(?? )
A.?x≠1??????????????????????????B.?x≠1且x≠0??????????????????????????C.?x≠﹣2且x≠1??????????????????????????D.?x≠﹣2且x≠0
7.若 ×xy=3x2y+2xy ,则 内应填的式子是(?? )
A.? 3x+2????????????????????????????????B.? x+2????????????????????????????????C.?3 xy+2????????????????????????????????D.? xy+2
8.一检测员在n分钟内可检查 a3 个产品,他在2小时内可检查产品(??? )个.
A.?2a3n???????????????????????????????????B.?40an???????????????????????????????????C.?a3n???????????????????????????????????D.?120an
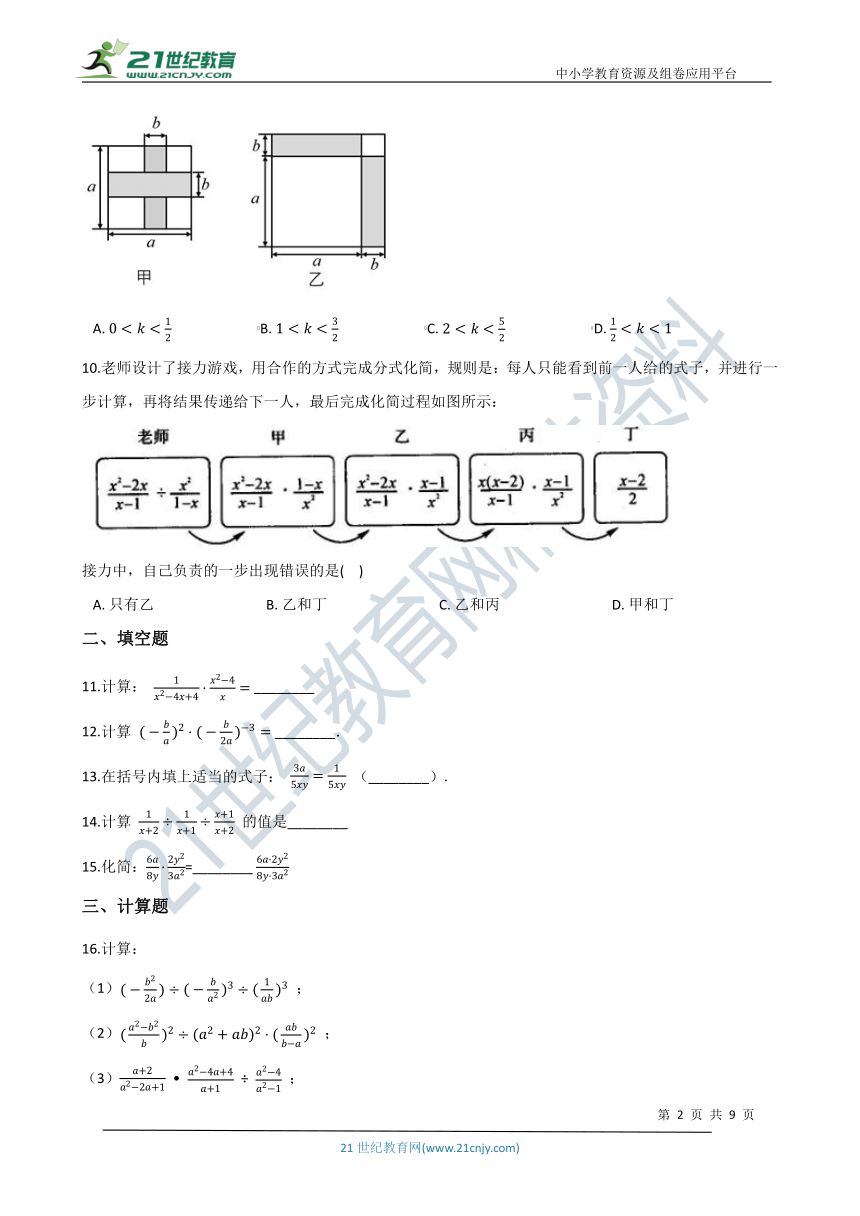
9.某小区有一块边长为 a 的正方形场地,规划修建两条宽为 b 的绿化带(如图中阴影部分所示).方案一如图甲所示,绿化带面积为 S甲 ;方案二如图乙所示,绿化带面积为 S乙 .设 k=S甲S乙(a>b>0) ,则 k 的取值范围为(??? )
A.?010.老师设计了接力游戏,用合作的方式完成分式化简,规则是:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成化简过程如图所示:
接力中,自己负责的一步出现错误的是( ??)
A.?只有乙????????????????????????????????B.?乙和丁????????????????????????????????C.?乙和丙????????????????????????????????D.?甲和丁
二、填空题
11.计算: 1x2-4x+4?x2-4x= ________
12.计算 (-ba)2?(-b2a)-3= ________.
13.在括号内填上适当的式子: 3a5xy=15xy (________).
14.计算 1x+2÷1x+1÷x+1x+2 的值是________
15.化简:6a8y·2y23a2=________?6a·2y28y·3a2
三、计算题
16.计算:
(1)(-b22a)÷(-ba2)3÷(1ab)3 ;
(2)(a2-b2b)2÷(a2+ab)2?(abb-a)2 ;
(3)a+2a2-2a+1 ? a2-4a+4a+1 ÷ a2-4a2-1 ;
(4)x2-1x2+2x+1÷2x2-24x2+8x+4÷(x-1)2 .
17.计算: x2+3xy-4y2x2+8xy+16y2÷x2+3x-3y-y2x2-16y2 .
18.计算 (-12a)÷(b2a)-2×3b2a2÷(-2a2b)3
答案解析部分
一、单选题
1. B
考点:分式的乘除法
解: 2x2-4÷1x2-2x
= 2(x+2)(x-2)÷1x(x-2)
= 2(x+2)(x-2)·x(x-2)
= 2xx+2 .
故答案为:B.
分析:先把分母因式分解,再把除法转换为乘法,约分化简得到结果.
2. B
考点:分式的乘除法
解:原式 =x(x-1)x+1?(x-1)(x+1)(x-1)2
=x
故答案为:B.
分析:先因式分解,再利用分式的约分计算即可。
3. C
考点:分式的乘除法
解:原式= -b3(2a)3=-b38a3 .
故答案为:C.
分析:根据分式的乘方,把分子分母分别乘方,据此计算即得.
4. C
考点:分式的乘除法
解:(x3y2)2· xy3
=x6y4· xy3
=x7y.
故答案为:C.
分析:利用积的乘方、幂的乘方,再利用分式的乘法计算即可。
5. A
考点:分式的乘除法
解: 2xx+3-a = 4x2(x-1)2 ÷ 2xx-1
= 4x2(x-1)2 ? x-12x
= 2xx-1 ,
∴3﹣a=﹣1,
∴a=4,
故答案为:A.
分析:根据除式=被除式除以商,再化简,根据题意可知2xx+3-a=2xx-1 , 就可得到关于a的方程,解方程求出a的值。
6. B
考点:分式的乘除法
解:由题意可得:
{x≠0x-1≠0 ,即x≠1且x≠0;
故答案为:B.
分析:要使代数式有意义,可知被除式的分母不等于0,除式的分子分母都不等于0,建立关于x的不等式组,然后求出不等式组的解集。
7. A
考点:分式的乘除法
解:根据题意得出 = 3x2y+2xyxy=3x+2
故答案为:A.
分析:根据题意得出 = 3x2y+2xyxy ,利用分式的性质求解即可.
8. B
考点:分式的乘除法
解:∵一检测员在n分钟内可检查 a3 个产品,
∴他在2小时内可检查产品: 120n × a3 = 40an (个).
故答案为:B.
分析:先求出检测员一分钟内可检查 a3n 个产品,然后乘以120分钟即可求出结论.
9. D
考点:列式表示数量关系,分式的乘除法
解:∵S甲=2ab-b2 , S乙=2ab.
k=s甲S乙=2ab-b22ab=1-b2a ,
∵a>b>0
∴ 12 <k<1
故答案为:D.
分析:由题意可求S甲=2ab-b2 , S乙=2ab,代入可求k的取值范围.
10. B
考点:分式的乘除法
解:原式=x2-2xx-1·1-xx2 , 故甲正确;
=x2-2xx-1·-x-1x2 , 故乙错误;
∵x2-2xx-1·x-1x2
=xx-2x-1·x-1x2 , 故丙正确;
=x-2x , 故丁错误;
∴接力中,自己负责的一步出现错误的乙和丁
故答案为:B
分析:先将分式除法转化为乘法运算,再将1-x转化为-(x-1),故乙错误;再将分子分母能分解因式的先分解因式,然后约分化简,可知丁错误,即可得出结果。
二、填空题
11. x+2x2-2x
考点:分式的乘除法
解: 1x2-4x+4?x2-4x
=1(x-2)2·(x-2)(x+2)x
=(x+2)x(x-2)
=x+2x2-2x
故答案为: x+2x2-2x.
分析:将各个分式的分子、分母能分解因式的分别分解因式,然后约分化为最简形式即可.
12. -8ab
考点:分式的乘除法,负整数指数幂的运算性质
解: (-ba)2?(-b2a)-3
= (-ba)2?(-2ab)3
= b2a2?(-8a3b3)
= -8ab .
故答案为: -8ab
分析:先把负指数幂转化为正指数幂,然后计算乘方,最后计算乘法即可求解.
13. 3a
考点:分式的乘除法
解:括号内的式子为 3a5xy÷15xy=3a5xy?5xy=3a ,
故答案为:3a.
分析:根据分式的除法法则计算即可,
14. 1
考点:分式的乘除法
解: 1x+2÷1x+1÷x+1x+2 ,
= 1x+2×(x+1)×x+2x+1
=1.
故答案为:1.
分析:将除法运算转化为乘法运算,再进行约分即可得到答案.
15.y2a
考点:分式的乘除法
解:原式=6a·2y28y·3a2=y2a ,
故答案为:y2a .
分析:根据整式的乘法法则进行计算即可,结果化成最简分式.
三、计算题
16. (1)解:原式=﹣ b22a ×(﹣ a6b3 )×a3b3= 12 a8b2
(2)解:原式= (a+b)2(a-b)2b2 ? 1a2(a+b)2 ? a2b2(a-b)2 =1
(3)解:原式= a+2(a-1)2 ? (a-2)2a+1 ? (a+1)(a-1)(a+2)(a-2) = a-2a-1
(4)解:原式= (x+1)(x-1)(x+1)2 ? 4(x+1)22(x+1)(x-1) ? 1(x-1)2 = 2(x-1)2
考点:分式的乘除法
分析:(1)原式利用除以一个数等于乘以这个数的倒数将除法运算化为乘法运算,约分即可得到结果;(2)原式先计算乘方运算,再利用除以一个数等于乘以这个数的倒数将除法运算化为乘法运算,约分即可得到结果;(3)原式利用除以一个数等于乘以这个数的倒数将除法运算化为乘法运算,约分即可得到结果;(4)原式先计算乘方运算,再利用除以一个数等于乘以这个数的倒数将除法运算化为乘法运算,约分即可得到结果.
17. 解:原式 =(x-y)(x+4y)(x+4y)2÷(x-y)(x+y+3)(x-4y)(x+4y)
=(x-y)(x+4y)(x+4y)2×((x-4y)(x+4y)(x-y)(x+y+3)
=x-4yx+y+3 .
考点:分式的乘除法
分析:先将分子与分母进行因式分解,再将除法转化为乘法,最后约分即可.
18. 解:原式= (-12a)÷4a2b2×3b2a2÷(-8a6b3)
= 12a×b24a2×3b2a2×18a6b3
= 3b64a11
考点:分式的乘除法,负整数指数幂的运算性质,积的乘方
分析:先计算负指数幂,积的乘方,再将除法乘法约分化简即可.
一、单选题
1.2x2-4÷1x2-2x 的计算结果为(?? )
A.?xx+2?????????????????????????????????B.?2xx+2?????????????????????????????????C.?2xx-2?????????????????????????????????D.?2x(x+2)
2.化简 x2-xx+1?x2-1x2-2x+1 的结果是(? )
A.?1x????????????????????????????????????????B.?x????????????????????????????????????????C.?x+1x-1????????????????????????????????????????D.?x-1x+1
3.计算 (-b2a)3 的结果是(?? )
A.?- b32a3???????????????????????????????????B.?- b36a3???????????????????????????????????C.?- b38a3???????????????????????????????????D.?b38a3
4.计算 (x3y2)2?xy3 ,得到的结果是(? )
A.?xy??????????????????????????????????????B.?x7y4??????????????????????????????????????C.?x7y??????????????????????????????????????D.?x5y6
5.化简 4x2x2-2x+1÷2xx+3-a 的结果为 2xx-1 ,则a=(?? )
A.?4???????????????????????????????????????????B.?3???????????????????????????????????????????C.?2???????????????????????????????????????????D.?1
6.代数式 x+2x-1 ÷ xx-1 有意义,则x的取值范围是(?? )
A.?x≠1??????????????????????????B.?x≠1且x≠0??????????????????????????C.?x≠﹣2且x≠1??????????????????????????D.?x≠﹣2且x≠0
7.若 ×xy=3x2y+2xy ,则 内应填的式子是(?? )
A.? 3x+2????????????????????????????????B.? x+2????????????????????????????????C.?3 xy+2????????????????????????????????D.? xy+2
8.一检测员在n分钟内可检查 a3 个产品,他在2小时内可检查产品(??? )个.
A.?2a3n???????????????????????????????????B.?40an???????????????????????????????????C.?a3n???????????????????????????????????D.?120an
9.某小区有一块边长为 a 的正方形场地,规划修建两条宽为 b 的绿化带(如图中阴影部分所示).方案一如图甲所示,绿化带面积为 S甲 ;方案二如图乙所示,绿化带面积为 S乙 .设 k=S甲S乙(a>b>0) ,则 k 的取值范围为(??? )
A.?0
接力中,自己负责的一步出现错误的是( ??)
A.?只有乙????????????????????????????????B.?乙和丁????????????????????????????????C.?乙和丙????????????????????????????????D.?甲和丁
二、填空题
11.计算: 1x2-4x+4?x2-4x= ________
12.计算 (-ba)2?(-b2a)-3= ________.
13.在括号内填上适当的式子: 3a5xy=15xy (________).
14.计算 1x+2÷1x+1÷x+1x+2 的值是________
15.化简:6a8y·2y23a2=________?6a·2y28y·3a2
三、计算题
16.计算:
(1)(-b22a)÷(-ba2)3÷(1ab)3 ;
(2)(a2-b2b)2÷(a2+ab)2?(abb-a)2 ;
(3)a+2a2-2a+1 ? a2-4a+4a+1 ÷ a2-4a2-1 ;
(4)x2-1x2+2x+1÷2x2-24x2+8x+4÷(x-1)2 .
17.计算: x2+3xy-4y2x2+8xy+16y2÷x2+3x-3y-y2x2-16y2 .
18.计算 (-12a)÷(b2a)-2×3b2a2÷(-2a2b)3
答案解析部分
一、单选题
1. B
考点:分式的乘除法
解: 2x2-4÷1x2-2x
= 2(x+2)(x-2)÷1x(x-2)
= 2(x+2)(x-2)·x(x-2)
= 2xx+2 .
故答案为:B.
分析:先把分母因式分解,再把除法转换为乘法,约分化简得到结果.
2. B
考点:分式的乘除法
解:原式 =x(x-1)x+1?(x-1)(x+1)(x-1)2
=x
故答案为:B.
分析:先因式分解,再利用分式的约分计算即可。
3. C
考点:分式的乘除法
解:原式= -b3(2a)3=-b38a3 .
故答案为:C.
分析:根据分式的乘方,把分子分母分别乘方,据此计算即得.
4. C
考点:分式的乘除法
解:(x3y2)2· xy3
=x6y4· xy3
=x7y.
故答案为:C.
分析:利用积的乘方、幂的乘方,再利用分式的乘法计算即可。
5. A
考点:分式的乘除法
解: 2xx+3-a = 4x2(x-1)2 ÷ 2xx-1
= 4x2(x-1)2 ? x-12x
= 2xx-1 ,
∴3﹣a=﹣1,
∴a=4,
故答案为:A.
分析:根据除式=被除式除以商,再化简,根据题意可知2xx+3-a=2xx-1 , 就可得到关于a的方程,解方程求出a的值。
6. B
考点:分式的乘除法
解:由题意可得:
{x≠0x-1≠0 ,即x≠1且x≠0;
故答案为:B.
分析:要使代数式有意义,可知被除式的分母不等于0,除式的分子分母都不等于0,建立关于x的不等式组,然后求出不等式组的解集。
7. A
考点:分式的乘除法
解:根据题意得出 = 3x2y+2xyxy=3x+2
故答案为:A.
分析:根据题意得出 = 3x2y+2xyxy ,利用分式的性质求解即可.
8. B
考点:分式的乘除法
解:∵一检测员在n分钟内可检查 a3 个产品,
∴他在2小时内可检查产品: 120n × a3 = 40an (个).
故答案为:B.
分析:先求出检测员一分钟内可检查 a3n 个产品,然后乘以120分钟即可求出结论.
9. D
考点:列式表示数量关系,分式的乘除法
解:∵S甲=2ab-b2 , S乙=2ab.
k=s甲S乙=2ab-b22ab=1-b2a ,
∵a>b>0
∴ 12 <k<1
故答案为:D.
分析:由题意可求S甲=2ab-b2 , S乙=2ab,代入可求k的取值范围.
10. B
考点:分式的乘除法
解:原式=x2-2xx-1·1-xx2 , 故甲正确;
=x2-2xx-1·-x-1x2 , 故乙错误;
∵x2-2xx-1·x-1x2
=xx-2x-1·x-1x2 , 故丙正确;
=x-2x , 故丁错误;
∴接力中,自己负责的一步出现错误的乙和丁
故答案为:B
分析:先将分式除法转化为乘法运算,再将1-x转化为-(x-1),故乙错误;再将分子分母能分解因式的先分解因式,然后约分化简,可知丁错误,即可得出结果。
二、填空题
11. x+2x2-2x
考点:分式的乘除法
解: 1x2-4x+4?x2-4x
=1(x-2)2·(x-2)(x+2)x
=(x+2)x(x-2)
=x+2x2-2x
故答案为: x+2x2-2x.
分析:将各个分式的分子、分母能分解因式的分别分解因式,然后约分化为最简形式即可.
12. -8ab
考点:分式的乘除法,负整数指数幂的运算性质
解: (-ba)2?(-b2a)-3
= (-ba)2?(-2ab)3
= b2a2?(-8a3b3)
= -8ab .
故答案为: -8ab
分析:先把负指数幂转化为正指数幂,然后计算乘方,最后计算乘法即可求解.
13. 3a
考点:分式的乘除法
解:括号内的式子为 3a5xy÷15xy=3a5xy?5xy=3a ,
故答案为:3a.
分析:根据分式的除法法则计算即可,
14. 1
考点:分式的乘除法
解: 1x+2÷1x+1÷x+1x+2 ,
= 1x+2×(x+1)×x+2x+1
=1.
故答案为:1.
分析:将除法运算转化为乘法运算,再进行约分即可得到答案.
15.y2a
考点:分式的乘除法
解:原式=6a·2y28y·3a2=y2a ,
故答案为:y2a .
分析:根据整式的乘法法则进行计算即可,结果化成最简分式.
三、计算题
16. (1)解:原式=﹣ b22a ×(﹣ a6b3 )×a3b3= 12 a8b2
(2)解:原式= (a+b)2(a-b)2b2 ? 1a2(a+b)2 ? a2b2(a-b)2 =1
(3)解:原式= a+2(a-1)2 ? (a-2)2a+1 ? (a+1)(a-1)(a+2)(a-2) = a-2a-1
(4)解:原式= (x+1)(x-1)(x+1)2 ? 4(x+1)22(x+1)(x-1) ? 1(x-1)2 = 2(x-1)2
考点:分式的乘除法
分析:(1)原式利用除以一个数等于乘以这个数的倒数将除法运算化为乘法运算,约分即可得到结果;(2)原式先计算乘方运算,再利用除以一个数等于乘以这个数的倒数将除法运算化为乘法运算,约分即可得到结果;(3)原式利用除以一个数等于乘以这个数的倒数将除法运算化为乘法运算,约分即可得到结果;(4)原式先计算乘方运算,再利用除以一个数等于乘以这个数的倒数将除法运算化为乘法运算,约分即可得到结果.
17. 解:原式 =(x-y)(x+4y)(x+4y)2÷(x-y)(x+y+3)(x-4y)(x+4y)
=(x-y)(x+4y)(x+4y)2×((x-4y)(x+4y)(x-y)(x+y+3)
=x-4yx+y+3 .
考点:分式的乘除法
分析:先将分子与分母进行因式分解,再将除法转化为乘法,最后约分即可.
18. 解:原式= (-12a)÷4a2b2×3b2a2÷(-8a6b3)
= 12a×b24a2×3b2a2×18a6b3
= 3b64a11
考点:分式的乘除法,负整数指数幂的运算性质,积的乘方
分析:先计算负指数幂,积的乘方,再将除法乘法约分化简即可.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
