5.5.2分式方程的应用 同步练习(含解析)
文档属性
| 名称 | 5.5.2分式方程的应用 同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 919.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-21 00:00:00 | ||
图片预览




文档简介
初中数学浙教版七年级下册5.5.2分式方程的应用 同步练习
一、单选题
1.为祝福祖国70周年华诞,兴义市中等职业学校全体师生开展了以“我和我的祖国、牢记初心和使命”为主题的演讲比赛,为奖励获奖学生,学校购买了一些钢笔和毛笔,钢笔单价是毛笔单价的1.5倍,购买钢笔用了1200元,购买毛笔用了1500元,购买的钢笔数比毛笔少35支,钢笔、毛笔的单价分别是多少元?如果设毛笔的单价为x元/支,那么下面所列方程正确的是(?? )
A.?12001.5x-1500x=35????????????????????????????????????????????B.?1500x-12001.5x=35
C.?1500x=35-12001.5x???????????????????????????????????????????D.?1200x-15001.5x=35
2.某工厂生产空气净化器,实际平均每天比原计划多生产100 台空气净化器,生产1200 台空气净化器的时间与原计划生产900 台空气净化器所需时间相同.若设原计划每天生产x 台空气净化器,则根据题意可列方程为(?? )
A.?1200x+100=900x??????????B.?1200x-100=900x=0??????????C.?900x+100=1200x??????????D.?1200x-9000x=10
3.A、B两地相距 36 千米,一艘轮船从A地顺流行至B地,又立即从B地逆流返回A地,共用9小时,已知水流速度为 4 千米/时,若设该轮船在静水中的速度为x千米/时,则可列方程为(?? )
A.? 36 x+4+36x-4=9????????????????B.?364+x+364-x=9????????????????C.? 36x+4=9????????????????D.?36x+4-36x-4=9
4.2020年5月1日,北京市正式实施《北京市生活垃圾管理条例》,生活垃圾按照厨余垃圾,可回收物,有害垃圾,其他垃圾进行分类.小红所住小区5月和12月的厨余垃圾分出量和其他三种垃圾的总量的相关信息如下表所示:
类别???????????????????? 月份
5 月
12 月
厨余垃圾分出量(千克)
660
8400
其他三种垃圾的总量(千克)
x
710x
厨余垃圾分出量如果厨余垃圾分出率 = 厨余垃圾分出量生活垃圾总量×100% (生活垃圾总量 = 厨余垃圾分出量 + 其他三种垃圾的总量),且该小区 12 月的厨余垃圾分出率约是 5 月的厨余垃圾分出率的 14 倍,那么下面列式正确的是(? )
A.?660x×14=8400710x??????????????????????????????????????????????B.?660660+x×14=84008400+710x
C.?660660+x×14=84008400+710x×14??????????????????????????D.?660+x660×14=8400+710x8400
5.小明和同学去距学校15千米的某景点参观,小明骑自行车先走,过了10分钟,其余同学乘汽车出发,结果他们同时到达,已知汽车的速度比小明骑车速度快50千米/时.设小明骑车速度为 x 千米/时,则所列方程正确的是(?? ).
A.?15x-50-15x=10???????????B.?15x-15x+50=10???????????C.?15x-15x-50=16???????????D.?15x-15x+50=16
6.精元电子厂准备生产5400套电子元件,甲车间独立生产一半后,由于要尽快投入市场,乙车间也加入了该电子元件的生产,若乙车间每天生产的电子元件套数是甲车间的1.5倍,结果用30天完成任务,问甲车间每天生产电子元件多少套?在这个问题中设甲车间每天生产电子元件x套,根据题意可得方程为(?? )
A.?2700x+27001.5x=30????????????????????????????????????????????B.?2700x+2700x+1.5x=30
C.?2700x+5400x+1.5x=30?????????????????????????????????????????D.?5400x+2700x+1.5x=30
7.一个容器盛满酒精,第一次倒出10升后,用水加满,第二次倒出6升后,再用水加满,这时容器内的酒精与水的体积之比为7:13,则这个容器的容积为(?? )
A.?18升????????????????????????????????????B.?20升????????????????????????????????????C.?24升????????????????????????????????????D.?30升
8.某市铺设一条长660米的管道,为了尽量减少施工对城市交通造成的影响,实际施工时每天铺设的管道长比计划增加10%,结果提前6天完工,求实际每天铺设管道长度及实际施工天数,小明列出方程: 660x-660x(1+10%) =6,题中x表示的量为(??? )
A.?实际每天铺设管道长度????????B.?实际施工天数????????C.?计划施工天数????????D.?计划每天铺设管道的长度
9.2020年新冠肺炎疫情影响全球,某企业临时增加甲、乙两个厂房生产口罩,甲厂房每天生产的数量是乙厂房每天生产数量的2倍,两厂房各加工6000箱口罩,甲厂房比乙厂房少用5天.则甲、乙两厂房每天各生产的口罩箱数为(??? )
A.?1200,600???????????????????????B.?600,1200???????????????????????C.?1600,800???????????????????????D.?800,1600
10.一项工程需在规定日期完成,如果甲队单独做,就要超过规定日期1天,如果乙队单独做,要超过规定日期4天.现在先由甲、乙两队一起做3天,剩下的工程由乙队单独做,刚好在规定日期完成,则规定日期为(???? )
A.?6天?????????????????????????????????????B.?8天?????????????????????????????????????C.?10天?????????????????????????????????????D.?7.5天
二、填空题
11.甲、乙两同学的家与学校的距离均为3000米,甲同学先步行600米然后乘公交车去学校,乙同学骑自行车去学校,已知甲步行的速度是乙骑自行车速度的 12 ,公交车速度是乙骑自行车速度的2倍.甲乙两同学同时从家出发去学校结果甲同学比乙同学早到2分钟,若甲同学到达学校时,乙同学离学校还有m米,则 m= ________.
12.A、B两地相距121千米,甲车和乙车的平均速度之比为4:5,两车同时从A地出发到B地,乙车比甲车早到20分钟,求甲车的平均速度.若设甲车平均速度为4x千米/小时,则所列方程是________.
13.某校为了丰富学生的校园生活,准备购买一批陶笛.已知A型陶笛比B型陶笛的单价低20元,用2700元购买A型陶笛与用4500元购买B型陶笛的数量相同,设A型陶笛的单价为 x 元,根据题意列出正确的方程是________.
14.某危险品工厂采用甲型、乙型两种机器人代替人力搬运产品.甲型机器人比乙型机器人每小时多搬运 10kg ,甲型机器人搬运 800kg 所用时间与乙型机器人搬运 600kg 所用时间相等.问乙型机器人每小时搬运多少 kg 产品?
根据以上信息,解答下列问题.
(1)小华同学设乙型机器人每小时搬运 xkg 产品,可列方程为________小惠同学设甲型机器人搬运 800kg 所用时间为 y 小时,可列方程为________.
(2)乙型机器人每小时搬运产品________ kg .
三、解答题
15.长方形的面积是 390m2 ,如果将长延长至原来的2倍,且长方形面积保持不变,那么宽会比原来少 13m ,求原来长方形的长.
16.多多果品店在批发市场购买某种水果销售,第一次用1200元购进若干千克,由于水果畅销,很快售完,第二次用1430元购买了一批水果,每千克的进价比第一次提高了 10% ,所购买的水果的数量比第一次多20千克,求第一次购买水果的进价是每千克多少元?
17.南浔区某校组织同学乘大巴车前往“研学旅行”基地开展爱国教育活动,基地离学校有120千米,队伍乘大巴车8:00从学校出发.苏老师因有事情,8:30从学校自驾小汽车以大巴车1.5倍的速度追赶,追上大巴车后继续前行,结果比队伍提前10分钟到达基地.问:
(1)设大巴午的平均速度是x(km/h),利用速度、时间和路程之间的关系填写下表.(要求:填上适当的代数式,完成表格)(温馨提示:请填写在答题卷相对应的表格内)
速度(km/h)
路程(km)
时间(h)
大巴车
x
120
________
小汽车
________
120
________
(2)列出方程,并求出大巴车与小汽车的平均速度.
(3)当苏老师追上大巴车时,大巴车离基地还有多远?
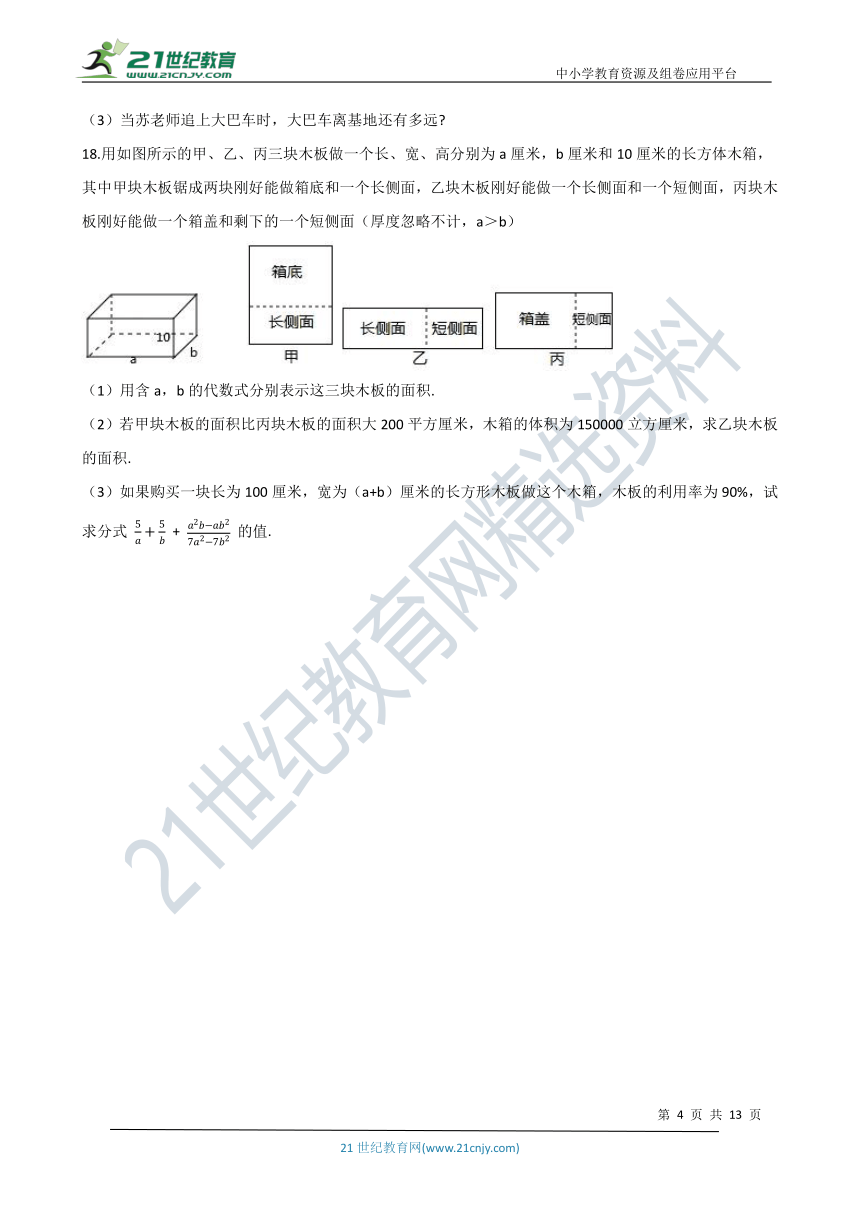
18.用如图所示的甲、乙、丙三块木板做一个长、宽、高分别为a厘米,b厘米和10厘米的长方体木箱,其中甲块木板锯成两块刚好能做箱底和一个长侧面,乙块木板刚好能做一个长侧面和一个短侧面,丙块木板刚好能做一个箱盖和剩下的一个短侧面(厚度忽略不计,a>b)
(1)用含a,b的代数式分别表示这三块木板的面积.
(2)若甲块木板的面积比丙块木板的面积大200平方厘米,木箱的体积为150000立方厘米,求乙块木板的面积.
(3)如果购买一块长为100厘米,宽为(a+b)厘米的长方形木板做这个木箱,木板的利用率为90%,试求分式 5a+5b + a2b-ab27a2-7b2 的值.
答案解析部分
一、单选题
1. B
考点:分式方程的实际应用
解:设毛笔单价x元/支,由题意得: 1500x-12001.5x=35 ,
故答案为:B.
分析:根据题意可得:1500元购买的毛笔数量-1200元购买的钢笔数量=20支,根据等量关系列出方程即可.
2. A
考点:分式方程的实际应用
解:设原计划每天生产x 台空气净化器,根据题意得
120x+100=900x.
故答案为:A.
分析:此题的等量关系为:1200÷实际工作效率=900÷原计划的工作效率,列方程即可。
3. A
考点:分式方程的实际应用
解:设该轮船在静水中的速度为x千米/时,列方程得
36 x+4+36x-4=9 .
故答案为:A.
分析:设该轮船在静水中的速度为x千米/时,可得顺流速度为(x+4)千米/时,逆流速度为(x-4)千米/时,根据顺流时间+逆流时间=9小时,列出方程即可.
4. B
考点:列分式方程
解:5月份厨余垃圾分出率= 660660+x ,12月份厨余垃圾分出率= 84008400+710x ,
∴由题意得 660660+x×14=84008400+710x ,
故答案为:B.
分析:根据?“厨余垃圾分出率?=?厨余垃圾分出量生活垃圾总量×100%?”和“ 该小区?12?月的厨余垃圾分出率约是?5?月的厨余垃圾分出率的?14?倍 ”列出方程即可。
5. D
考点:分式方程的实际应用
解:10分钟= 16 小时
设小明骑车速度为 x 千米/时,则汽车的速度为(x+50)千米/时,
根据题意可得: 15x-15x+50=16
故答案为:D.
分析:设小明骑车速度为 x 千米/时,则汽车的速度为(x+50)千米/时,根据“骑车同学走完全程所用的时间=坐汽车同学走完全程所用的时间”可以列出相应的方程,从而可以得到哪个选项是正确的.
6. B
考点:分式方程的实际应用
解:首先设甲车间每天能生产x个,则乙车间每天能生产1.5x个,由题意可得等量关系:甲车间生产2700件所用的时间+甲乙两车间生产2700件所用的时间=30天,根据等量关系可列出方程 2700x+2700x+1.5x=30 .
故答案为:B.
分析:先设甲车间每天能生产x个,则乙车间每天能生产1.5x个,根据“甲车间生产2700件所用的时间+甲乙两车间生产2700件所用的时间=30天”列出方程即可.
7. B
考点:分式方程的实际应用
解:设这个容器的容积为x升,
由题意得:x﹣10﹣6× x-10x = 77+13 x,
整理得:13x2﹣320x+1200=0,
解得:x=20,或x= 6013 (舍去),
∴x=20,
经检验,x=20是原分式方程的解;
即这个容器的容积为20升;
故答案为:B.
分析:设这个容器的容积为x升,由容器中剩余酒精的量的不同表示方法列出分式方程,然后解分式方程,再检验即可.
8. D
考点:分式方程的实际应用
解:设原计划每天铺设管道 x 米,则实际每天铺设管道 (1+10%)x ,
根据题意,可列方程: 660x-660x(1+10%)=6 ,
所以小明所列方程中未知数 x 所表示的量是计划每天铺设管道的长度,
故答案为:D.
分析:根据计划所用时间-实际所用时间=6,可知方程中未知数x所表示的量.
9. A
考点:分式方程的实际应用
解:设乙厂房每天生产x箱口罩,则甲厂房每天生产2x箱口罩,
依题意得: 6000x-60002x=5 ,
解得:x=600,
经检验,x=600是原分式方程的解,且符合题意,
∴2x=1200.
故答案选:A .
分析:先设乙厂房每天生产x箱口罩,则甲厂房每天生产2x箱口罩,根据工作时间=工作总量÷工作效率且两厂房各加工6000箱口罩时甲厂房比乙厂房少用5天,可得出关于x的分式方程,解方程即可得出结论.
10. B
考点:分式方程的实际应用
解:设工作总量为1,规定日期为x天,则若单独做,甲队需(x+1)天,乙队需(x+4)天,根据题意列方程得
3( 1x+1+1x+4 )+ x-3x+4 =1,
解方程可得x=8,
经检验x=8是分式方程的解,
故答案为:B.
分析:先设规定日期为x,再用x表示出甲、乙的工作效率,最后利用工作总量列出方程即可。
二、填空题
11. 600
考点:分式方程的实际应用
解:设乙骑自行车的速度为x米/分钟,则甲步行速度是 12 x米/分钟,公交车的速度是2x米/分钟,
根据题意得
60012x+3000-6002x=3000x-2 ?,
解得:x=300米/分钟,
经检验x=300是方程的根,
则乙骑自行车的速度为300米/分钟.
那么甲同学到达学校时,乙同学离学校还=2×300=600米.
故答案为:600.
分析:设乙骑自行车的速度为x米/分钟,则甲步行速度是 12 x米/分钟,公交车的速度是2x米/分钟,根据题意找到等量关系:甲步行的时间+甲公车时间=乙的时间-2分钟,列方程即可得到乙的速度,甲同学到达学校时,乙同学离学校还有2x米,即可得到结论;
12. 1214x-1215x=13
考点:分式方程的实际应用
解:设甲车平均速度为4x千米/小时,则乙车平均速度为5x千米/小时,根据题意得:
1214x-1215x=13.
故答案为: 1214x-1215x=13.
分析:设甲车平均速度为4x千米/小时,则乙车平均速度为5x千米/小时,根据“ 两车同时从A地出发到B地,乙车比甲车早到20分钟 ”列出方程即可.
13. 2700x=4500x+20
考点:列分式方程
解:设A型陶笛的单价为x元,则B型陶笛的单价为(x+20)元,根据用2700元购买A型陶笛与用4500元购买B型陶笛的数量相同,可得 2700x=4500x+20 .
故答案为: 2700x=4500x+20 .
分析:设A型陶笛的单价为x元,则B型陶笛的单价为(x+20)元,根据“根据用2700元购买A型陶笛与用4500元购买B型陶笛的数量相同”列出方程即可。
14. (1)800x+10=600x;800y=600y+10
(2)30
考点:解分式方程,列分式方程
解:(1)设乙型机器人每小时搬运 xkg 产品,则甲型机器人每小时搬运(x+10)kg,由题意得
800x+10=600x ,
设甲型机器人搬运 800kg 所用时间为 y 小时,由题意得
800y=600y+10 ,
故答案为: 800x+10=600x , 800y=600y+10 ;
(2)设乙型机器人每小时搬运 xkg 产品,则甲型机器人每小时搬运(x+10)kg,由题意得
800x+10=600x ,
解得x=30,
经检验,x=30是方程的解,
答:乙型机器人每小时搬运产品30kg.
故答案为:30.
分析:(1)设乙型机器人每小时搬运 xkg 产品,根据甲型机器人搬运 800kg 所用时间与乙型机器人搬运 600kg 所用时间相等列方程;设甲型机器人搬运 800kg 所用时间为 y 小时,根据甲型机器人比乙型机器人每小时多搬运 10kg 列方程;(2)设乙型机器人每小时搬运 xkg 产品,则甲型机器人每小时搬运(x+10)kg,由题意得 800x+10=600x ,解方程即可.
三、解答题
15. 解:设原来长方形的长是x厘米,则新长方形的长是 2x 厘米.
390x-3902x=13
解得 x=15
经检验, x=15 是原方程的解,且符合题意.
答:原长方形的长是15厘米.
考点:分式方程的实际应用
分析:设原来长方形的长是x厘米,则新长方形的长是 2x 厘米,根据原长方形的宽-新长方形的宽=13m,列出方程,解之并检验即可.
16. 解:设第一次购买水果的进价是每千克 x 元,
依题意得: 1200x=1430x(1+20%)-20 ,
解之得: x=5 ,
经检验, x=5 是原方程的解并符合题意,
所以,原方程的解是 x=5 .
答:第一次购买水果的进价是每千克5元.
考点:分式方程的实际应用
分析:设第一次购买水果的进价是每千克 x 元,根据第二次购买的水果的数量比第一次多20千克列方程求解即可.
17. (1)1.5x;120x;1201.5x
(2)解:设大巴的平均速度为x公里/小时,则小车的平均速度为1.5x公里/小时,
根据题意,得: 120x=12+1201.5x+16
解得:x=60,
经检验:x=60是原方程的解,
答:大巴的平均速度为60公里/小时,则小车的平均速度为90公里/小时;
(3)解:设苏老师赶上大巴的地点到基地的路程有y公里,
根据题意,得: 120-y60=120-y90+12
解得:y=30,
答:苏老师追上大巴车的地点到基地的路程有30公里.
考点:解分式方程,分式方程的实际应用
解:(1)
?
速度(km/h)
路程(km)
时间(h)
大巴车
x
120
120x
小汽车
1.5x
120
1201.5x
分析:(1)根据小汽车的速度=大巴车的速度×1.5,用含x的代数式表示出小汽车的速度;再利用时间=路程÷速度,分别用含x的代数式表示出两车的时间。
(2)抓住关键语句: 队伍乘大巴车8:00从学校出发;苏老师8:30从学校自驾小汽车出发,结果比队伍提前10分钟到达基地.; 此题的等量关系为:大巴车行驶120千米的路程所用的时间=小汽车行驶120千米的时间+12+16 , 设未知数列方程,再解方程检验,即可求解。
(3)抓住已知条件:苏老师自驾小汽车追上大巴车后继续前行,结果比队伍提前10分钟到达基地.,据此设未知数,列方程求解即可。
18. (1)解:由图可得:甲块木板的面积:(ab+10a)平方厘米;乙块木板的面积:(10a+10b)平方厘米;丙块木板的面积:(ab+10b)平方厘米;
(2)解:由题意可得: {ab+10a-(ab+10b)=20010ab=150000 ,
即 {a-b=20ab=15000 ,
则(a+b)2=(a﹣b)2+4ab=400+60000=60400,
则乙块木板的面积为10a+10b=10(a+b)=10 60400 =200 151 (cm2);
(3)解:由题意可得: ab+10a+10a+10b+ab+10b100(a+b) =90%,
化简得ab=35(a+b),
则 5a + 5b + a2b-ab27a2-7b2
= 5(a+b)ab + ab(a-b)7(a+b)(a-b)
= 5(a+b)ab + ab7(a+b)
= 5(a+b)35(a+b) + 35(a+b)7(a+b)
= 17 +5
= 367 .
考点:分式方程的实际应用,二元一次方程组的应用-几何问题
分析:(1)利用展开图,结合立体图形的边长即可得出答案;
(2)利用“甲块木板的面积比丙块木板的面积大200平方厘米,木箱的体积为150000立方厘米”,结合(1)中所求得出等式即可求解;
(3)利用(1)中所求表示出箱子的侧面积以及木板的利用率为90%,得出等式求出ab=35(a+b),再代入计算即可求解.
一、单选题
1.为祝福祖国70周年华诞,兴义市中等职业学校全体师生开展了以“我和我的祖国、牢记初心和使命”为主题的演讲比赛,为奖励获奖学生,学校购买了一些钢笔和毛笔,钢笔单价是毛笔单价的1.5倍,购买钢笔用了1200元,购买毛笔用了1500元,购买的钢笔数比毛笔少35支,钢笔、毛笔的单价分别是多少元?如果设毛笔的单价为x元/支,那么下面所列方程正确的是(?? )
A.?12001.5x-1500x=35????????????????????????????????????????????B.?1500x-12001.5x=35
C.?1500x=35-12001.5x???????????????????????????????????????????D.?1200x-15001.5x=35
2.某工厂生产空气净化器,实际平均每天比原计划多生产100 台空气净化器,生产1200 台空气净化器的时间与原计划生产900 台空气净化器所需时间相同.若设原计划每天生产x 台空气净化器,则根据题意可列方程为(?? )
A.?1200x+100=900x??????????B.?1200x-100=900x=0??????????C.?900x+100=1200x??????????D.?1200x-9000x=10
3.A、B两地相距 36 千米,一艘轮船从A地顺流行至B地,又立即从B地逆流返回A地,共用9小时,已知水流速度为 4 千米/时,若设该轮船在静水中的速度为x千米/时,则可列方程为(?? )
A.? 36 x+4+36x-4=9????????????????B.?364+x+364-x=9????????????????C.? 36x+4=9????????????????D.?36x+4-36x-4=9
4.2020年5月1日,北京市正式实施《北京市生活垃圾管理条例》,生活垃圾按照厨余垃圾,可回收物,有害垃圾,其他垃圾进行分类.小红所住小区5月和12月的厨余垃圾分出量和其他三种垃圾的总量的相关信息如下表所示:
类别???????????????????? 月份
5 月
12 月
厨余垃圾分出量(千克)
660
8400
其他三种垃圾的总量(千克)
x
710x
厨余垃圾分出量如果厨余垃圾分出率 = 厨余垃圾分出量生活垃圾总量×100% (生活垃圾总量 = 厨余垃圾分出量 + 其他三种垃圾的总量),且该小区 12 月的厨余垃圾分出率约是 5 月的厨余垃圾分出率的 14 倍,那么下面列式正确的是(? )
A.?660x×14=8400710x??????????????????????????????????????????????B.?660660+x×14=84008400+710x
C.?660660+x×14=84008400+710x×14??????????????????????????D.?660+x660×14=8400+710x8400
5.小明和同学去距学校15千米的某景点参观,小明骑自行车先走,过了10分钟,其余同学乘汽车出发,结果他们同时到达,已知汽车的速度比小明骑车速度快50千米/时.设小明骑车速度为 x 千米/时,则所列方程正确的是(?? ).
A.?15x-50-15x=10???????????B.?15x-15x+50=10???????????C.?15x-15x-50=16???????????D.?15x-15x+50=16
6.精元电子厂准备生产5400套电子元件,甲车间独立生产一半后,由于要尽快投入市场,乙车间也加入了该电子元件的生产,若乙车间每天生产的电子元件套数是甲车间的1.5倍,结果用30天完成任务,问甲车间每天生产电子元件多少套?在这个问题中设甲车间每天生产电子元件x套,根据题意可得方程为(?? )
A.?2700x+27001.5x=30????????????????????????????????????????????B.?2700x+2700x+1.5x=30
C.?2700x+5400x+1.5x=30?????????????????????????????????????????D.?5400x+2700x+1.5x=30
7.一个容器盛满酒精,第一次倒出10升后,用水加满,第二次倒出6升后,再用水加满,这时容器内的酒精与水的体积之比为7:13,则这个容器的容积为(?? )
A.?18升????????????????????????????????????B.?20升????????????????????????????????????C.?24升????????????????????????????????????D.?30升
8.某市铺设一条长660米的管道,为了尽量减少施工对城市交通造成的影响,实际施工时每天铺设的管道长比计划增加10%,结果提前6天完工,求实际每天铺设管道长度及实际施工天数,小明列出方程: 660x-660x(1+10%) =6,题中x表示的量为(??? )
A.?实际每天铺设管道长度????????B.?实际施工天数????????C.?计划施工天数????????D.?计划每天铺设管道的长度
9.2020年新冠肺炎疫情影响全球,某企业临时增加甲、乙两个厂房生产口罩,甲厂房每天生产的数量是乙厂房每天生产数量的2倍,两厂房各加工6000箱口罩,甲厂房比乙厂房少用5天.则甲、乙两厂房每天各生产的口罩箱数为(??? )
A.?1200,600???????????????????????B.?600,1200???????????????????????C.?1600,800???????????????????????D.?800,1600
10.一项工程需在规定日期完成,如果甲队单独做,就要超过规定日期1天,如果乙队单独做,要超过规定日期4天.现在先由甲、乙两队一起做3天,剩下的工程由乙队单独做,刚好在规定日期完成,则规定日期为(???? )
A.?6天?????????????????????????????????????B.?8天?????????????????????????????????????C.?10天?????????????????????????????????????D.?7.5天
二、填空题
11.甲、乙两同学的家与学校的距离均为3000米,甲同学先步行600米然后乘公交车去学校,乙同学骑自行车去学校,已知甲步行的速度是乙骑自行车速度的 12 ,公交车速度是乙骑自行车速度的2倍.甲乙两同学同时从家出发去学校结果甲同学比乙同学早到2分钟,若甲同学到达学校时,乙同学离学校还有m米,则 m= ________.
12.A、B两地相距121千米,甲车和乙车的平均速度之比为4:5,两车同时从A地出发到B地,乙车比甲车早到20分钟,求甲车的平均速度.若设甲车平均速度为4x千米/小时,则所列方程是________.
13.某校为了丰富学生的校园生活,准备购买一批陶笛.已知A型陶笛比B型陶笛的单价低20元,用2700元购买A型陶笛与用4500元购买B型陶笛的数量相同,设A型陶笛的单价为 x 元,根据题意列出正确的方程是________.
14.某危险品工厂采用甲型、乙型两种机器人代替人力搬运产品.甲型机器人比乙型机器人每小时多搬运 10kg ,甲型机器人搬运 800kg 所用时间与乙型机器人搬运 600kg 所用时间相等.问乙型机器人每小时搬运多少 kg 产品?
根据以上信息,解答下列问题.
(1)小华同学设乙型机器人每小时搬运 xkg 产品,可列方程为________小惠同学设甲型机器人搬运 800kg 所用时间为 y 小时,可列方程为________.
(2)乙型机器人每小时搬运产品________ kg .
三、解答题
15.长方形的面积是 390m2 ,如果将长延长至原来的2倍,且长方形面积保持不变,那么宽会比原来少 13m ,求原来长方形的长.
16.多多果品店在批发市场购买某种水果销售,第一次用1200元购进若干千克,由于水果畅销,很快售完,第二次用1430元购买了一批水果,每千克的进价比第一次提高了 10% ,所购买的水果的数量比第一次多20千克,求第一次购买水果的进价是每千克多少元?
17.南浔区某校组织同学乘大巴车前往“研学旅行”基地开展爱国教育活动,基地离学校有120千米,队伍乘大巴车8:00从学校出发.苏老师因有事情,8:30从学校自驾小汽车以大巴车1.5倍的速度追赶,追上大巴车后继续前行,结果比队伍提前10分钟到达基地.问:
(1)设大巴午的平均速度是x(km/h),利用速度、时间和路程之间的关系填写下表.(要求:填上适当的代数式,完成表格)(温馨提示:请填写在答题卷相对应的表格内)
速度(km/h)
路程(km)
时间(h)
大巴车
x
120
________
小汽车
________
120
________
(2)列出方程,并求出大巴车与小汽车的平均速度.
(3)当苏老师追上大巴车时,大巴车离基地还有多远?
18.用如图所示的甲、乙、丙三块木板做一个长、宽、高分别为a厘米,b厘米和10厘米的长方体木箱,其中甲块木板锯成两块刚好能做箱底和一个长侧面,乙块木板刚好能做一个长侧面和一个短侧面,丙块木板刚好能做一个箱盖和剩下的一个短侧面(厚度忽略不计,a>b)
(1)用含a,b的代数式分别表示这三块木板的面积.
(2)若甲块木板的面积比丙块木板的面积大200平方厘米,木箱的体积为150000立方厘米,求乙块木板的面积.
(3)如果购买一块长为100厘米,宽为(a+b)厘米的长方形木板做这个木箱,木板的利用率为90%,试求分式 5a+5b + a2b-ab27a2-7b2 的值.
答案解析部分
一、单选题
1. B
考点:分式方程的实际应用
解:设毛笔单价x元/支,由题意得: 1500x-12001.5x=35 ,
故答案为:B.
分析:根据题意可得:1500元购买的毛笔数量-1200元购买的钢笔数量=20支,根据等量关系列出方程即可.
2. A
考点:分式方程的实际应用
解:设原计划每天生产x 台空气净化器,根据题意得
120x+100=900x.
故答案为:A.
分析:此题的等量关系为:1200÷实际工作效率=900÷原计划的工作效率,列方程即可。
3. A
考点:分式方程的实际应用
解:设该轮船在静水中的速度为x千米/时,列方程得
36 x+4+36x-4=9 .
故答案为:A.
分析:设该轮船在静水中的速度为x千米/时,可得顺流速度为(x+4)千米/时,逆流速度为(x-4)千米/时,根据顺流时间+逆流时间=9小时,列出方程即可.
4. B
考点:列分式方程
解:5月份厨余垃圾分出率= 660660+x ,12月份厨余垃圾分出率= 84008400+710x ,
∴由题意得 660660+x×14=84008400+710x ,
故答案为:B.
分析:根据?“厨余垃圾分出率?=?厨余垃圾分出量生活垃圾总量×100%?”和“ 该小区?12?月的厨余垃圾分出率约是?5?月的厨余垃圾分出率的?14?倍 ”列出方程即可。
5. D
考点:分式方程的实际应用
解:10分钟= 16 小时
设小明骑车速度为 x 千米/时,则汽车的速度为(x+50)千米/时,
根据题意可得: 15x-15x+50=16
故答案为:D.
分析:设小明骑车速度为 x 千米/时,则汽车的速度为(x+50)千米/时,根据“骑车同学走完全程所用的时间=坐汽车同学走完全程所用的时间”可以列出相应的方程,从而可以得到哪个选项是正确的.
6. B
考点:分式方程的实际应用
解:首先设甲车间每天能生产x个,则乙车间每天能生产1.5x个,由题意可得等量关系:甲车间生产2700件所用的时间+甲乙两车间生产2700件所用的时间=30天,根据等量关系可列出方程 2700x+2700x+1.5x=30 .
故答案为:B.
分析:先设甲车间每天能生产x个,则乙车间每天能生产1.5x个,根据“甲车间生产2700件所用的时间+甲乙两车间生产2700件所用的时间=30天”列出方程即可.
7. B
考点:分式方程的实际应用
解:设这个容器的容积为x升,
由题意得:x﹣10﹣6× x-10x = 77+13 x,
整理得:13x2﹣320x+1200=0,
解得:x=20,或x= 6013 (舍去),
∴x=20,
经检验,x=20是原分式方程的解;
即这个容器的容积为20升;
故答案为:B.
分析:设这个容器的容积为x升,由容器中剩余酒精的量的不同表示方法列出分式方程,然后解分式方程,再检验即可.
8. D
考点:分式方程的实际应用
解:设原计划每天铺设管道 x 米,则实际每天铺设管道 (1+10%)x ,
根据题意,可列方程: 660x-660x(1+10%)=6 ,
所以小明所列方程中未知数 x 所表示的量是计划每天铺设管道的长度,
故答案为:D.
分析:根据计划所用时间-实际所用时间=6,可知方程中未知数x所表示的量.
9. A
考点:分式方程的实际应用
解:设乙厂房每天生产x箱口罩,则甲厂房每天生产2x箱口罩,
依题意得: 6000x-60002x=5 ,
解得:x=600,
经检验,x=600是原分式方程的解,且符合题意,
∴2x=1200.
故答案选:A .
分析:先设乙厂房每天生产x箱口罩,则甲厂房每天生产2x箱口罩,根据工作时间=工作总量÷工作效率且两厂房各加工6000箱口罩时甲厂房比乙厂房少用5天,可得出关于x的分式方程,解方程即可得出结论.
10. B
考点:分式方程的实际应用
解:设工作总量为1,规定日期为x天,则若单独做,甲队需(x+1)天,乙队需(x+4)天,根据题意列方程得
3( 1x+1+1x+4 )+ x-3x+4 =1,
解方程可得x=8,
经检验x=8是分式方程的解,
故答案为:B.
分析:先设规定日期为x,再用x表示出甲、乙的工作效率,最后利用工作总量列出方程即可。
二、填空题
11. 600
考点:分式方程的实际应用
解:设乙骑自行车的速度为x米/分钟,则甲步行速度是 12 x米/分钟,公交车的速度是2x米/分钟,
根据题意得
60012x+3000-6002x=3000x-2 ?,
解得:x=300米/分钟,
经检验x=300是方程的根,
则乙骑自行车的速度为300米/分钟.
那么甲同学到达学校时,乙同学离学校还=2×300=600米.
故答案为:600.
分析:设乙骑自行车的速度为x米/分钟,则甲步行速度是 12 x米/分钟,公交车的速度是2x米/分钟,根据题意找到等量关系:甲步行的时间+甲公车时间=乙的时间-2分钟,列方程即可得到乙的速度,甲同学到达学校时,乙同学离学校还有2x米,即可得到结论;
12. 1214x-1215x=13
考点:分式方程的实际应用
解:设甲车平均速度为4x千米/小时,则乙车平均速度为5x千米/小时,根据题意得:
1214x-1215x=13.
故答案为: 1214x-1215x=13.
分析:设甲车平均速度为4x千米/小时,则乙车平均速度为5x千米/小时,根据“ 两车同时从A地出发到B地,乙车比甲车早到20分钟 ”列出方程即可.
13. 2700x=4500x+20
考点:列分式方程
解:设A型陶笛的单价为x元,则B型陶笛的单价为(x+20)元,根据用2700元购买A型陶笛与用4500元购买B型陶笛的数量相同,可得 2700x=4500x+20 .
故答案为: 2700x=4500x+20 .
分析:设A型陶笛的单价为x元,则B型陶笛的单价为(x+20)元,根据“根据用2700元购买A型陶笛与用4500元购买B型陶笛的数量相同”列出方程即可。
14. (1)800x+10=600x;800y=600y+10
(2)30
考点:解分式方程,列分式方程
解:(1)设乙型机器人每小时搬运 xkg 产品,则甲型机器人每小时搬运(x+10)kg,由题意得
800x+10=600x ,
设甲型机器人搬运 800kg 所用时间为 y 小时,由题意得
800y=600y+10 ,
故答案为: 800x+10=600x , 800y=600y+10 ;
(2)设乙型机器人每小时搬运 xkg 产品,则甲型机器人每小时搬运(x+10)kg,由题意得
800x+10=600x ,
解得x=30,
经检验,x=30是方程的解,
答:乙型机器人每小时搬运产品30kg.
故答案为:30.
分析:(1)设乙型机器人每小时搬运 xkg 产品,根据甲型机器人搬运 800kg 所用时间与乙型机器人搬运 600kg 所用时间相等列方程;设甲型机器人搬运 800kg 所用时间为 y 小时,根据甲型机器人比乙型机器人每小时多搬运 10kg 列方程;(2)设乙型机器人每小时搬运 xkg 产品,则甲型机器人每小时搬运(x+10)kg,由题意得 800x+10=600x ,解方程即可.
三、解答题
15. 解:设原来长方形的长是x厘米,则新长方形的长是 2x 厘米.
390x-3902x=13
解得 x=15
经检验, x=15 是原方程的解,且符合题意.
答:原长方形的长是15厘米.
考点:分式方程的实际应用
分析:设原来长方形的长是x厘米,则新长方形的长是 2x 厘米,根据原长方形的宽-新长方形的宽=13m,列出方程,解之并检验即可.
16. 解:设第一次购买水果的进价是每千克 x 元,
依题意得: 1200x=1430x(1+20%)-20 ,
解之得: x=5 ,
经检验, x=5 是原方程的解并符合题意,
所以,原方程的解是 x=5 .
答:第一次购买水果的进价是每千克5元.
考点:分式方程的实际应用
分析:设第一次购买水果的进价是每千克 x 元,根据第二次购买的水果的数量比第一次多20千克列方程求解即可.
17. (1)1.5x;120x;1201.5x
(2)解:设大巴的平均速度为x公里/小时,则小车的平均速度为1.5x公里/小时,
根据题意,得: 120x=12+1201.5x+16
解得:x=60,
经检验:x=60是原方程的解,
答:大巴的平均速度为60公里/小时,则小车的平均速度为90公里/小时;
(3)解:设苏老师赶上大巴的地点到基地的路程有y公里,
根据题意,得: 120-y60=120-y90+12
解得:y=30,
答:苏老师追上大巴车的地点到基地的路程有30公里.
考点:解分式方程,分式方程的实际应用
解:(1)
?
速度(km/h)
路程(km)
时间(h)
大巴车
x
120
120x
小汽车
1.5x
120
1201.5x
分析:(1)根据小汽车的速度=大巴车的速度×1.5,用含x的代数式表示出小汽车的速度;再利用时间=路程÷速度,分别用含x的代数式表示出两车的时间。
(2)抓住关键语句: 队伍乘大巴车8:00从学校出发;苏老师8:30从学校自驾小汽车出发,结果比队伍提前10分钟到达基地.; 此题的等量关系为:大巴车行驶120千米的路程所用的时间=小汽车行驶120千米的时间+12+16 , 设未知数列方程,再解方程检验,即可求解。
(3)抓住已知条件:苏老师自驾小汽车追上大巴车后继续前行,结果比队伍提前10分钟到达基地.,据此设未知数,列方程求解即可。
18. (1)解:由图可得:甲块木板的面积:(ab+10a)平方厘米;乙块木板的面积:(10a+10b)平方厘米;丙块木板的面积:(ab+10b)平方厘米;
(2)解:由题意可得: {ab+10a-(ab+10b)=20010ab=150000 ,
即 {a-b=20ab=15000 ,
则(a+b)2=(a﹣b)2+4ab=400+60000=60400,
则乙块木板的面积为10a+10b=10(a+b)=10 60400 =200 151 (cm2);
(3)解:由题意可得: ab+10a+10a+10b+ab+10b100(a+b) =90%,
化简得ab=35(a+b),
则 5a + 5b + a2b-ab27a2-7b2
= 5(a+b)ab + ab(a-b)7(a+b)(a-b)
= 5(a+b)ab + ab7(a+b)
= 5(a+b)35(a+b) + 35(a+b)7(a+b)
= 17 +5
= 367 .
考点:分式方程的实际应用,二元一次方程组的应用-几何问题
分析:(1)利用展开图,结合立体图形的边长即可得出答案;
(2)利用“甲块木板的面积比丙块木板的面积大200平方厘米,木箱的体积为150000立方厘米”,结合(1)中所求得出等式即可求解;
(3)利用(1)中所求表示出箱子的侧面积以及木板的利用率为90%,得出等式求出ab=35(a+b),再代入计算即可求解.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
