6.5频数直方图 同步练习(含解析)
图片预览



文档简介
初中数学浙教版七年级下册6.5频数直方图 同步练习
一、单选题
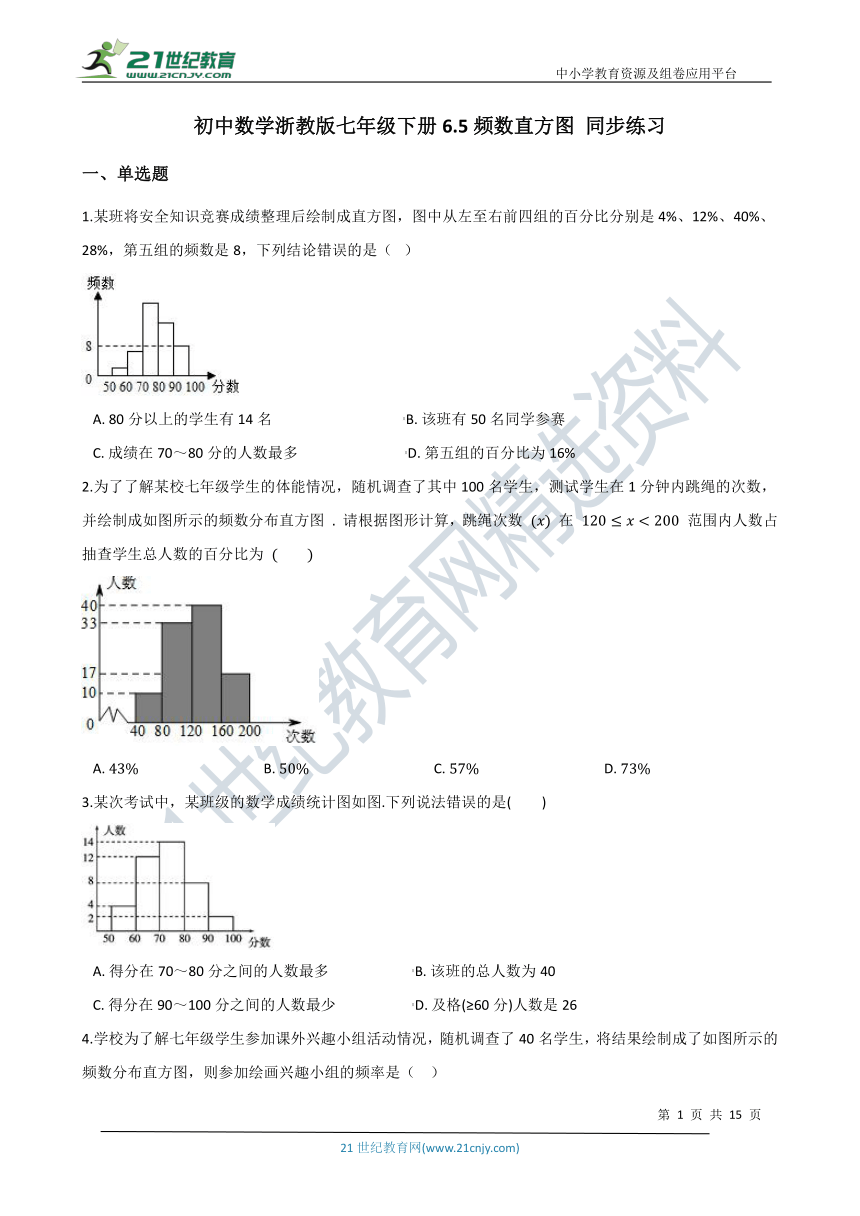
1.某班将安全知识竞赛成绩整理后绘制成直方图,图中从左至右前四组的百分比分别是4%、12%、40%、28%,第五组的频数是8,下列结论错误的是( ?)
A.?80分以上的学生有14名??????????????????????????????????????B.?该班有50名同学参赛
C.?成绩在70~80分的人数最多???????????????????????????????D.?第五组的百分比为16%
2.为了了解某校七年级学生的体能情况,随机调查了其中100名学生,测试学生在1分钟内跳绳的次数,并绘制成如图所示的频数分布直方图 . 请根据图形计算,跳绳次数 (x) 在 120≤x<200 范围内人数占抽查学生总人数的百分比为 ( ?? )
A.?43%????????????????????????????????????B.?50%????????????????????????????????????C.?57%????????????????????????????????????D.?73%
3.某次考试中,某班级的数学成绩统计图如图.下列说法错误的是( )
A.?得分在70~80分之间的人数最多????????????????????????B.?该班的总人数为40
C.?得分在90~100分之间的人数最少??????????????????????D.?及格(≥60分)人数是26
4.学校为了解七年级学生参加课外兴趣小组活动情况,随机调查了40名学生,将结果绘制成了如图所示的频数分布直方图,则参加绘画兴趣小组的频率是(?? )
A.?0.1???????????????????????????????????????B.?0.15?????????????????????????????????????C.?0.25???????????????????????????????????????D.?0.3
5.小聪对他所在小区居民每天微信阅读时间进行了抽样调查,并绘制成了如图所示的统计图.根据图中信息,其中正确的是( )
①小聪一共抽样调查了60人
②每天微信阅读时间多于50分钟的人数有12人
③每天微信阅读时间30~40分钟的人数最多
④每天微信阅读时间不足30分钟的人数多于调查总人数的一半
A.?①②?????????????????????????????????????B.?②③?????????????????????????????????????C.?②④?????????????????????????????????????D.?③④
6.为了了解本校八年级学生的体能情况,随机抽查了其中30名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的频数分布直方图,则仰卧起坐次数在25次(含25次)以上的人数共有(???? )
A.?10人???????????????????????????????????B.?12人???????????????????????????????????C.?17人???????????????????????????????????D.?都不对
7.如图是某班级的一次数学考试成绩(得分均为整数)的频数分布直方图(每组包含最小值,不包含最大值),则下列说法不正确的是( )
A.?得分在70~79分的人数最多???????????????????????????????B.?人数最少的得分段的频数为2
C.?得分及格(≥60分)的有12人?????????????????????????????D.?该班的总人数为40人
8.某校测量了初三 (1) 班学生的身高(精确到 1cm ),按 10cm 为一段进行分组,得到如下频数分布直方图,则下列说法正确的是(? ?)
A.?该班人数最多的身高段的学生数为 人?????????????B.?该班身高低于 的学生数为 人
C.?该班身高最高段的学生数为 人??????????????????????D.?该班身高最高段的学生数为 人
9.下列有关频数分布表和频数分布直方图的理解,正确的是(??? )
A.?频数分布表能清楚地反映事物的变化情况???????????
B.?频数分布直方图能清楚地反映事物的变化情况
C.?频数分布直方图能清楚地表示出各部分在总体中所占的百分比?????????
D.?二者均不能清楚地反映变化情况和在总体中所占的百分比,但能反映出每个项目的具体数目
10.如图是某班45名同学爱心捐款额的频数分布直方图(每组含前一个边界值,不含后一个边界值),则捐款人数最多的一组是(??? )
A.?5~10元?????????????????????????????B.?10~15?????????????????????????????C.?15~20元?????????????????????????????D.?20~25元
二、填空题
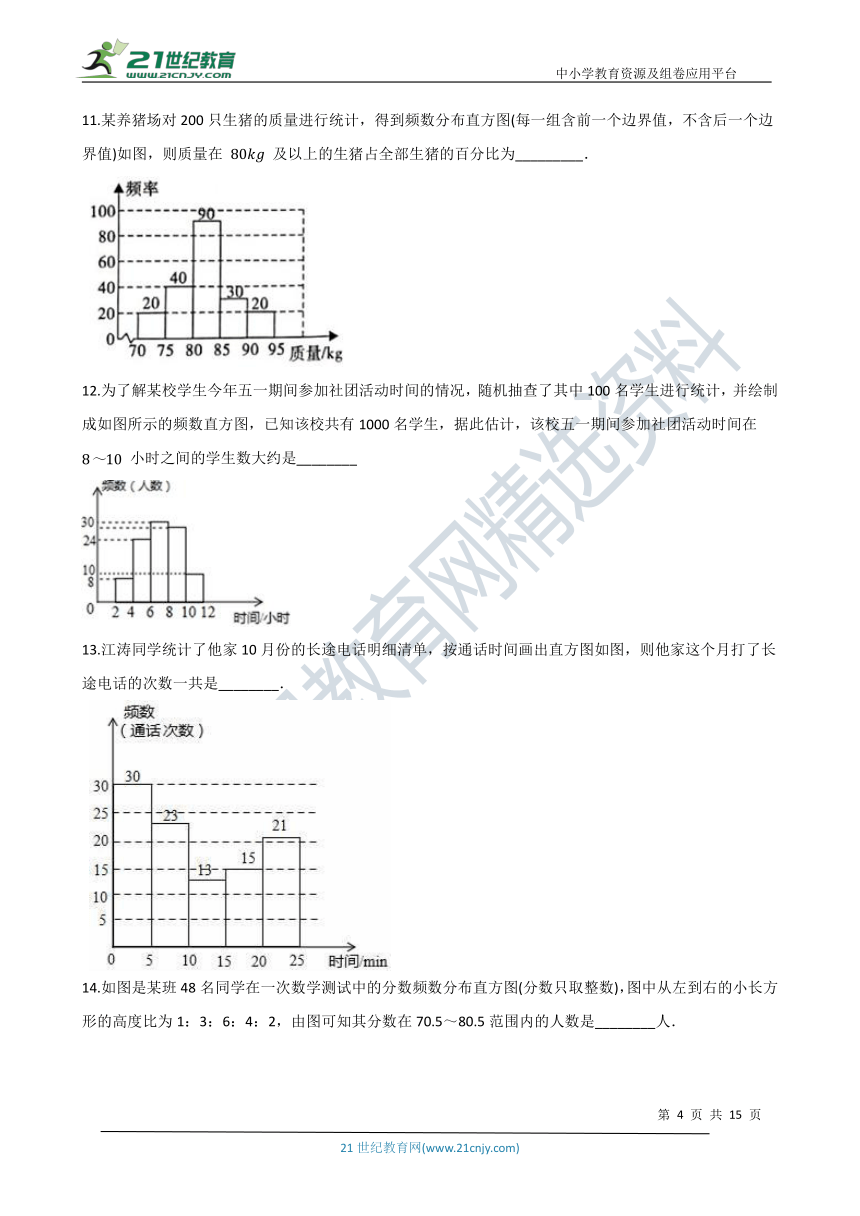
11.某养猪场对200只生猪的质量进行统计,得到频数分布直方图(每一组含前一个边界值,不含后一个边界值)如图,则质量在 80kg 及以上的生猪占全部生猪的百分比为_________.
12.为了解某校学生今年五一期间参加社团活动时间的情况,随机抽查了其中100名学生进行统计,并绘制成如图所示的频数直方图,已知该校共有1000名学生,据此估计,该校五一期间参加社团活动时间在 8~10 小时之间的学生数大约是________
13.江涛同学统计了他家10月份的长途电话明细清单,按通话时间画出直方图如图,则他家这个月打了长途电话的次数一共是________.
14.如图是某班48名同学在一次数学测试中的分数频数分布直方图(分数只取整数),图中从左到右的小长方形的高度比为1:3:6:4:2,由图可知其分数在70.5~80.5范围内的人数是________人.
15.某班学生参加环保知识竞赛,已知竞赛得分都是整数,把参赛学生的成绩整理后分为6小组,画出竞赛成绩的频数分布直方图(如图所示),根据图中的信息可得,成绩不及格(低于60分)的学生占全班参赛人数的百分率是 ________
三、综合题
16.为了解居民月用水量,某市对某区居民用水量进行了抽样调查,并制成如下直方图.
(1)这次一共抽查了________户;
(2)用水量不足10吨的有________户,用水量超过16吨的有________户;
(3)假设该区有8万户居民,估计用水量少于10吨的有多少户?
17.课外兴趣小组为了解某段路上机动车的车速,抽查了一段时间内若干辆车的车速(车速取整数,单位:千米/时)并制成如图所示的频数分布直方图.已知车速在41千米/时到50千米/时的车辆数占车辆总数的 29 .
(1)在这段时间内他们抽查的车有________辆;
(2)被抽查车辆的车速的中位数所在速度段(单位:千米/时)是(?? )
A.30.5~40.5
B.40.5~50.5
C.50.5~60.5
D.60.5~70.5
(3)补全频数分布直方图;
(4)如果全天超速(车速大于60千米/时)的车有200辆,则当天的车流量约为多少辆?
18.某学校为了解八年级学生的身体素质情况,随机抽取了八年级 40 名学生进行一分钟跳绳个数测试,以测试数据为样本,绘制出频数分布表和频数分布直方图,如下所示:
八年级 40 名学生跳绳个数频数分布表
组别
分组/个
频数
第 1 组
80≤x<100
4
第 2 组
100≤x<120
8
第 3 组
120≤x<140
m
第 4 组
140≤x<160
12
第 5 组
160≤x<180
3
八年级 40 名学生跳绳个数频数分布直方图
请结合图表完成下列问题:
(1)表中的 m =________;
(2)请把频数分布直方图补充完整;
(3)已知八年级学生一分钟跳绳个数的成绩标准是:x<120 为不合格;120≤x<140 为合格;140≤x<160 为良;x≥160 为优.如果该年级有 360 名学生,根据以上信息,请你估算该年级跳绳不合格的人数约为________名,成绩为优的人数约为________名.
答案解析部分
一、单选题
1. A
考点:频数(率)分布直方图
解:本班参赛的学生有:8÷(1﹣4%﹣12%﹣40%﹣28%)=50(人),故B选项正确;
80分以上的学生有:50×28%+8=22(名),故A选项错误;
成绩在70~80分的人数最多,故C选项正确;
第五组的百分比为:8÷50×100%=16%,故D选项正确.
故答案为:A.
分析:根据题意和频数分布直方图中的数据,可以计算出本班参赛的学生,然后即可判断各个选项中的说法是否正确,从而可以解答本题.
2. C
考点:频数(率)分布直方图
解:总人数为10+33+40+17=100人,
120≤x<200范围内人数为40+17=57人,
在120≤x<200范围内人数占抽查学生总人数的百分比为 57100 =57%.
故答案为:C.
分析:?利用频数分布直方图求出总人数及120≤x<200范围内人数,由120≤x<200范围内人数抽查的总人数×100%计算即可.
3. D
考点:频数(率)分布直方图
解:A、得分在70~80分之间的人数最多,故正确,不符合题意;
B、2+4+8+12+14=40(人),该班的总人数为40人,故正确,不符合题意;
C、得分在90~100分之间的人数最少,有2人,故正确,不符合题意;
D、40-4=36(人),及格(≥60分)人数是36人,故错误,符合题意.
故答案为:D.
分析:为了判断得分在70~80分之间的人数是不是最多,通过观察频率分布直方图中最高的小矩形即可;为了得到该班的总人数只要求出各组人数的和即可;为了看得分在90~100分之间的人数是否最少,只有观察频率分布直方图中最低的小矩形即可;为了得到及格(≥60分)人数可通过用总数减去第一小组的人数即可.
4. D
考点:频数(率)分布直方图
解:∵根据频率分布直方图知道绘画兴趣小组的频数为12,∴参加绘画兴趣小组的频率是12÷40=0.3.
分析:利用绘画兴趣小组的频数除以随机调查的总人数即可.
5. B
考点:频数(率)分布直方图
解:①小聪一共抽样调查了4+8+14+20+16+12=74人,故①不符合题意;
②每天微信阅读时间多于50分钟的人数有12人,故②符合题意;
③每天微信阅读时间30~40分钟的人数为20人,最多,故③符合题意;
④每天微信阅读时间不足30分钟的人数有4+8+14=26人,占调查总人数的百分比为 2674×100%<3774×100%=50% ,故④不符合题意.
故正确的有②③;
故答案为:B.
分析:根据直方图表示的意义求得统计的总人数,以及每组(类)的人数即可判断
6. C
考点:频数(率)分布直方图
解:从频数分布直方图可知,1分钟仰卧起坐的次数在25~30次的有12人,在30~35次的有5人,
因此仰卧起坐次数在25次(含25次)以上的人数共有12+5=17(人),
故答案为:C.
分析:从频数分布直方图中可以得出答案.
7. C
考点:频数(率)分布直方图
解:A、得分在70~79分的人数最多,符合题意,本选项不符合题意.
B、人数最少的得分段的频数为2,符合题意,本选项不符合题意.
C、得分及格(≥60分)的有12人,不符合题意,本选项符合题意.
D、该班的总人数为40人,符合题意,本选项不符合题意.
故答案为:C.
分析:根据频数分别直方图可得得分在70~79分的人数14人最多,人数最少的90~100的认识最少2人,及格(≥60分)的有12+14+8+2=36人;该班总人数为4+12+14+8+2=40人,据此逐一判断即可.
8. D
考点:频数(率)分布直方图
解:A、该班人数最多的身高段的学生数为20人,故A不符合题意;
B、该班身高低于 160.5cm 的学生数为20人,故B不符合题意;
C、该班身高最高段的学生数为7人,故C不符合题意;
D、该班身高最高段的学生数为7人,故D符合题意;
故答案为:D
分析:由频数分布直方图可以得到相关信息:该班人数最多的身高段的学生数为20人;该班身高低于 160.5cm 的学生数为20人;该班身高最高段的学生数为7人,即可得出答案。
9. D
考点:频数(率)分布直方图
解:A、频数分布表能清楚的反映落在每个小组内的数据情况,不能清楚的反映事物的变化情况,故此选项不符合题意;
B、频数分布图能清楚的反映落在每个小组内的数据多少,折线图能反映事物的变化情况,故此选项不符合题意;
C、扇形图能清楚地表示出各部分在总体中所占的百分比,直方图不能,故此选项不符合题意;
D、二者均不能清楚地反映变化情况和在总体中所占的百分比,但能反映出每个项目的具体数目,故此选项不符合题意.
故答案为:D.
分析:频数分布表能清楚的反映落在每个小组内的数据情况,可对A作出判断;频数分布图能清楚的反映落在每个小组内的数据多少,折线图能反映事物的变化情况,可对B作出判断;扇形图能清楚地表示出各部分在总体中所占的百分比,直方图不能,可对C作出判断;二者均不能清楚地反映变化情况和在总体中所占的百分比,但能反映出每个项目的具体数目,可对D作出判断,即可得出答案。
10. C
考点:频数(率)分布直方图
解:根据图形所给出的数据可得:
15-20元的有20人,人数最多,
则捐款人数最多的一组是15-20元;
故答案为:C.
分析:根据图形所给出的数据可得15-20元的有20人,人数最多,得到捐款人数最多的一组是15-20元.
二、填空题
11. 70%
考点:频数(率)分布直方图
解:质量在80kg以上的生猪所占的百分比为90+30+20200×100%=70%.
故答案为:70%.
分析:利用质量在80kg以上的生猪的数量除以200,列式计算可求解。
12. 280
考点:频数(率)分布直方图
解:由题意可得,
条形统计图中,8~10有学生:100?8?24?30?10=28(名),
则该校五一期间参加社团活动时间在8~10小时之间的学生数大约是:1000× 28100 =280,
故答案为:280.
分析:根据条形统计图中的数据可以计算出统计图中8~10小时之间的学生数,从而可以估计该校五一期间参加社团活动时间在8~10小时之间的学生数.
13. 102次
考点:频数(率)分布直方图
解:这个月打了长途电话的次数=30+23+13+15+21=102(次),
故答案为102次.
分析:根据直方图中的信息,将每个时间段内的次数相加即得总次数.
14. 18
考点:频数(率)分布直方图
解:分数在70.5~80.5范围内的人数=48× 61+3+6+4+2 =18.
故答案为:18.
分析:利用小长方形的高度比为1:3:6:4:2得到分数在70.5~80.5范围内的人数的频率,然后用48乘以此组的频率得到该组的频数.
15. 20%
考点:频数(率)分布直方图
解:全班参赛人数为,3+6+7+6+11+12=45(人)
∴成绩不及格的百分率为945×100%=20%
分析:根据题意,计算得到参与调查的总人数,根据不及格的人数计算得到百分率即可。
三、综合题
16. (1)100
(2)55;10
(3)55100×80000=44000 (户)
∴估计该区居民用水量少于10吨的有44 000户.
考点:频数(率)分布直方图
解: :(1)20+35+20+15+5+5=100 (户)
∴这次一共抽查了100户;
(2)①20+35=55 (户),②5+5=10 (户)
∴用水量不足10吨的有55户,用水量超过16吨的有10户;
(3)55100×80000=44000 (户)
∴估计该区居民用水量少于10吨的有44 000户.
分析:(1)根据直方图,把用水量在各个段的户数加起来即可得到一共抽查的户数;
(2)根据直方图,把用水量不足10吨的户数加起来即可,把,用水量超过16吨的户数加起来即可;
(3)用该区居民用水量少于10吨的户数所占的百分比×80000,就可得出答案。
17. (1)45
(2)C
(3)解:补全的频数分布直方图如下图所示,
(4)解:200÷ 845 =1125(辆)?
答:当天的车流量约为1125辆.
考点:频数(率)分布直方图
解:(1)观察统计图知:车速在41千米/时到50千米/时的车辆数为10,占总数的 29 ,
所以,10÷ 29 =45;
故答案为:45;
( 2? )∵共45辆车,
∴中位数为第23辆车的速度,
∴50.5~60.5
故答案为:C.
分析:(1)用车速在41千米/时到50千米/时的车辆数除以 29 即可得到;
(2)根据车辆总数确定第23辆车为中位数,根据每一小组的频数确定中位数所处的小组即可;
(3)用总数减去其他小组的频数即可得到50.5~60.5小组的频数即可补全统计图;
(4)用200除以车速车速大于60千米/时的车辆所占的百分比即可求得车流量.
18. (1)13
(2)解:如图:
(3)108;27
考点:频数(率)分布直方图
解:(1)表中的m=40-4-8-12-3=13;(3)该年级跳绳不合格的人数约为360× 4+840=108 ,
成绩为优的人数约是360× 340=27 .
故答案是:108,27.
分析:(1)利用总数40减去其它组的频数即可求得;(2)根据(1)即可直接补全直方图;(3)利用总数360乘以对应的比例即可求解.
一、单选题
1.某班将安全知识竞赛成绩整理后绘制成直方图,图中从左至右前四组的百分比分别是4%、12%、40%、28%,第五组的频数是8,下列结论错误的是( ?)
A.?80分以上的学生有14名??????????????????????????????????????B.?该班有50名同学参赛
C.?成绩在70~80分的人数最多???????????????????????????????D.?第五组的百分比为16%
2.为了了解某校七年级学生的体能情况,随机调查了其中100名学生,测试学生在1分钟内跳绳的次数,并绘制成如图所示的频数分布直方图 . 请根据图形计算,跳绳次数 (x) 在 120≤x<200 范围内人数占抽查学生总人数的百分比为 ( ?? )
A.?43%????????????????????????????????????B.?50%????????????????????????????????????C.?57%????????????????????????????????????D.?73%
3.某次考试中,某班级的数学成绩统计图如图.下列说法错误的是( )
A.?得分在70~80分之间的人数最多????????????????????????B.?该班的总人数为40
C.?得分在90~100分之间的人数最少??????????????????????D.?及格(≥60分)人数是26
4.学校为了解七年级学生参加课外兴趣小组活动情况,随机调查了40名学生,将结果绘制成了如图所示的频数分布直方图,则参加绘画兴趣小组的频率是(?? )
A.?0.1???????????????????????????????????????B.?0.15?????????????????????????????????????C.?0.25???????????????????????????????????????D.?0.3
5.小聪对他所在小区居民每天微信阅读时间进行了抽样调查,并绘制成了如图所示的统计图.根据图中信息,其中正确的是( )
①小聪一共抽样调查了60人
②每天微信阅读时间多于50分钟的人数有12人
③每天微信阅读时间30~40分钟的人数最多
④每天微信阅读时间不足30分钟的人数多于调查总人数的一半
A.?①②?????????????????????????????????????B.?②③?????????????????????????????????????C.?②④?????????????????????????????????????D.?③④
6.为了了解本校八年级学生的体能情况,随机抽查了其中30名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的频数分布直方图,则仰卧起坐次数在25次(含25次)以上的人数共有(???? )
A.?10人???????????????????????????????????B.?12人???????????????????????????????????C.?17人???????????????????????????????????D.?都不对
7.如图是某班级的一次数学考试成绩(得分均为整数)的频数分布直方图(每组包含最小值,不包含最大值),则下列说法不正确的是( )
A.?得分在70~79分的人数最多???????????????????????????????B.?人数最少的得分段的频数为2
C.?得分及格(≥60分)的有12人?????????????????????????????D.?该班的总人数为40人
8.某校测量了初三 (1) 班学生的身高(精确到 1cm ),按 10cm 为一段进行分组,得到如下频数分布直方图,则下列说法正确的是(? ?)
A.?该班人数最多的身高段的学生数为 人?????????????B.?该班身高低于 的学生数为 人
C.?该班身高最高段的学生数为 人??????????????????????D.?该班身高最高段的学生数为 人
9.下列有关频数分布表和频数分布直方图的理解,正确的是(??? )
A.?频数分布表能清楚地反映事物的变化情况???????????
B.?频数分布直方图能清楚地反映事物的变化情况
C.?频数分布直方图能清楚地表示出各部分在总体中所占的百分比?????????
D.?二者均不能清楚地反映变化情况和在总体中所占的百分比,但能反映出每个项目的具体数目
10.如图是某班45名同学爱心捐款额的频数分布直方图(每组含前一个边界值,不含后一个边界值),则捐款人数最多的一组是(??? )
A.?5~10元?????????????????????????????B.?10~15?????????????????????????????C.?15~20元?????????????????????????????D.?20~25元
二、填空题
11.某养猪场对200只生猪的质量进行统计,得到频数分布直方图(每一组含前一个边界值,不含后一个边界值)如图,则质量在 80kg 及以上的生猪占全部生猪的百分比为_________.
12.为了解某校学生今年五一期间参加社团活动时间的情况,随机抽查了其中100名学生进行统计,并绘制成如图所示的频数直方图,已知该校共有1000名学生,据此估计,该校五一期间参加社团活动时间在 8~10 小时之间的学生数大约是________
13.江涛同学统计了他家10月份的长途电话明细清单,按通话时间画出直方图如图,则他家这个月打了长途电话的次数一共是________.
14.如图是某班48名同学在一次数学测试中的分数频数分布直方图(分数只取整数),图中从左到右的小长方形的高度比为1:3:6:4:2,由图可知其分数在70.5~80.5范围内的人数是________人.
15.某班学生参加环保知识竞赛,已知竞赛得分都是整数,把参赛学生的成绩整理后分为6小组,画出竞赛成绩的频数分布直方图(如图所示),根据图中的信息可得,成绩不及格(低于60分)的学生占全班参赛人数的百分率是 ________
三、综合题
16.为了解居民月用水量,某市对某区居民用水量进行了抽样调查,并制成如下直方图.
(1)这次一共抽查了________户;
(2)用水量不足10吨的有________户,用水量超过16吨的有________户;
(3)假设该区有8万户居民,估计用水量少于10吨的有多少户?
17.课外兴趣小组为了解某段路上机动车的车速,抽查了一段时间内若干辆车的车速(车速取整数,单位:千米/时)并制成如图所示的频数分布直方图.已知车速在41千米/时到50千米/时的车辆数占车辆总数的 29 .
(1)在这段时间内他们抽查的车有________辆;
(2)被抽查车辆的车速的中位数所在速度段(单位:千米/时)是(?? )
A.30.5~40.5
B.40.5~50.5
C.50.5~60.5
D.60.5~70.5
(3)补全频数分布直方图;
(4)如果全天超速(车速大于60千米/时)的车有200辆,则当天的车流量约为多少辆?
18.某学校为了解八年级学生的身体素质情况,随机抽取了八年级 40 名学生进行一分钟跳绳个数测试,以测试数据为样本,绘制出频数分布表和频数分布直方图,如下所示:
八年级 40 名学生跳绳个数频数分布表
组别
分组/个
频数
第 1 组
80≤x<100
4
第 2 组
100≤x<120
8
第 3 组
120≤x<140
m
第 4 组
140≤x<160
12
第 5 组
160≤x<180
3
八年级 40 名学生跳绳个数频数分布直方图
请结合图表完成下列问题:
(1)表中的 m =________;
(2)请把频数分布直方图补充完整;
(3)已知八年级学生一分钟跳绳个数的成绩标准是:x<120 为不合格;120≤x<140 为合格;140≤x<160 为良;x≥160 为优.如果该年级有 360 名学生,根据以上信息,请你估算该年级跳绳不合格的人数约为________名,成绩为优的人数约为________名.
答案解析部分
一、单选题
1. A
考点:频数(率)分布直方图
解:本班参赛的学生有:8÷(1﹣4%﹣12%﹣40%﹣28%)=50(人),故B选项正确;
80分以上的学生有:50×28%+8=22(名),故A选项错误;
成绩在70~80分的人数最多,故C选项正确;
第五组的百分比为:8÷50×100%=16%,故D选项正确.
故答案为:A.
分析:根据题意和频数分布直方图中的数据,可以计算出本班参赛的学生,然后即可判断各个选项中的说法是否正确,从而可以解答本题.
2. C
考点:频数(率)分布直方图
解:总人数为10+33+40+17=100人,
120≤x<200范围内人数为40+17=57人,
在120≤x<200范围内人数占抽查学生总人数的百分比为 57100 =57%.
故答案为:C.
分析:?利用频数分布直方图求出总人数及120≤x<200范围内人数,由120≤x<200范围内人数抽查的总人数×100%计算即可.
3. D
考点:频数(率)分布直方图
解:A、得分在70~80分之间的人数最多,故正确,不符合题意;
B、2+4+8+12+14=40(人),该班的总人数为40人,故正确,不符合题意;
C、得分在90~100分之间的人数最少,有2人,故正确,不符合题意;
D、40-4=36(人),及格(≥60分)人数是36人,故错误,符合题意.
故答案为:D.
分析:为了判断得分在70~80分之间的人数是不是最多,通过观察频率分布直方图中最高的小矩形即可;为了得到该班的总人数只要求出各组人数的和即可;为了看得分在90~100分之间的人数是否最少,只有观察频率分布直方图中最低的小矩形即可;为了得到及格(≥60分)人数可通过用总数减去第一小组的人数即可.
4. D
考点:频数(率)分布直方图
解:∵根据频率分布直方图知道绘画兴趣小组的频数为12,∴参加绘画兴趣小组的频率是12÷40=0.3.
分析:利用绘画兴趣小组的频数除以随机调查的总人数即可.
5. B
考点:频数(率)分布直方图
解:①小聪一共抽样调查了4+8+14+20+16+12=74人,故①不符合题意;
②每天微信阅读时间多于50分钟的人数有12人,故②符合题意;
③每天微信阅读时间30~40分钟的人数为20人,最多,故③符合题意;
④每天微信阅读时间不足30分钟的人数有4+8+14=26人,占调查总人数的百分比为 2674×100%<3774×100%=50% ,故④不符合题意.
故正确的有②③;
故答案为:B.
分析:根据直方图表示的意义求得统计的总人数,以及每组(类)的人数即可判断
6. C
考点:频数(率)分布直方图
解:从频数分布直方图可知,1分钟仰卧起坐的次数在25~30次的有12人,在30~35次的有5人,
因此仰卧起坐次数在25次(含25次)以上的人数共有12+5=17(人),
故答案为:C.
分析:从频数分布直方图中可以得出答案.
7. C
考点:频数(率)分布直方图
解:A、得分在70~79分的人数最多,符合题意,本选项不符合题意.
B、人数最少的得分段的频数为2,符合题意,本选项不符合题意.
C、得分及格(≥60分)的有12人,不符合题意,本选项符合题意.
D、该班的总人数为40人,符合题意,本选项不符合题意.
故答案为:C.
分析:根据频数分别直方图可得得分在70~79分的人数14人最多,人数最少的90~100的认识最少2人,及格(≥60分)的有12+14+8+2=36人;该班总人数为4+12+14+8+2=40人,据此逐一判断即可.
8. D
考点:频数(率)分布直方图
解:A、该班人数最多的身高段的学生数为20人,故A不符合题意;
B、该班身高低于 160.5cm 的学生数为20人,故B不符合题意;
C、该班身高最高段的学生数为7人,故C不符合题意;
D、该班身高最高段的学生数为7人,故D符合题意;
故答案为:D
分析:由频数分布直方图可以得到相关信息:该班人数最多的身高段的学生数为20人;该班身高低于 160.5cm 的学生数为20人;该班身高最高段的学生数为7人,即可得出答案。
9. D
考点:频数(率)分布直方图
解:A、频数分布表能清楚的反映落在每个小组内的数据情况,不能清楚的反映事物的变化情况,故此选项不符合题意;
B、频数分布图能清楚的反映落在每个小组内的数据多少,折线图能反映事物的变化情况,故此选项不符合题意;
C、扇形图能清楚地表示出各部分在总体中所占的百分比,直方图不能,故此选项不符合题意;
D、二者均不能清楚地反映变化情况和在总体中所占的百分比,但能反映出每个项目的具体数目,故此选项不符合题意.
故答案为:D.
分析:频数分布表能清楚的反映落在每个小组内的数据情况,可对A作出判断;频数分布图能清楚的反映落在每个小组内的数据多少,折线图能反映事物的变化情况,可对B作出判断;扇形图能清楚地表示出各部分在总体中所占的百分比,直方图不能,可对C作出判断;二者均不能清楚地反映变化情况和在总体中所占的百分比,但能反映出每个项目的具体数目,可对D作出判断,即可得出答案。
10. C
考点:频数(率)分布直方图
解:根据图形所给出的数据可得:
15-20元的有20人,人数最多,
则捐款人数最多的一组是15-20元;
故答案为:C.
分析:根据图形所给出的数据可得15-20元的有20人,人数最多,得到捐款人数最多的一组是15-20元.
二、填空题
11. 70%
考点:频数(率)分布直方图
解:质量在80kg以上的生猪所占的百分比为90+30+20200×100%=70%.
故答案为:70%.
分析:利用质量在80kg以上的生猪的数量除以200,列式计算可求解。
12. 280
考点:频数(率)分布直方图
解:由题意可得,
条形统计图中,8~10有学生:100?8?24?30?10=28(名),
则该校五一期间参加社团活动时间在8~10小时之间的学生数大约是:1000× 28100 =280,
故答案为:280.
分析:根据条形统计图中的数据可以计算出统计图中8~10小时之间的学生数,从而可以估计该校五一期间参加社团活动时间在8~10小时之间的学生数.
13. 102次
考点:频数(率)分布直方图
解:这个月打了长途电话的次数=30+23+13+15+21=102(次),
故答案为102次.
分析:根据直方图中的信息,将每个时间段内的次数相加即得总次数.
14. 18
考点:频数(率)分布直方图
解:分数在70.5~80.5范围内的人数=48× 61+3+6+4+2 =18.
故答案为:18.
分析:利用小长方形的高度比为1:3:6:4:2得到分数在70.5~80.5范围内的人数的频率,然后用48乘以此组的频率得到该组的频数.
15. 20%
考点:频数(率)分布直方图
解:全班参赛人数为,3+6+7+6+11+12=45(人)
∴成绩不及格的百分率为945×100%=20%
分析:根据题意,计算得到参与调查的总人数,根据不及格的人数计算得到百分率即可。
三、综合题
16. (1)100
(2)55;10
(3)55100×80000=44000 (户)
∴估计该区居民用水量少于10吨的有44 000户.
考点:频数(率)分布直方图
解: :(1)20+35+20+15+5+5=100 (户)
∴这次一共抽查了100户;
(2)①20+35=55 (户),②5+5=10 (户)
∴用水量不足10吨的有55户,用水量超过16吨的有10户;
(3)55100×80000=44000 (户)
∴估计该区居民用水量少于10吨的有44 000户.
分析:(1)根据直方图,把用水量在各个段的户数加起来即可得到一共抽查的户数;
(2)根据直方图,把用水量不足10吨的户数加起来即可,把,用水量超过16吨的户数加起来即可;
(3)用该区居民用水量少于10吨的户数所占的百分比×80000,就可得出答案。
17. (1)45
(2)C
(3)解:补全的频数分布直方图如下图所示,
(4)解:200÷ 845 =1125(辆)?
答:当天的车流量约为1125辆.
考点:频数(率)分布直方图
解:(1)观察统计图知:车速在41千米/时到50千米/时的车辆数为10,占总数的 29 ,
所以,10÷ 29 =45;
故答案为:45;
( 2? )∵共45辆车,
∴中位数为第23辆车的速度,
∴50.5~60.5
故答案为:C.
分析:(1)用车速在41千米/时到50千米/时的车辆数除以 29 即可得到;
(2)根据车辆总数确定第23辆车为中位数,根据每一小组的频数确定中位数所处的小组即可;
(3)用总数减去其他小组的频数即可得到50.5~60.5小组的频数即可补全统计图;
(4)用200除以车速车速大于60千米/时的车辆所占的百分比即可求得车流量.
18. (1)13
(2)解:如图:
(3)108;27
考点:频数(率)分布直方图
解:(1)表中的m=40-4-8-12-3=13;(3)该年级跳绳不合格的人数约为360× 4+840=108 ,
成绩为优的人数约是360× 340=27 .
故答案是:108,27.
分析:(1)利用总数40减去其它组的频数即可求得;(2)根据(1)即可直接补全直方图;(3)利用总数360乘以对应的比例即可求解.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
