第一章三角形的初步知识（2）

三角形的初步知识（2）
复习目标：
了解全等三角形的概念，掌握两个三角形全等的条件，会在简单情况下判定两个三角形全等；
理解角平分线，线段的垂直平分线的概念，掌握和运用角平分线、线段的垂直平分线的性质进行简单说理和计算；
会用尺规作三角形、一个角的角平分线和线段的垂直平分线；
综合运用三角形全等知识解决实际问题；
复习过程：
知识整理
1.下列说法正确的是 （ ）
A．全等三角形是指形状相同的两个三角形； B．全等三角形是指面积相等的两个三角形
C．所有的等腰三角形都是全等三角形； D．所有等边三角形都是全等三角形
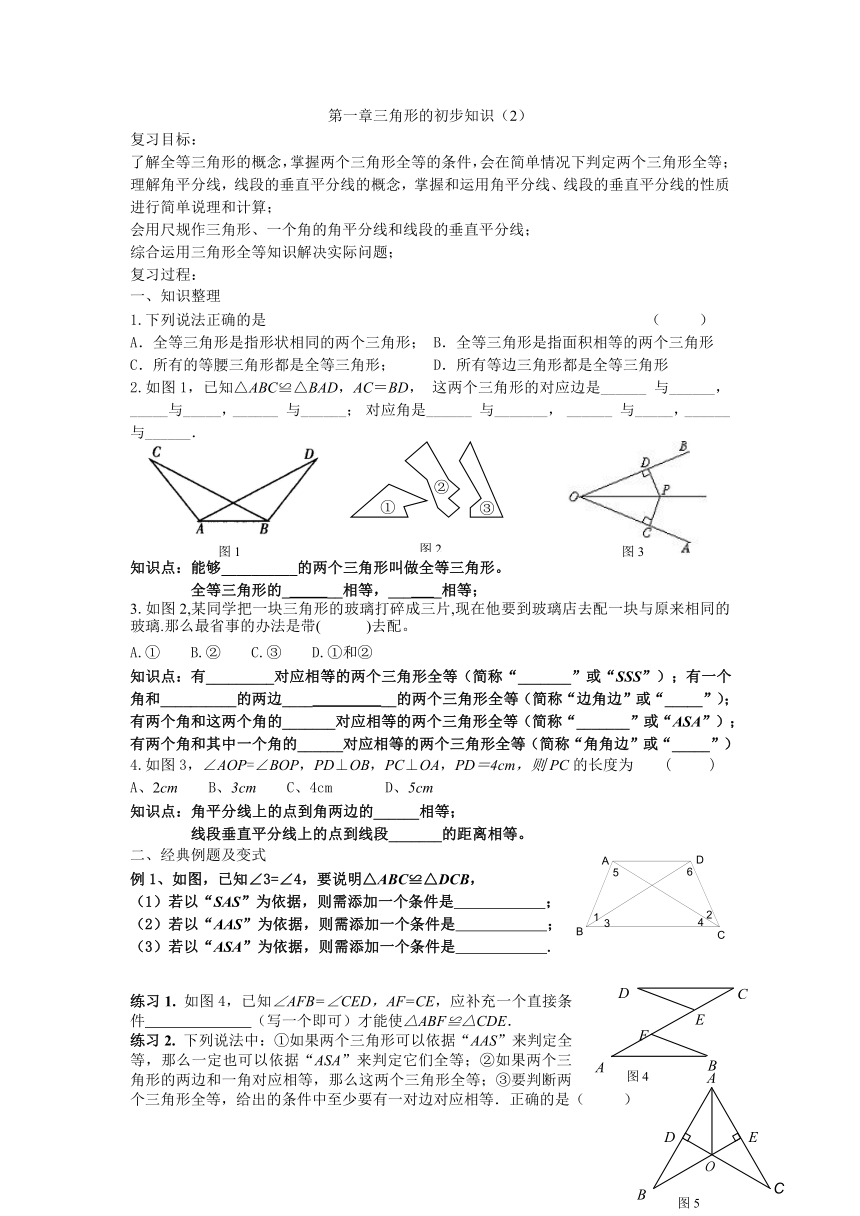
2.如图1，已知△ABC≌△BAD，AC＝BD，这两个三角形的对应边是______与______，_____与_____，______与______；对应角是______与_______，______与_____，______与______．
知识点：能够__________的两个三角形叫做全等三角形。
全等三角形的_ __相等，___ _相等；
3.如图2,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块与原来相同的玻璃.那么最省事的办法是带( )去配。
A.① B.② C.③ D.①和②
知识点：有_________对应相等的两个三角形全等（简称“_______”或“SSS”）；有一个角和__________的两边____ __的两个三角形全等（简称“边角边”或“_____”）；有两个角和这两个角的_______对应相等的两个三角形全等（简称“_______”或“ASA”）；有两个角和其中一个角的______对应相等的两个三角形全等（简称“角角边”或“_____”）
4.如图3，∠AOP=∠BOP，PD⊥OB，PC⊥OA，PD＝4cm，则PC的长度为 ( )
A、2cm B、3cm C、4cm D、5cm
知识点：角平分线上的点到角两边的______相等；
线段垂直平分线上的点到线段_______的距离相等。
经典例题及变式
例1、如图，已知∠3=∠4，要说明△ABC≌△DCB，
（1）若以“SAS”为依据，则需添加一个条件是 ；
（2）若以“AAS”为依据，则需添加一个条件是 ；
（3）若以“ASA”为依据，则需添加一个条件是 .
练习1. 如图4，已知∠AFB=∠CED，AF=CE，应补充一个直接条件 （写一个即可）才能使△ABF≌△CDE．
练习2. 下列说法中：①如果两个三角形可以依据“AAS”来判定全等，那么一定也可以依据“ASA”来判定它们全等；②如果两个三角形的两边和一角对应相等，那么这两个三角形全等；③要判断两个三角形全等，给出的条件中至少要有一对边对应相等．正确的是（ ）
A.①和② B.②和③ C.①和③ D.①②③
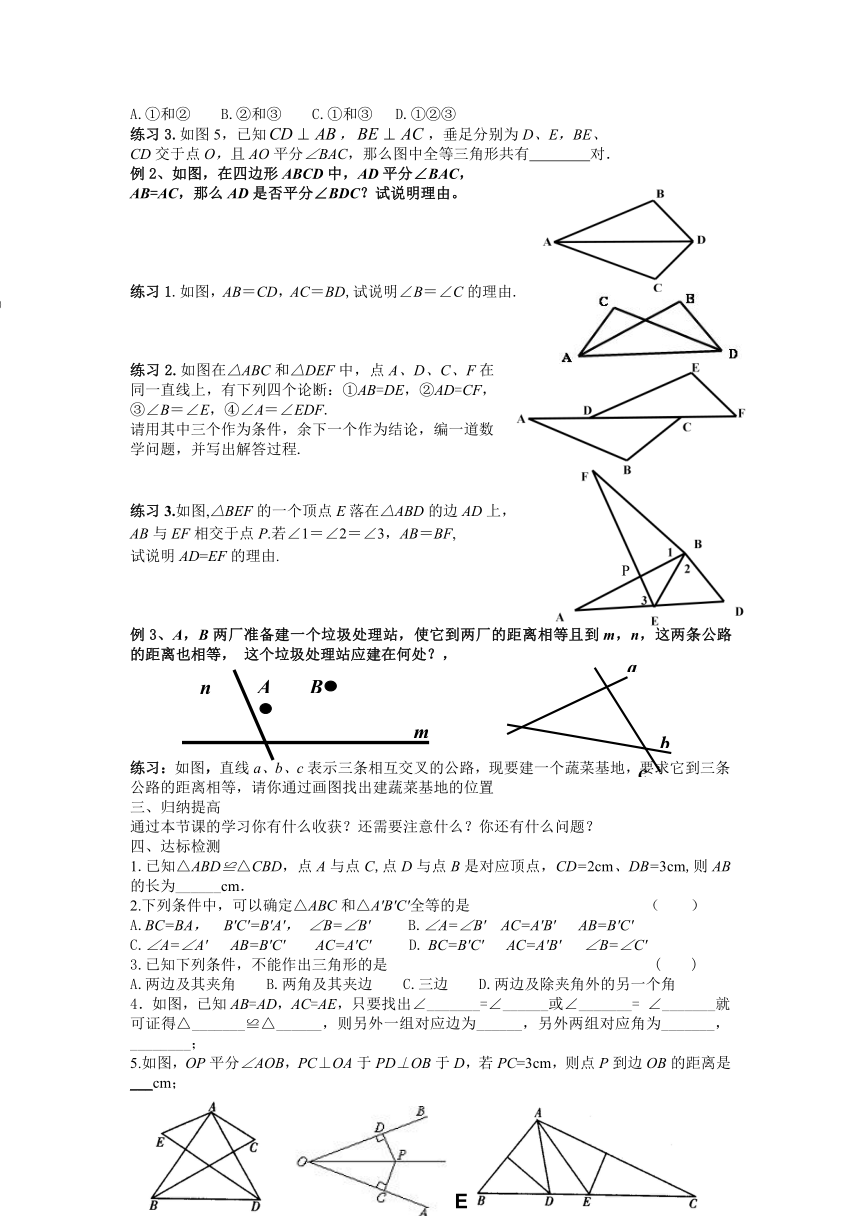
练习3.如图5，已知，，垂足分别为D、E，BE、
CD交于点O，且AO平分∠BAC，那么图中全等三角形共有　　　　对．
例2、如图，在四边形ABCD中，AD平分∠BAC，
AB=AC，那么AD是否平分∠BDC？试说明理由。
练习1.如图，AB＝CD，AC＝BD,试说明∠B＝∠C的理由.
练习2.如图在△ABC和△DEF中，点A、D、C、F在同一直线上，有下列四个论断：①AB=DE，②AD=CF，③∠B＝∠E，④∠A＝∠EDF.
请用其中三个作为条件，余下一个作为结论，编一道数学问题，并写出解答过程.
练习3.如图,△BEF的一个顶点E落在△ABD的边AD上，
AB与EF相交于点P.若∠1＝∠2＝∠3，AB＝BF,
试说明AD=EF的理由.
例3、A，B两厂准备建一个垃圾处理站，使它到两厂的距离相等且到m，n，这两条公路的距离也相等， 这个垃圾处理站应建在何处？，
练习：如图，直线a、b、c表示三条相互交叉的公路，现要建一个蔬菜基地，要求它到三条公路的距离相等，请你通过画图找出建蔬菜基地的位置
三、归纳提高
通过本节课的学习你有什么收获？还需要注意什么？你还有什么问题？
四、达标检测
1.已知△ABD≌△CBD，点A与点C,点D与点B是对应顶点，CD=2cm、DB=3cm,则AB的长为______cm．
2.下列条件中，可以确定△ABC和△A′B′C′全等的是 （ ）
A.BC=BA， B′C′=B′A′， ∠B=∠B′ B.∠A=∠B′ AC=A′B′ AB=B′C′
C.∠A=∠A′ AB=B′C′ AC=A′C′ D. BC=B′C′ AC=A′B′ ∠B=∠C′
3.已知下列条件，不能作出三角形的是 ( )
A.两边及其夹角 B.两角及其夹边 C.三边 D.两边及除夹角外的另一个角
4．如图，已知AB=AD，AC=AE，只要找出∠_______=∠______或∠_______=∠_______就可证得△_______≌△______，则另外一组对应边为______，另外两组对应角为_______，________；
5.如图，OP平分∠AOB，PC⊥OA于PD⊥OB于D，若PC=3cm，则点P到边OB的距离是 ___cm；
△6．如图，△ABC的两边AB和AC的垂直平分线分别交BC于D、E，若边BC长为8cm,
则△ADE的周长为 （ ）
A．不能确定 B．8cm C．16cm D．4cm
7.如图，已知△ACF≌△DBE，∠E=∠F，AD=9cm，BC=5cm，求AB的长．
8．为测量出池塘两端点A、B的距离，小明在地面上选择三个点O、D、C，使OA=OC，OB=OD,且点A，O，C和点B，O，D都在一条直线上，小明认为只要量出DC的距离，就能知道AB的距离，你认为小明的做法正确吗？请说明理由。
9．已知：如图，点D、E在△ABC的边BC上，AD＝AE，BD＝EC，
说明AB＝AC的理由.
10.如图，CD⊥AB于点D，BE⊥AC于点E，BE，CD交于点O，且AO平分∠BAC,则OB与OC相等吗？请说明理由.
11.如图,已知D、E两点分别在AC、AB上，且∠B=∠C，AB=AC，BD、EC交与点O,请找出图中所有的全等三角形，并说明理由.
△12．如图，在△ABC中，AD⊥BC，AD=BD，DE=DC，延长BE交AC于F，
（1）试说明△BDE≌△ADC的理由；
（2）你能说出BF⊥AC的理由吗？
五、延伸提高
△1．如图，已知△ABC和△DEC都是等边三角形，B、C、E在同一直线上，连结BD和AE.， 说明BD=AE的理由。
△2．如图，已知：AC⊥CD,BD⊥CD,M是AB的中点,连接CM并延长交BD于F,请说明M是CF的中点的理由.
☆3. 如图，已知AB=CD=AE=BC+DE=2．∠ABC=∠AED=90°，
求五边形ABCDE的面积．
①
③
②
图2
图1
图3
A
B
C
D
E
F
图4
A
D
B
Ｏ
C
E
图5
图①
A
P
m
B
A
n
a
b
c
E
C
B
A
第6小题
第5小题
第4小题
A
E
D
C
B
B D C
A
E
F