第一章三角形的初步知识(1)

第一章三角形的初步知识（1）
复习目标：
1.了解三角形的有关概念，会用符号和字母表示三角形，了解三角形的分类。
2.理解“三角形的任何两边之和大于第三边”的性质，能判断三条线段能否构成三角形。
3.理解三角形内角和外角的性质，会用这些性质解决有关角度的比较和计算的一些简单问题
4.了解三角形的中线、角平分线和高的概念，会用作图工具画三角形的中线、角平分线和高，会运用三角形的中线、角平分线和高的概念解决关于线段和角度计算的一些简单问题。
复习过程：
知识整理
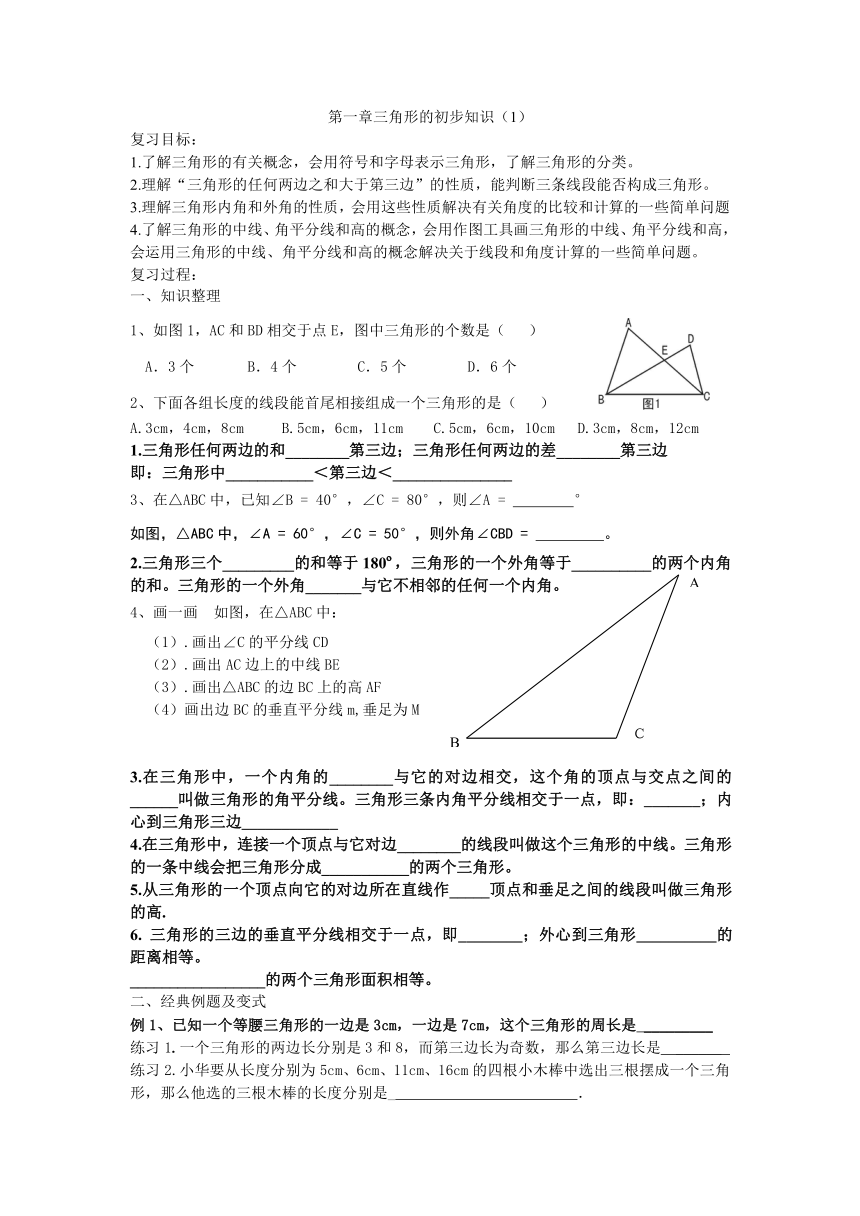
1、如图1，AC和BD相交于点E，图中三角形的个数是（ ）
A．3个 B．4个 C．5个 D．6个
2、下面各组长度的线段能首尾相接组成一个三角形的是（ ）
A.3cm，4cm，8cm B.5cm，6cm，11cm C.5cm，6cm，10cm D.3cm，8cm，12cm
1.三角形任何两边的和________第三边；三角形任何两边的差________第三边
即：三角形中___________＜第三边＜_______________
3、在△ABC中，已知∠B = 40°，∠C = 80°，则∠A = °
如图，△ABC中，∠A = 60°，∠C = 50°，则外角∠CBD = 。
2.三角形三个_________的和等于180 ，三角形的一个外角等于__________的两个内角的和。三角形的一个外角_______与它不相邻的任何一个内角。
4、画一画 如图，在△ABC中：
（1）.画出∠C的平分线CD
（2）.画出AC边上的中线BE
（3）.画出△ABC的边BC上的高AF
（4）画出边BC的垂直平分线m,垂足为M
3.在三角形中，一个内角的________与它的对边相交，这个角的顶点与交点之间的______叫做三角形的角平分线。三角形三条内角平分线相交于一点，即：_______；内心到三角形三边____________
4.在三角形中，连接一个顶点与它对边________的线段叫做这个三角形的中线。三角形的一条中线会把三角形分成___________的两个三角形。
5.从三角形的一个顶点向它的对边所在直线作_____顶点和垂足之间的线段叫做三角形的高.
6. 三角形的三边的垂直平分线相交于一点，即________；外心到三角形__________的距离相等。
_________________的两个三角形面积相等。
经典例题及变式
例1、已知一个等腰三角形的一边是3cm，一边是7cm，这个三角形的周长是 _________
练习1.一个三角形的两边长分别是3和8，而第三边长为奇数，那么第三边长是 ______
练习2.小华要从长度分别为5cm、6cm、11cm、16cm的四根小木棒中选出三根摆成一个三角形，那么他选的三根木棒的长度分别是_ ．
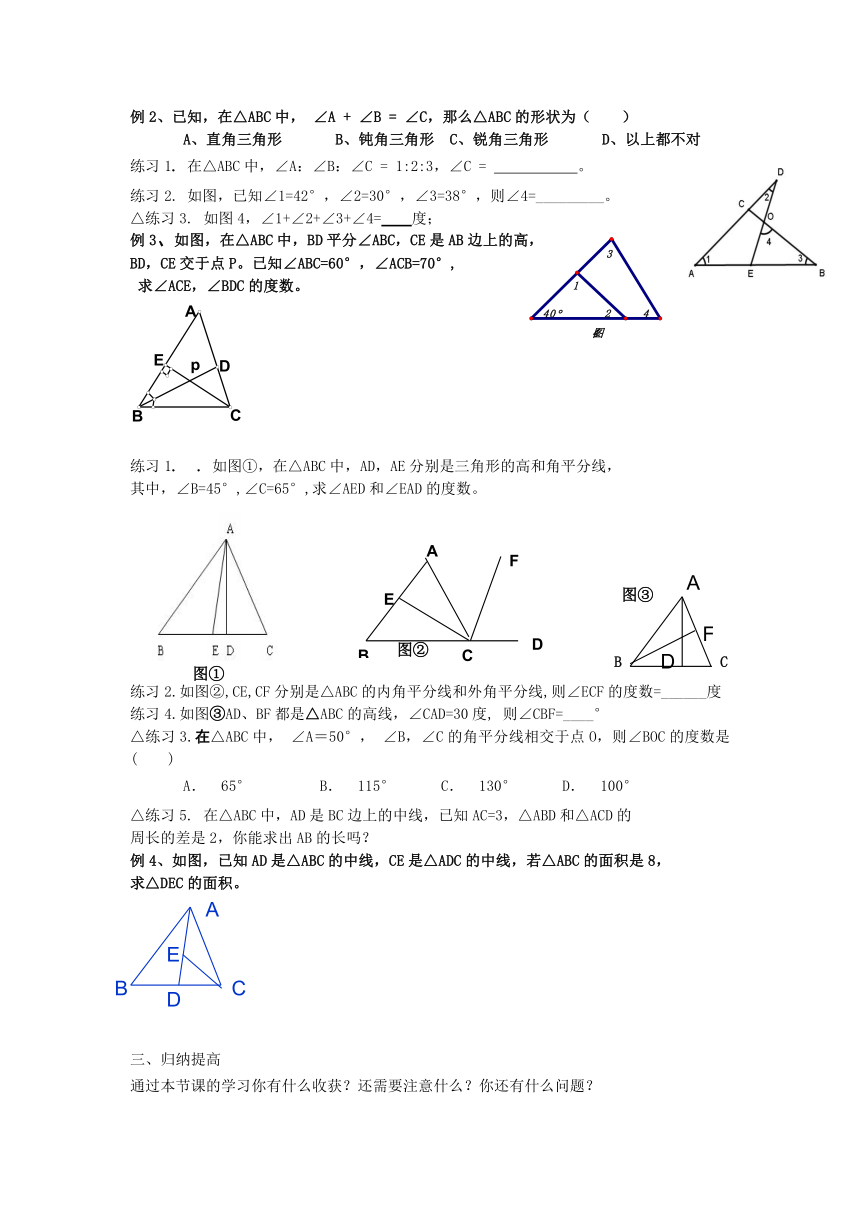
例2、已知，在△ABC中， ∠A + ∠B = ∠C，那么△ABC的形状为（ ）
A、直角三角形 B、钝角三角形 C、锐角三角形 D、以上都不对
练习1. 在△ABC中，∠A：∠B：∠C = 1:2:3，∠C = 。
练习2. 如图，已知∠1=42°，∠2=30°，∠3=38°，则∠4=_________。
△练习3. 如图4，∠1+∠2+∠3+∠4= 度；
例3、如图，在△ABC中，BD平分∠ABC，CE是AB边上的高，
BD，CE交于点P。已知∠ABC=60°，∠ACB=70°,
求∠ACE，∠BDC的度数。
练习1. . 如图①，在△ABC中，AD，AE分别是三角形的高和角平分线，
其中，∠B=45°,∠C=65°,求∠AED和∠EAD的度数。
B C
练习2.如图②,CE,CF分别是△ABC的内角平分线和外角平分线,则∠ECF的度数=______度
练习4.如图③AD、BF都是△ABC的高线，∠CAD=30度, 则∠CBF=____°
△练习3.在△ABC中， ∠A＝50°， ∠B，∠C的角平分线相交于点O，则∠BOC的度数是( )
A． 65° B． 115° C． 130° D． 100°
△练习5. 在△ABC中，AD是BC边上的中线，已知AC=3，△ABD和△ACD的
周长的差是2，你能求出AB的长吗？
例4、如图，已知AD是△ABC的中线，CE是△ADC的中线，若△ABC的面积是8，
求△DEC的面积。
归纳提高
通过本节课的学习你有什么收获？还需要注意什么？你还有什么问题？
四、达标检测
1.长度分别等于各组数据的三条线段中，能组成三角形的是（ ）
（A）5cm 3cm 9cm （B）5cm 3cm 7cm
（C）6cm 4cm 2cm （D）3cm 7cm 3cm
2．下列说法正确的是（ ）
（A）三角形的中线就是过顶点平分对边的直线
（B）三角形的三条角平分线的交点有可能在三角形外部
（C）三角形的三条高线的交点必在三角形内部
（D）以上说法都错
3．如图，AD是 ABC的一条中线，E是AD的中点，若 ABE的面积等于2，则 ABC的面积等于（ ）
（A）6 （B）8 （C）10 （D）无法确定
4．到三角形三边距离相等的点是（ ）
（A）三角形三条中线的交点 （B）三角形三条高线的交点
（C）三角形三条角平分线的交点 （D）三边中垂线的交点
5．如图，三角形个数共有几个（ ）
（A）6个　　 （B）8个　　 （C）10个　　 （D）12个
6．对于任意一个三角形，下列判断错误的是（ ）
（A）至少有一个角不大于60° （B）至少有两个角是锐角
（C）至多有一个角是直角 （D）至少有一个角大于60°
7．自行车的两个轮胎和支撑脚能停稳一辆自行车，这是利用了三角形的 ．
8．在直角三角形中，有一个锐角是54°，则另一个锐角是_______________．
9．在△ABC中，有两条边长分别是2 cm ，5 cm，则第三边的范围是_____________．若三边中有两边相等，则△ABC的周长为 cm．
10．如图6，AD是△ABC的 边BC上的高，已知AB=5 cm，
BC=2 cm，AD=3 cm，则△ABC的面积是 cm 2
11．如图，在 ABC中，AD是BC边上的中线，已知AB=7 cm ，AC=5cm，
则 ABD和 ACD的周长差为 cm．
12．已知三角形的三边长分别是3、x、9，则化简= ；
13．如图，CD是△ABC的角平分线，
已知∠A=70。，∠Ｂ=40。,求∠ACD与∠BDC的度数.
△14．如图，在△ABC中，AE是BC边上的高，AD是角平分线，∠B=42°，∠C=68°．
求∠DAE的度数；②若∠B=，∠C=，用含的代数式表示∠DAE．
五、延伸提高
△1．在△ABC中，∠A=2∠B=4∠C，则△ABC为（ ）
（A）锐角三角形 （B）钝角三角形 （C）直角三角形 （D）都有可能
☆2.如图，D是BC的中点，E在AC上且AE=2EC.AD与BE交与点O，已知△ABC的面积是12，
则S△AOE－S△BOD=________________
3. 已知等腰三角形的周长是25，一腰上的中线把三角形分成两个，两个三角形的
周长的差是4。求等腰三角形各边的长。
☆18．如图甲， ABC的两条角平分线BD，CE相交于P，
（1）已知∠A = 60°，则∠BPC = ___________；
（2）设∠A =α°，则用α的代数式表示∠BPC的度数是 ___________；
（3）如果将图甲中的BD，CE改为 ABC的外角∠CBD，∠ECB的平分线BP和CP，如图乙，若∠A =α°则用α的代数式表示∠BPC的度数是_____________；
（4）如果将图甲变为图丙，即∠ABC的平分线与∠ACF的平分线相交于点P ，∠A =α，则用α的代数式表示∠P的度数是_______________．
甲 乙 丙
B
A
Ｃ
图③
D
A
A
图①
B
C
D
F
E
图②
F
A
B
C
D
E
第5题
D
CC
B
A
E
第4题
A
B
C
D
第11题
A
B
C
D
E
A
B
C
D
第2题
E
A
B
C
D
E
P
A
E
D
C
B
P
A
B
C
P
F