4.3解二元一次方程组（2）

(共17张PPT)
主要步骤：
基本思路:
写
解
代
消去一个元
分别求出两个未知数的值
写出方程组的解
变
用一个未知数的代数式
表示另一个未知数
消元: 二元
1、解二元一次方程组的基本思路是什么？
2、用代入法解方程的步骤是什么？
一元
验
检验
怎样解下面的二元一次方程组呢？
①
②
小明
小彬
小丽
问题
过程
把②变形得：
代入①，不就消去
了！
小明
小明
小彬
小丽
问题
过程
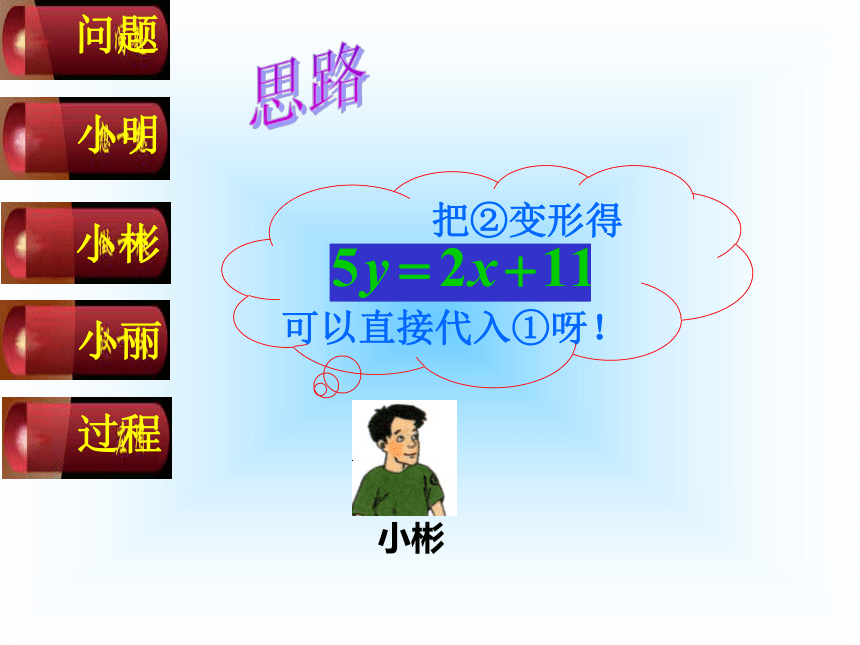
把②变形得
可以直接代入①呀！
小彬
小明
小彬
小丽
问题
过程
和
互为相反数……
按照小丽的思路，你能
消去一个未知数吗？
小丽
（3x ＋ 5y）+（2x － 5y）＝21 + (－11)
分析：
①
②
①左边 + ② 左边 = ① 右边 + ②右边
5x=10
小明
小彬
小丽
问题
过程
所以原方程组的解是
①
②
解:由①+②得: 5x=10
把x＝2代入①，得
x＝2
y＝3
参考小丽的思路，怎样解下面的二元一次方程组呢？
观察方程组中的两个方程，未知数x的系数
相等，都是2．把这两个方程两边分别相减，
就可以消去未知数x，同样得到一个一元一
次方程．
①
②
分析：
所以原方程组的解是
①
②
解：把 ②－①得:8y＝－8
y＝－1
把y ＝－1代入①，得
2x－5╳（－1）＝7
解得:x＝1
指出下列方程组求解过程中有错误的步骤，并给予订正：
7x－4y＝4
5x－4y＝－4
解:①－②，得
　　2x＝4－4，
　　　x＝0
①
①
②
②
3x－4y＝14
5x＋4y＝2
解：①－②，得
　　－2x＝12
　　　x ＝－6
解:　①－②，得
　　2x＝4＋4，
　　　x＝4
解:　①＋②，得
　　8x＝16
　　　x ＝2
上面这些方程组的特点是什么
解这类方程组基本思路是什么？
主要步骤有哪些？
主要步骤：
特点:
基本思路:
写
解
加减
二元
一元
加减消元:
消去一个元
分别求出两个未知数的值
写出原方程组的解
同一个未知数的系数相同或互为相反数
验
检验
例 用加减法解方程组:
对于当方程组中两方程不具备上述特点时，必须用等式性质来改变方程组中方程的形式，即得到与原方程组同解的且某未知数系数的绝对值相等的新的方程组，从而为加减消元法解方程组创造条件．
①×3得
所以原方程组的解是
①
②
分析：
③-④得: y=2
把y ＝2代入①，
解得: x＝3
②×2得
6x+9y=36 ③
6x+8y=34 ④
解：
1、解方程组
2、关于x、y的二元一次方程组
，求a、b的值
四. 方程组的应用
（1）
3x2a+b+2
+5y3a-b+1=8
是关于x、y的二元一次方程
求a、b
解：根据题意：得
2a+b+2=1
3a-b+1=1
得：
a=
b=
1
5
-
3
5
-
(2)已知3a3xb2x-y和-7a8-yb7是同类项
求x·y
解：根据题意：得
3x=8-y
2x-y=7
转化为
3x+y=8
2x-y=7
x=3
y=-1
∴
∴xy=-3
已知（3m+2n-16)2与|3m-n-1|互为相反数
求：m+n的值
解：根据题意：得
3m+2n-16=0
3m-n-1=0
解得：
m=2
n=5
∴m+n=7
谈谈你对解二元一次方程组的认识
请同学们归纳一下：
什么样的方程组用“代入法”？
什么样的方程组用“加减法”？
二元一次方程
一元一次方程
消元
转化