浙教版七年级下册第二章 二元一次方程组复习课(23张ppt)
文档属性
| 名称 | 浙教版七年级下册第二章 二元一次方程组复习课(23张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1015.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-07 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
一、二元一次方程组复习
有两个未知数且含未知数项的次数是一次的方程叫做二元一次方程。
1、什么是二元一次方程?
适合一个二元一次方程的一对未知数的值,叫做这个二元一次方程的一个解.
一般地,在二元一次方程组中,使每个方程都适合的解(公共解),叫做这个二元一次方程组的解。
2、什么是二元一次方程组?
有两个一次方程组成,并且含有
两个未知数的方程组
叫做二元一次方程组。
3、用代入法解二元一次方程组时,关键要确定先消哪一个未知数。
当方程组的两个方程中某一方程的未知数系数是1的绝对值时,则优先选择此方程,用含另一个未知数的代数式来表示它,再代入另一个方程求解。
在求出一个未知数的值后,再求另一个未知数的值,一般选择相对比较简单的一个方程来代,这样会使计算简便。
4、当方程组中两个方程的某个未知数
的系数相等或互为相反数时,
把方程的两边分别相减或相加来消去这个未知数,得到一个一元一次方程。
当方程组中两个未知数系数的绝对值均不相等,可以把两个方程的两边各自乘以一个适当的数,使某一个未知数的绝对值相等。
1、方程x+2y=7在正整数范围内的解有(
)
A
1个
B
2个
C
3个
D
无数个
C
解后语:二元一次方程一般有无数个解,但它的解若受到限制往往是有限个解。
2、若x2m-1+5y3n-2m=7是二元一次方程,
则m=
,n=
,
1
1
解后语:二元一次方程要求含有未知数项的次数都是1,同时未知数项的系数不能为零。
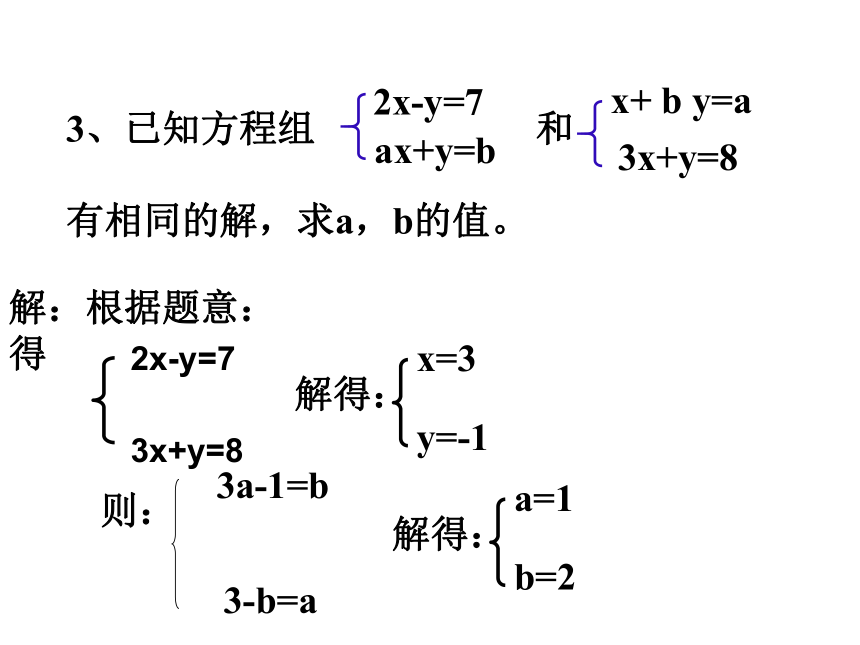
3、已知方程组
和
有相同的解,求a,b的值。
2x-y=7
ax+y=b
3x+y=8
x+
b
y=a
解:根据题意:得
2x-y=7
3x+y=8
解得:
x=3
y=-1
则:
3a-1=b
3-b=a
解得:
a=1
b=2
2x+1=5(y+2)
5(3x+2)-2(y+7x)=16
(1)
用适当的方法解下列方程组
3x-2y=16
(2)
已知(3m+2n-16)2与|3m-n-1|互为相反数
求:m+n的值
解:根据题意:得
3m+2n-16=0
3m-n-1=0
解得:
m=2
n=5
即:m+n=7
用适当的方法解下列方程组:
(1)
(2)
已知
,则
?
①②
①-②得:
整体思想
5
-1
1.已知二元一次方程组
,
则
,
。
2.已知
,
则
。
16
3.在
中,把①代入②得:
①②
。
整体代入
4.已知
,则
。
6
实际问题
分析
转化
方程(组)
求解
检验
问题解决
生活问题数学化,数学问题生活化
二、方程的应用题复习
列一次方程(组)解应用题的步骤:
(
审题,寻找等量关系)
(设未知数,列方程组)
(解方程组)
(检验,答)
理解问题
制定计划
执行计划
回顾反思
(1)??
设甲数为x,乙数为y,则甲数的2倍与乙数的3倍的和为15,列出方程为????????????
(2)一只蝈蝈6条腿,一只蜘蛛8条腿,现有蝈蝈和蜘蛛共10只,共有68条,若设蝈蝈有x只,蜘蛛y只,则列出方程组为??????????
(3)甲、乙两人参加植树活动,两人共植树20棵,已知甲植树数是乙的1.5倍。如果设甲植树x棵,乙植树y棵,那么可以列方程组为_________
(4)A、B两地相距36千米,甲从A地步行到B地,乙从B地步行到A地,两人同时相向出发,4小时后两人相遇,6小时后,甲剩余的路程是乙剩余路程的2倍,求二人的速度?
解:设甲的速度为x
千米/小时,
乙的速度为y
千米/小时
4x+4y=36
36-6x=2(36-6y)
(5)某车间有90名工人,每人每天平均能生产螺栓15个或螺帽24个,要使一个螺栓配套两个螺帽,应如何分配工人才能使螺栓和螺帽刚好配套?设生产螺栓x人,生产螺帽y人,列方程组为(
)
A
B、
C、
D、
c
例1.?
某蔬菜公司收购到某种蔬菜140吨,准备加工后上市销售,该公司的加工能力是:每天可以精加工6吨或者粗加工16吨,现计划用15天完成加工任务,该公司应安排几天粗加工,几天精加工,才能按期完成任务?如果每吨蔬菜粗加工后的利润为1000元,精加工后2000元,那么照此安排,该公司出售这些加工后的蔬菜共可获利多少元?
解:设粗加工x天,精加工y天.
X
+
y
=15
16x+6y
=140
解得:
X=5
y=10
答:粗加工5天,精加工10天.
获利
:
1000X16X5+2000X6X10=80000+120000=200000元
例2.
某中学组织初一同学春游,原计划租用45座客车若干辆,但有15人没有座位;如果租用同样数量的60座客车,则多出一辆,且其余客车恰好全满.已知45座客车用租金为每辆220元,60座客车用租金为每辆300元,试问:
(1)初一年级人数是多少?原计划租用45座客车多少辆?(2)要使每个同学都有座位,怎样租用车辆更合算?
解:
(1)
设45座客车x辆,学生y
人。
45x+15=y
60(x-1)=y
解得:
x=5
y=240
(2)因为,220/45<
300/60,所以因尽可能租用45座的车
45+15=60,所以只需将原计划中的一辆45座车换成一辆60座的车即可共需:220X4+300=1180元.
1.
某工厂现有库存某种原料1200吨,可以用来生产A,B两种产品,每生产一吨A种产品需这种原料2.5吨,生产费用900元,每生产一吨B种产品需原料2吨,生产费用1000元,可用来生产这两种产品的资金为53万,问A,B两种产品各生产多少吨,才能使库存原料和资金恰好用完?
解:设A种产品x吨,B种产品y吨。
2.5x+2y=1200
900x+1000y=530000
2.
张师傅预定计划生产一批零件,若按原计划每天生产30个,则只能完成任务的4/5,现在每天生产40个,结果比预定期限提前1天,还多完成25个,问预期多少天完成?这批零件有多少个?
解:设预期x天,共有y个零件。
30x=
4
5
y
40(x-1)=y+25
3.甲、乙两班学生到集市上购买苹果,苹果的价格如下表所示.甲班分两次共购买苹果70kg(第二次多于第一次),共付出189元,而乙班则一次购买苹果70kg.(1)乙班比甲班少付出多少元?
(2)甲班第一次,第二次分别购买苹果多少千克?
购苹果数
不超过30kg
30kg以上但
不超过50kg
50kg以上
每千克价格
3元
2.5元
2元
一、二元一次方程组复习
有两个未知数且含未知数项的次数是一次的方程叫做二元一次方程。
1、什么是二元一次方程?
适合一个二元一次方程的一对未知数的值,叫做这个二元一次方程的一个解.
一般地,在二元一次方程组中,使每个方程都适合的解(公共解),叫做这个二元一次方程组的解。
2、什么是二元一次方程组?
有两个一次方程组成,并且含有
两个未知数的方程组
叫做二元一次方程组。
3、用代入法解二元一次方程组时,关键要确定先消哪一个未知数。
当方程组的两个方程中某一方程的未知数系数是1的绝对值时,则优先选择此方程,用含另一个未知数的代数式来表示它,再代入另一个方程求解。
在求出一个未知数的值后,再求另一个未知数的值,一般选择相对比较简单的一个方程来代,这样会使计算简便。
4、当方程组中两个方程的某个未知数
的系数相等或互为相反数时,
把方程的两边分别相减或相加来消去这个未知数,得到一个一元一次方程。
当方程组中两个未知数系数的绝对值均不相等,可以把两个方程的两边各自乘以一个适当的数,使某一个未知数的绝对值相等。
1、方程x+2y=7在正整数范围内的解有(
)
A
1个
B
2个
C
3个
D
无数个
C
解后语:二元一次方程一般有无数个解,但它的解若受到限制往往是有限个解。
2、若x2m-1+5y3n-2m=7是二元一次方程,
则m=
,n=
,
1
1
解后语:二元一次方程要求含有未知数项的次数都是1,同时未知数项的系数不能为零。
3、已知方程组
和
有相同的解,求a,b的值。
2x-y=7
ax+y=b
3x+y=8
x+
b
y=a
解:根据题意:得
2x-y=7
3x+y=8
解得:
x=3
y=-1
则:
3a-1=b
3-b=a
解得:
a=1
b=2
2x+1=5(y+2)
5(3x+2)-2(y+7x)=16
(1)
用适当的方法解下列方程组
3x-2y=16
(2)
已知(3m+2n-16)2与|3m-n-1|互为相反数
求:m+n的值
解:根据题意:得
3m+2n-16=0
3m-n-1=0
解得:
m=2
n=5
即:m+n=7
用适当的方法解下列方程组:
(1)
(2)
已知
,则
?
①②
①-②得:
整体思想
5
-1
1.已知二元一次方程组
,
则
,
。
2.已知
,
则
。
16
3.在
中,把①代入②得:
①②
。
整体代入
4.已知
,则
。
6
实际问题
分析
转化
方程(组)
求解
检验
问题解决
生活问题数学化,数学问题生活化
二、方程的应用题复习
列一次方程(组)解应用题的步骤:
(
审题,寻找等量关系)
(设未知数,列方程组)
(解方程组)
(检验,答)
理解问题
制定计划
执行计划
回顾反思
(1)??
设甲数为x,乙数为y,则甲数的2倍与乙数的3倍的和为15,列出方程为????????????
(2)一只蝈蝈6条腿,一只蜘蛛8条腿,现有蝈蝈和蜘蛛共10只,共有68条,若设蝈蝈有x只,蜘蛛y只,则列出方程组为??????????
(3)甲、乙两人参加植树活动,两人共植树20棵,已知甲植树数是乙的1.5倍。如果设甲植树x棵,乙植树y棵,那么可以列方程组为_________
(4)A、B两地相距36千米,甲从A地步行到B地,乙从B地步行到A地,两人同时相向出发,4小时后两人相遇,6小时后,甲剩余的路程是乙剩余路程的2倍,求二人的速度?
解:设甲的速度为x
千米/小时,
乙的速度为y
千米/小时
4x+4y=36
36-6x=2(36-6y)
(5)某车间有90名工人,每人每天平均能生产螺栓15个或螺帽24个,要使一个螺栓配套两个螺帽,应如何分配工人才能使螺栓和螺帽刚好配套?设生产螺栓x人,生产螺帽y人,列方程组为(
)
A
B、
C、
D、
c
例1.?
某蔬菜公司收购到某种蔬菜140吨,准备加工后上市销售,该公司的加工能力是:每天可以精加工6吨或者粗加工16吨,现计划用15天完成加工任务,该公司应安排几天粗加工,几天精加工,才能按期完成任务?如果每吨蔬菜粗加工后的利润为1000元,精加工后2000元,那么照此安排,该公司出售这些加工后的蔬菜共可获利多少元?
解:设粗加工x天,精加工y天.
X
+
y
=15
16x+6y
=140
解得:
X=5
y=10
答:粗加工5天,精加工10天.
获利
:
1000X16X5+2000X6X10=80000+120000=200000元
例2.
某中学组织初一同学春游,原计划租用45座客车若干辆,但有15人没有座位;如果租用同样数量的60座客车,则多出一辆,且其余客车恰好全满.已知45座客车用租金为每辆220元,60座客车用租金为每辆300元,试问:
(1)初一年级人数是多少?原计划租用45座客车多少辆?(2)要使每个同学都有座位,怎样租用车辆更合算?
解:
(1)
设45座客车x辆,学生y
人。
45x+15=y
60(x-1)=y
解得:
x=5
y=240
(2)因为,220/45<
300/60,所以因尽可能租用45座的车
45+15=60,所以只需将原计划中的一辆45座车换成一辆60座的车即可共需:220X4+300=1180元.
1.
某工厂现有库存某种原料1200吨,可以用来生产A,B两种产品,每生产一吨A种产品需这种原料2.5吨,生产费用900元,每生产一吨B种产品需原料2吨,生产费用1000元,可用来生产这两种产品的资金为53万,问A,B两种产品各生产多少吨,才能使库存原料和资金恰好用完?
解:设A种产品x吨,B种产品y吨。
2.5x+2y=1200
900x+1000y=530000
2.
张师傅预定计划生产一批零件,若按原计划每天生产30个,则只能完成任务的4/5,现在每天生产40个,结果比预定期限提前1天,还多完成25个,问预期多少天完成?这批零件有多少个?
解:设预期x天,共有y个零件。
30x=
4
5
y
40(x-1)=y+25
3.甲、乙两班学生到集市上购买苹果,苹果的价格如下表所示.甲班分两次共购买苹果70kg(第二次多于第一次),共付出189元,而乙班则一次购买苹果70kg.(1)乙班比甲班少付出多少元?
(2)甲班第一次,第二次分别购买苹果多少千克?
购苹果数
不超过30kg
30kg以上但
不超过50kg
50kg以上
每千克价格
3元
2.5元
2元
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
