《同底数幂的除法》课件1

(共11张PPT)
5.6
(一)
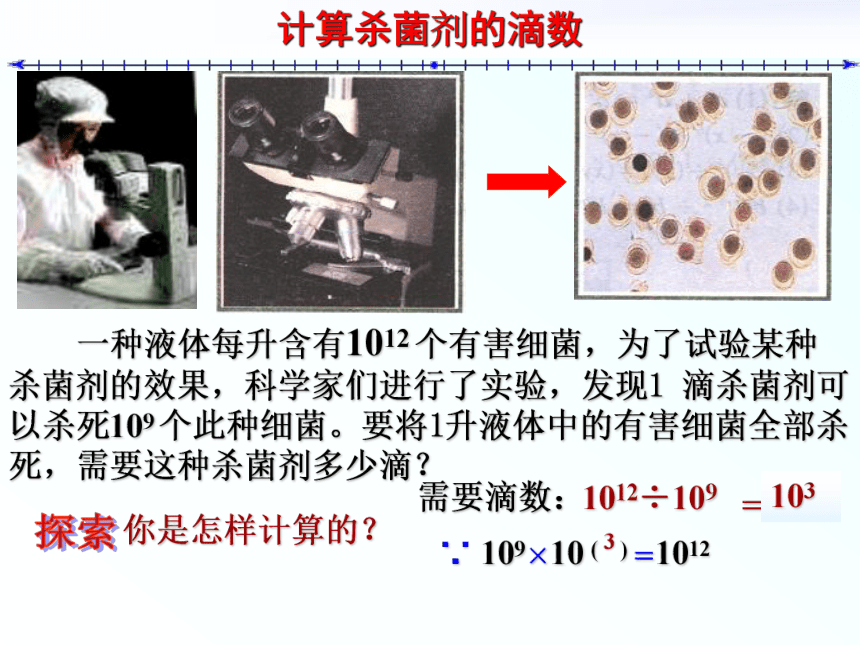
计算杀菌剂的滴数
一种液体每升含有1012 个有害细菌，为了试验某种杀菌剂的效果，科学家们进行了实验，发现1 滴杀菌剂可以杀死109 个此种细菌。要将1升液体中的有害细菌全部杀死，需要这种杀菌剂多少滴？
你是怎样计算的？
需要滴数：
∵ 109×10 ( ) =1012
=？
3
103
1012÷109
用 逆运算与同底数幂的乘法 来计算
计算下列各式：
（1）108 ÷105
（2）10m÷10n
（3）(–3)m÷(–3)n
做一做
3
解 :
(1) ∵ 105×10( ) =108,
∴108 ÷105 =
103 ;
m–n
(2) ∵ 10n×10( ) =10m,
∴10m ÷10n=
10m–n ;
(3) ∵ (–3)n×(–3)( ) =(–3)m,
∴ (–3)m ÷(–3) n=
m–n
(–3)m–n ;
猜想
am÷an=
=am–n
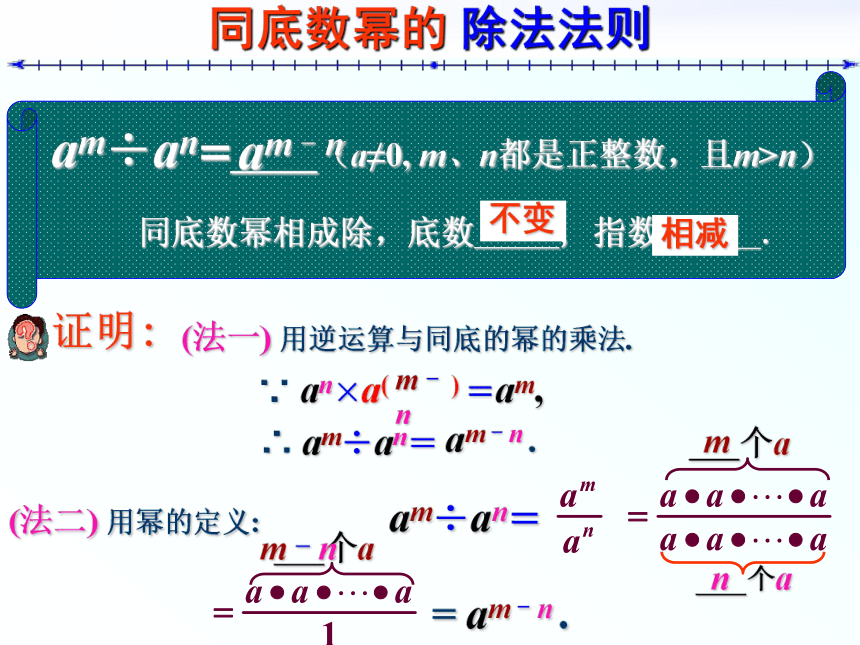
同底数幂的 除法法则
am÷an= （a≠0, m、n都是正整数，且m>n）
同底数幂相成除，底数_____, 指数______.
am–n
不变
相减
证明:
(法一) 用逆运算与同底的幂的乘法.
∵ an×a( ) =am,
∴ am÷an=
m–n
am–n .
(法二) 用幂的定义: am÷an=
个a
m
个a
n
个a
m–n
= am–n .
例题解析
【例1】计算：
(1) a7÷a4 ; (2) (-x)6÷(-x)3;
(3) (xy)4÷(xy) ; (4) b2m+2÷b2 .
= a7–4
= a3 ;
(1) a7÷a4
解：
(2) (-x)6÷(-x)3
= (-x)6–3
= (-x)3
(3) (xy)4÷(xy)
=(xy)4–1
(4) b2m+2÷b2
= b2m+2 – 2
阅读 体验
= -x3 ;
=(xy)3
=x3y3
= b2m .
注意

最后结果中幂的形式应是最简的.
① 幂的指数、底数都应是最简的；
② 幂的底数是积的形式时，要再用一次(ab)n=an an.
②底数中系数不能为负；
计算：（口答）
⑴ s9÷s3
⑵ (-3)6 ÷(-3)2
⑶ (ab)5÷(ab)
⑷ (x-y)8÷(x-y)3
⑸ (-t)11÷t2
⑹ (a-b)5÷(b-a)4
自我检测
1.下列计算对吗？
为什么？
错的请改正。
① a6÷a2 = a3
② s2÷s = s3
③(-c)4÷(-c)2 = -c2
④(-x)9÷(-x)9 = -1
⑴(-5)5÷(-5)3
⑵b2m+2÷b2
⑶(-ab)3÷(ab)2
⑷ a8÷a4·a4
⑸(-a-b)5÷(a+b)2
⑹y3÷(y2)3
⑺ 2×2n÷2n-1
（8）( a +b)6 ÷ ( a +b)4
拓 展 练 习
（1） x4n＋1÷x 2n－1·x2n＋1=
（2）已知ax=2 ay=3 则ax－y=
（3）已知ax=2 ay=3 则 a2x－y=
（4）已知am=4 an=5 求a3m－2n的值。
（5）若10a=20 10b=5，试求9a÷32b的值。
（6）已知2x－5y－4=0，求4x÷32y的值。
作业：
作业本
同步
教与学5.6