因式分解 复习课件

(共21张PPT)
因式分解
你能用几种不同的方法计算1002－992，哪种方法最简单？请与你的同伴交流。
1002－992
=（100+99）（100－99）
=199×1
=199
a2-b2=(a+b)(a-b)
=(a+b)2
=m(a+b)
(a+b)(a-b)
(a+b)2
m(a+b)
=a2-b2
=a2+2ab+b2
=am+bm
整式乘法
因式分解
整式的积
多项式
多项式
整式的积
a2+2ab+b2
am+bm
你能尝试把a2－b2写成整式的积的形式吗？
一般地，把一个多项式转化成几个整式的积的形式，叫做因式分解，有时我们也把这一过程叫做分解因式。
要点：１．变形对象：多项式
　　　２．由和的形式变成积的形式
　　　３．几个整式的积
（1）∵3a(a+4) =3a2+12a
∴ 3a2+12a = ( )( );
（2）∵ (a+3)2=a2+6a+9
∴a2+6a+9 = ( )( );
（3）∵(2－a)(2+a) = 4－a2
∴4－a2 = ( )( );
3a
a＋4
a＋3
a＋3
2－a
2＋a
（a＋3）2
因式分解与整式乘法有什么关系？
因式分解与整式乘法是互逆 过程
（1）
（2）
（3）
（4）
（5）
（6）
（7）
是
不是
不是
不是
不是
不是
不是
下列代数式从左到右的变形是因式分解吗？
例：检验下列因式分解是否正确：
（1）
（2）
（3）
（4）
(√)
(x)
(x)
(x)
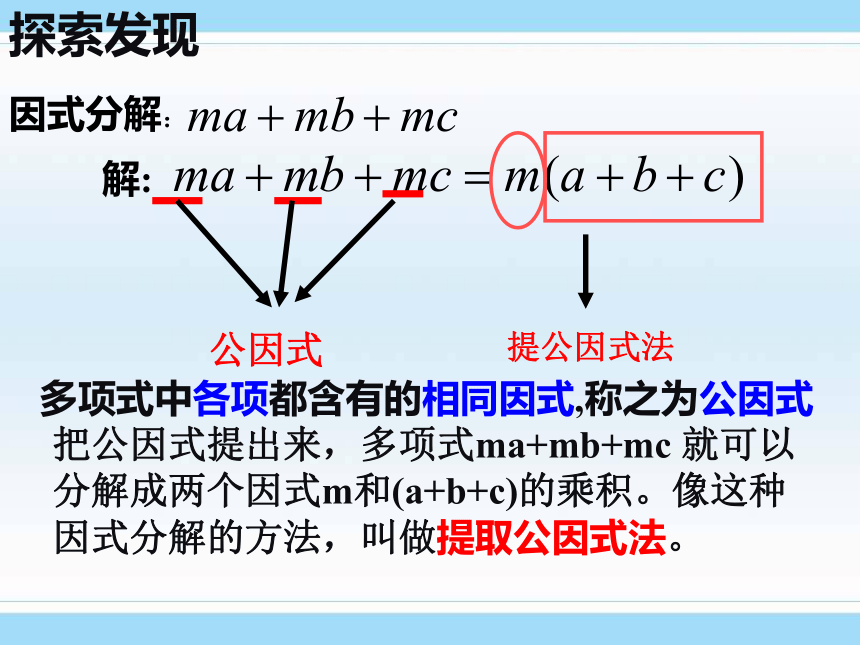
因式分解：
把公因式提出来，多项式ma+mb+mc 就可以分解成两个因式m和(a+b+c)的乘积。像这种因式分解的方法，叫做提取公因式法。
探索发现
解:
公因式
多项式中各项都含有的相同因式,称之为公因式
提公因式法
提取公因式法
应提取的公因式为:________
议一议：
多项式　　　　　　　　有公因式吗？是什么？
公因式的确定方法：
应提取的公因式的是：各项系数都是整数时,取
各项系数的最大公约数与各项都含有的相同字母的最低次数幂的积。
练一练：
多项式 公因式
因式分解结果
应提取的公因式的是：各项系数的最大公约数与各项都含有的相同字母的最低次数幂的积。
找出公因式
提取公因式得到 另一个因式
写成积的形式
←不能漏掉
=x(3x-6y+1)
原式=x(3x2 ÷x-6xy ÷x+x ÷x)
提取公因式法的一般步骤：
（1）确定应提取的公因式
（2）多项式除以公因式，所得的商作为另一个因式
（3）把多项式写成这两个因式的积的形式
（2）把 -24x3 –12x2 +28x 分解因式.
当多项式第一项系数是负数，通常先提出“-”号，使括号内第一项系数变为正数，注意括号内各项都要变号。
解：原式=
=
(24x3 ÷ 4x+12x2 ÷ 4x-28x ÷4x)
(6x2+3x-7)
练一练：分解因式
(3)若多项式-6ab+18abx+24aby的一个因式是-6ab，那么另一 个因式是（ ）
（A）-1-3x+4y （B）1+3x-4y
（C）-1-3x-4y （D）1-3x-4y
D
(4)若多项式(a+b)xy+(a+b)x要分解因式,则要提的公因式是 .
(a+b)x
例2：分解因式
括号前面是“+”号，括到括号里的各项都不变号；括号前面是“—”号，括到括号里的各项都变号。
添括号法则：
下面的分解因式对吗？如果不对，应怎样改正？
１．提公因式法
１）．确定应提取的公因式
　　　　　　　　２）．用公因式去除这个多项式，所得的商作
　　　　　　为另一个因式（为什么？）
　　　　　　　３）．把多项式写成这两个因式积的形式。
２．提取公因式的一般步骤：
当ｎ为奇数时
当ｎ为偶数时
３整体的思想