6.3用平方差公式分解因式

(共27张PPT)
§６.3用乘法公式分解因式（1）
运用平方差公式因式分解
同学们，让我们一起乘坐幸福
快车，领略一路的数学美景！
13.5cm
6.5cm
π.13.5
2
π.6.5
2
π
13.5
2
.
π
.
6.5
2
-
(若π取3）
3×13.5 - 3×6.5
2
2
你能不用计算器快速算出吗？
两者面积之差为（列出算式）：
=3×（13.52 － 6.52 ）
=3 ×20 ×7
=3 ×(13.5＋6.5) (13.5 － 6.5)
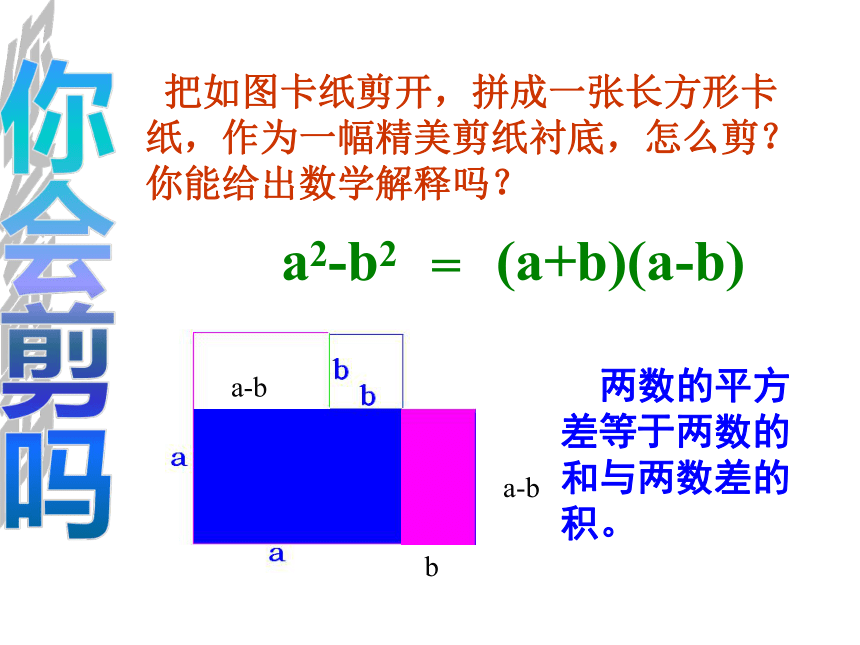
把如图卡纸剪开，拼成一张长方形卡纸，作为一幅精美剪纸衬底，怎么剪？你能给出数学解释吗？
a-b
a-b
b
a-b
a2-b2
(a+b)(a-b)
=
两数的平方差等于两数的和与两数差的积。
)
)(
(
b
a
b
a
-
+
=
2
2
b
a
-
)
)(
(
2
2
b
a
b
a
b
a
-
+
=
-
整式乘法
因式分解
两个数的和与两个数的差的乘积，等于这两个数的平方差。
两个数的平方差，等于这两个数的和与这两个数的差的乘积.
平方差公式：
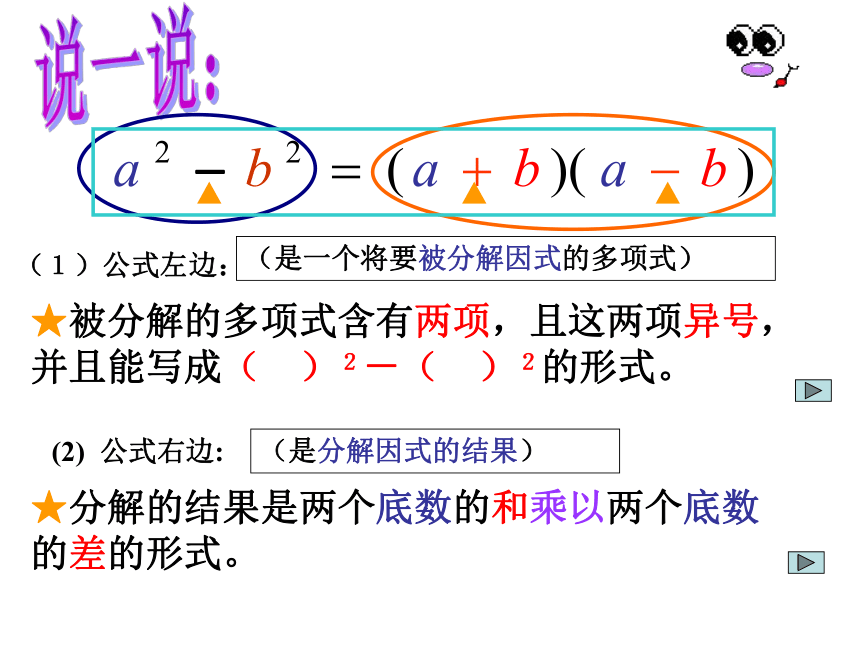
（１）公式左边：
（是一个将要被分解因式的多项式）
★被分解的多项式含有两项，且这两项异号，并且能写成（　）２－（　）２的形式。
(2) 公式右边:
（是分解因式的结果）
★分解的结果是两个底数的和乘以两个底数的差的形式。
)
)(
(
2
2
b
a
b
a
b
a
-
+
=
-
▲
▲
▲
a2-b2=(a + b)(a - b)
例：
16a2-1
=(4a)2-12
=(4a+1)(4a-1)
下列多项式能否用平方差公式分解因式？说说你的理由。
（1）4x2+y2 (2) 4x2-(-y)2
(3) -4x2-y2 (4) -4x2+y2
(5) a2-4 (6) a2+3
能用平方差公式分解因式的多项式的特征：
1、由两部分组成；
2、两部分符号相反；
3、每部分都能写成某个式子的平方。
能
能
能
不能
不能
不能
运用a2-b2=(a+ b)(a- b)
例1:把下列各式分解因式：
解:（1）原式=（2p)2-(mn)2
= (2p+mn)(2p-mn)
说明:公式中的a、b可以是单项式(数字、字母)、还可以是多项式.分解因式最后结果中如果有同类项，一定要合并同类项。
（3）原式 =[(x+z)+(y+z)][(x+z)- (y+z)]
=(x+y+2z)(x-y)
=(x+z+y+z)(x+z- y-z)
(1)-m2n2+4p2 (2) x2 - y2 (3)(x+z)2-(y+z)2
（2）原式 =( x)2 –( y)2
=( x+ y)( x- y)
1.判断下列利用平方差公式分解因式是否正确,不对,请改正
(3) -9+4x2=(2x-3)(2x+3)
(2) -a4+b2=(a2+b)(a2-b)
(5) a2-(b+c)2=(a+b+c)(a-b+c)
(6) s2-t2=(-s+t)(-s-t)
×
×
(b+a2)(b-a2)
(a+b+c)(a-b-c)
√
√
(s-t)(s+t)
a2-b2=(a+b)(a-b)
=
=[-(s-t)][-(s+t)]
(4) -1-x2=(1-x)(1+x)
(1) x2-4y2=(x+4y)(x-4y)
×
×
(x+2y)(x-2y)
不能分解因式
判断
=(4x+y) (4x －y)
=(2x + y) (2x － y)
3
1
3
1
=(2k+5mn) (2k －5mn)
2.把下列各式分解因式：
a2 － b2= (a ＋ b) (a － b)
看谁快又对
= (a+8) (a －8)
（1）a2－64
1
（2）16x2 －y2
2
(3) － y2 + 4x2
9
1
3
(4) 4k2 －25m2n2
4
参照对象：
)
)(
(
2
2
b
a
b
a
b
a
-
+
=
-
20062－20052 =
（2mn）2 - ( 3xy)2 =
(x+z)2 - (y+z)2 =
结论：
公式中的a、b无论表示数、单项式、还是多项式，只要被分解的多项式能转化成平方差的形式，就能用平方差公式因式分解。
ma+mb=m(a+b) m是各项的公因式
a2-b2=(a+b)(a-b)
合作学习
例2. 分解因式4x3y-9xy3
(2)提取公因式后,多项式还能继续分解因式吗
4x3y-9xy3=xy(4x2-9y2)
4x3y-9xy3=xy (4x2-9y2)=xy(2x+3y)(2x-3y)
(1)能分解因式吗 用什么方法
[注意]: 1.一般地,因式分解时有公因式先提公因式
2.因式分解时要分解彻底。
正确率+速度=效率
(2) 0.01s2-t2
(1) 16-a2
(4) -1+9x2
(5) (a-b)2-(c-b)2
(6) -(x+y)2+(x-2y)2
解:原式=(4+a)(4-a)
解:原式=(0.1s+t)(0.1s-t)
解:原式=(3x-1)(3x+1)
解:原式=(a-c)(a+c+2b)
解:原式=-3y(2x-y)
a2-b2=(a+b)(a-b)
平方差公式:a2-b2 =(a+b)(a-b)
把下列各式分解因式
① x4 - 81y4 ② 2a - 8a
1.解:原式= (x + 9y ) (x - 9y )
= (x + 9y ) (x+ 3y) (x- 3y)
2.解:原式=2a(a2- 4)
=2a(a+2)(a-2)
(1)能提取公因式。
993-99 =99(992-1)
（2）还能继续分解
993-99=99(99+1)(99-1)
=99x100x98
解： 4x3y-9xy3
=xy(4x2-9y2)
1、请问993-99能被100整除？温馨提示：（1）能否提取公因式？（2）提取公因式后，还能 继续分解因式吗？
2、怎样把多项式4x3y-9xy3分解因式？
=xy[(2x)2-(3y)2]
=xy(2x+3y)(2x-3y)
结论：
993-99能被100整除。
记得要提取公因式！
1、分解因式
4x2–y2=(4x+y)(4x-y )
诊断分析：
公式理解不准确，不能很好的把握公式中的项， 4x2–y2中4x2 相当于a2 ,则2x相当于“a”.
2、分解因式
x4–y4=(x2+y2)(x2–y2)
(4a+5b)2–(2a-b)2=(6a+4b)(2a+6b)
诊断分析：
综合运用提取公因式，公式法公解因式时，提公因式后，另一个因式还可以继续分解，同学们千万要注意分解完毕后对结果进行检查，看是否分解彻底了。
正确分解：
4x2–y2=(2x+y)(2x-y )
= (x2+y2) (x+y)(x-y )
问题在哪里？
=4 (3a+2b)(a+3b)
补充分解：
通过本节课的学习,你有哪些收获
分解因式的步骤：
(1)优先考虑提取公因式法
(2)其次看是否能用公式法 （如平方差公式）
(3)务必检查是否分解彻底了
1、作业本6.3
2、课内作业
作业：
1.分解因式：
（1）4x3-x
( 2 ) a4-81
（3）(3x－4y）2－（4x+3y）2
（4）16（3m－2n）2－25（m－n）2

2、计算
（1）9992－9982
（2）25 × 2652－1352 × 25
3、若n为整数，则（2n＋1)2－(2n－1)2能被
8整除吗 请说明理由.
4. 运用本节所学的知识，把9991分解成两个
整数的积.
5、计算 (1－ 1/22 ) ·(1 －1/32 ) ·(1 －1/42) …
(1 －1/20052 ) ·(1 －1/20062 )的值,
从中你可以发现什么规律
b米
b米
a米
(a-2b)米
(a+2b)米
a 米
从前有一位张老汉向地主租了一块 “十字型”土地（尺寸如图）。为便于种植，他想换一块相同面积的长方形土地。 同学们，你能帮助张老汉算出这块长方形土地的长和宽吗？
在日常生活中如上网等都需要密码.
有一种因式分解法产生的密码方便记忆又不易破译.
例如用多项式x4-y4因式分解的结果来设置密码, 当取x=9,y=9时,可得一个六位数的密码“018162”.你想知道这是怎么来的吗
小明选用多项式4x3-xy2，取x=10,y=10时。用上述方法产生的密码是什么 (写出一个即可)
杭州湾跨海大桥打下的一根用特殊材料制成的桩管
(横截面如图所示),它的外半径为R米,内半径为r米.已知外半径与内半径和为2米,外半径与内半径差为0.3米,
求横截面面积(结果保留 )
R
r
英国数学家狄摩根在青年时代,曾有人他:“今年多大年龄？”狄摩根想了想说：“今年，我的年龄和我弟弟年龄的平方差是141，你能算出我的年龄和我弟弟的年龄吗？”假设狄摩根的年龄为x岁，他弟弟的年龄为 y岁，你能算出他们的年龄吗？