6.3用完全平方公式分解因式

(共28张PPT)
把下列各式分解因式
首项有负常提负
各项有公先提公
分解因式要彻底
（1） － ax4+ax2
（2）16m4－n4
a2 b2 = (a+b)(a b)
把下列多项式因式分解：
a
a
b
b
甲
乙
乙
丙
丁
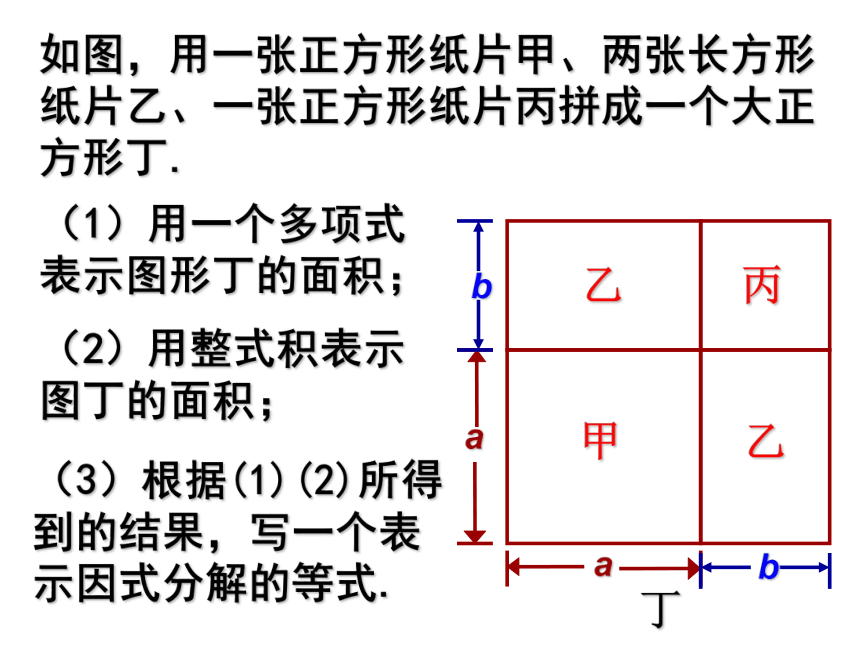
如图，用一张正方形纸片甲、两张长方形纸片乙、一张正方形纸片丙拼成一个大正方形丁.
（1）用一个多项式表示图形丁的面积；
（2）用整式积表示图丁的面积；
（3）根据(1)(2)所得到的结果，写一个表示因式分解的等式.
两数的平方和，加上这两数的积的2倍，等于这两个数和的平方.
形如 的多项式，叫做完全平方式.
用完全平方公式分解因式的关键是：判断这个多项式是不是一个完全平方式.
完全平方式特征：
（1）多项式有3项；
（2）其中两项为平方项（两数的平方和），另一项为中间项（这两数积的2倍）.
先确定平方项，再检查剩余项是否符合两数积的2倍（中间项）.
判断方法：
现在我们把完全平方公式反过来，可得：
两个数的平方和，加上 这两个数的积的两倍，等于这两数和 的平方．
完全平方公式：
（或减去）
（或者差）
两个数的平方和，加上（或减去）这两个数的积的两倍，等于这两数和（或者差）的平方．
形如 　 的多项式称为完全平方式.
形如 或
的多项式,叫做完全平方式。
平方差公式法和完全平方公式法统称公式法。
平方差公式法：适用于平方差形式的多项式
完全平方公式法：适用于完全平方式
判别下列各式是不是完全平方式
是
是
是
是
1．判别下列各式是不是完全平方式．
不是
是
是
不是
是
2.填写下表（若某一栏不适用，请填入“不适用”）
a表示x,b表示3
a，b各表示什么
表示成（a＋b)2或（a－b)2的形式
是
是否是完全平方式
多项式
是
a表示2y,b表示1
不是
不适用
不适用
不适用
不适用
不是
是
a表示1,b表示
是
a表示2y,b表示3x
3.按照完全平方公式填空：
4.请补上一项，使下列多项式成为完全平方式．
例1 把下列各式分解因式:
解: (1)原式
=(2a)2+
2 2a 3b+
(3b)2
=(2a+3b)2
(2)原式=
-(x2-4xy+
4y2 )=
-x2-
2 x 2y+
(2y)2
=-(x-2y)2
(3)原式=
3a(x2+2xy
+y2)
=3a(x+y)2
2.下面因式分解对吗？为什么？
1．分解因式：
例2 分解因式:
把2x＋y看做
a2－2ab＋b2
中的字母“a”
即设a＝ 2x＋y ，
这种数学思想称
为换元思想
＝(2x＋y)2－2· (2x＋y) ·3 ＋32
解:
1、用简便方法计算
（1）49.92＋9.98 ＋0.12
（2）9 9992 ＋19 999
2、因式分解
（1）(4a2＋1)2－16a2
（2）(a 2－2)2－4 (a2－2)＋4
（1）形如________________形式的两次三项式可以用完全平方公式分解因式。
（3）因式分解要_________
（2）因式分解通常先考虑______________方法。再考虑 _____________ 方法。
提取公因式法
公式法
彻底
因式分解顺口流
若要分解多项式，先看有无公因式；
看到两次两项式，就用平方差公式；
遇到两次三项式，应用完全平方式；
结果都是积整式，彻底分解多项式。
1、作业本6.3
2、课内作业
作业：
1.用简便方法计算：
绝对挑战
绝对挑战
3. 将　　　　再加上一项，使它成为
完全平方式，你有几种方法？
4.一天,小明在纸上写了一个算式为 4x2 +8x+11,并对小刚说:“无论x取何值,这个代数式的值都是正值,你不信试一试 ”
（1）（ a2+b2)( a2+b2 –10）+25=0 求a2+b2
（2）4x2+y2-4xy-12x+6y+9=0 求x、y关系
（3）分解因式：m4+4
选做题
温馨提示：把a2+b2看做一个整体，可利用换元法.
温馨提示：配方法
温馨提示：添项成完全平方式
能力挑战： 1. 用简便方法计算.
3. 若 ，
则 .
2. 若 是一个完全平方式，
则k = .
观察下表，你还能继续往下写吗？
…
…
7
5
3
1
你发现了什么规律？能用因式分解来说明你发现的规律吗？
任何一个正奇数都可以表示成两个相邻自然数的平方差。对于正奇数2n+1(n为自然数)，有