5.4乘法公式(2)
图片预览







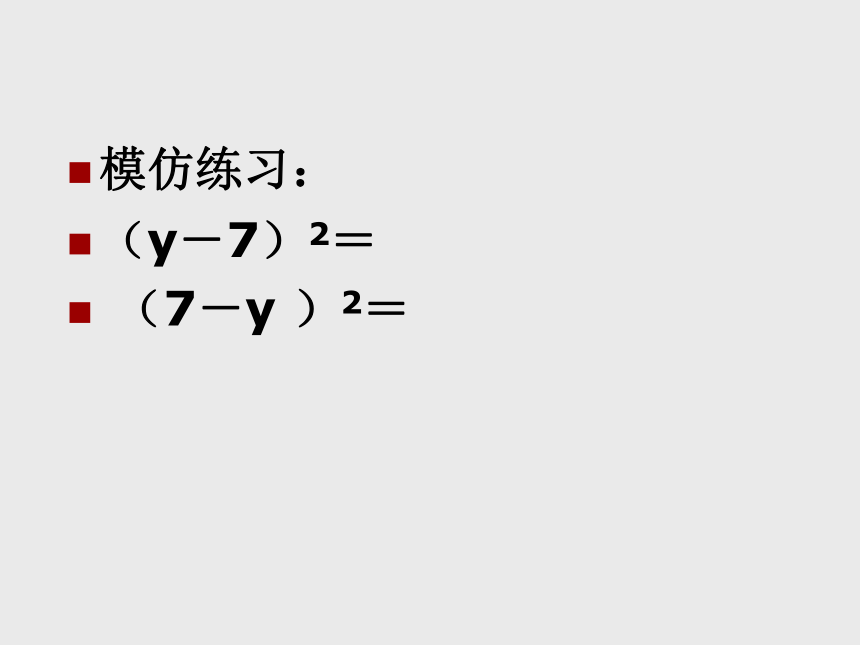
文档简介
(共32张PPT)
平方差公式
练习:用平方差公式计算:
(1)(-3x+4y2)(-4y2-3x)
(2)(x-2)(x2+4)(x+2)(x4+16)
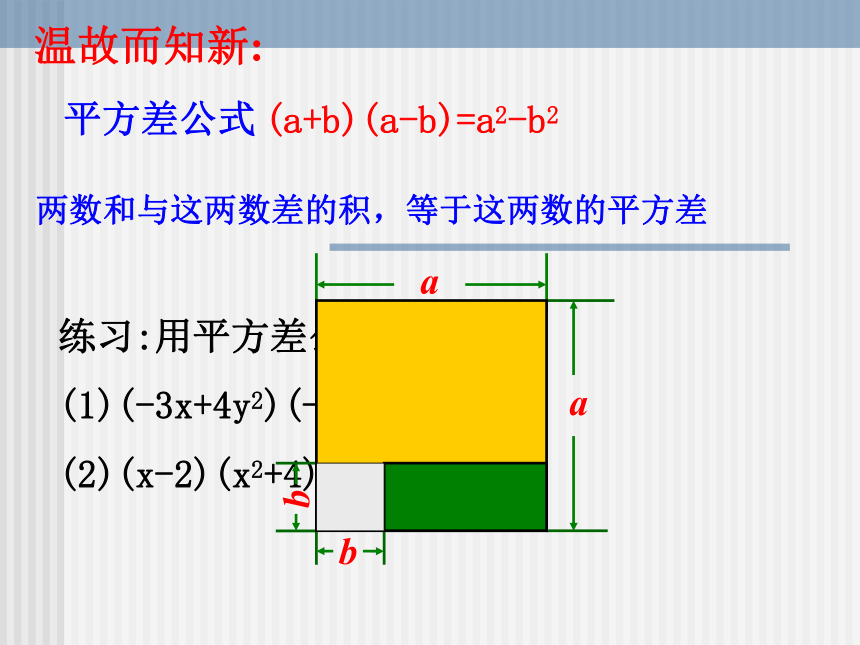
(a+b)(a-b)=a2-b2
温故而知新:
两数和与这两数差的积,等于这两数的平方差
b
a
a
b
1).(3+4)2= 32+42 =
2). (2+6)2= 22+62 =
49
25
64
40
(3+4)2 ≠ 32+42
(2+6)2 ≠ 22+62
运用多项式与多项式相乘的法则计算下列各式:
1、(a+b)2
3、(2a+x)2
观察上述1、2两题的计算结果,你发现有什么规律?你能用你的发现来猜测第3题的结果吗?
合 作 学 习
=(a+b)(a+b)
2、(2+x)2
=(2+x)(2+x)
= 22+2x+2x+x2
=(2a)2+2×2a x+x2
=a2+ab+ab+b2
=a2+2ab+b2
=22+2×2x+x2
b
b
a
a
(a+b)
a
b
ab
ab
+
+
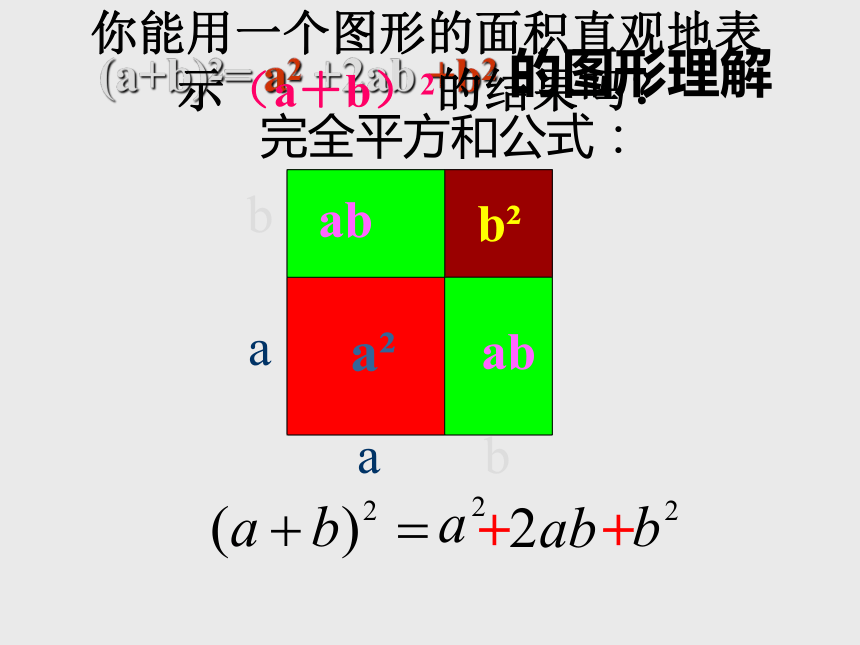
完全平方和公式:
(a+b)2= a2 +2ab +b2 的图形理解
你能用一个图形的面积直观地表示(a+b)2的结果吗?
完全平方公式:
两数和的平方,等于这两数的
平方和 , 加上这两数积的2倍.
(a+b)2=a2+2ab+b2
一般的,我们有以下两数和的完全平方公式:
小明写出了如下的算式:
(a b)2=
[a+( b)]2
他是怎么想的
你能继续做下去吗
a2 2ab+b2.
(a b)2=
(a b)2=
[a+( b)]2
= a2 +2a(-b)+ ( b)2
= a2 –2ab+ b2
a
a
b
b
(a-b)
a
ab
ab
b
b
b
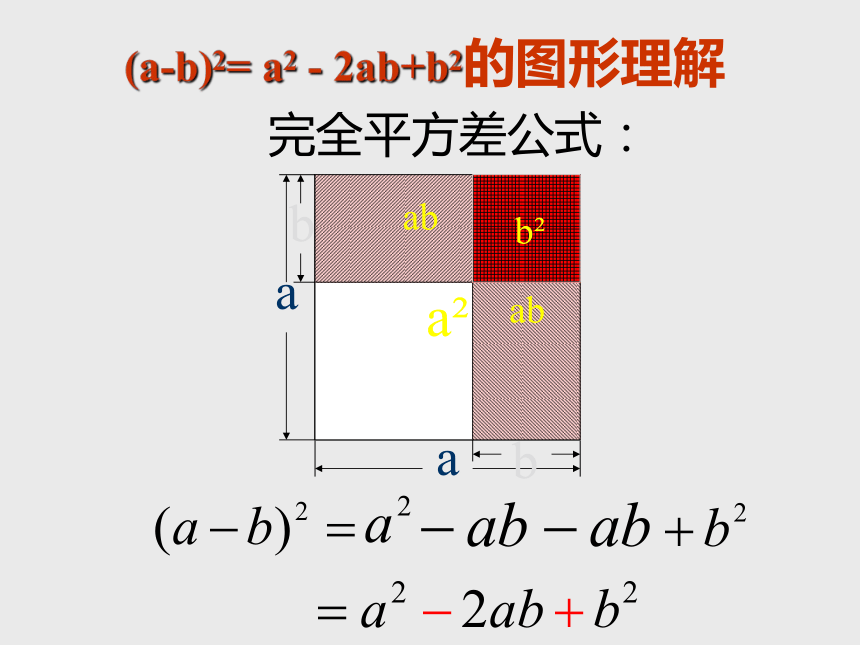
完全平方差公式:
(a-b)2= a2 - 2ab+b2的图形理解
完全平方公式:
两数差的平方,等于这两数的平方和,减去这两数积的2倍.
(a b)2=a2 2ab+b2
模仿练习:
(y-7)2=
(7-y )2=
(a+b)2=a2+2ab+b2
(a b)2=a2 2ab+b2
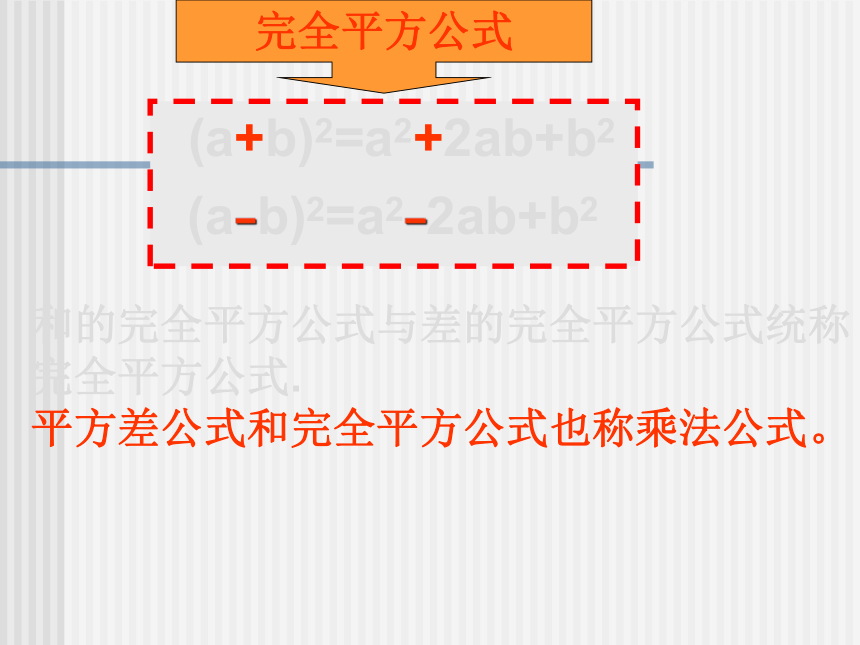
完全平方公式
和的完全平方公式与差的完全平方公式统称完全平方公式.
平方差公式和完全平方公式也称乘法公式。
(a+b)2=a2+2ab+b2
(a b)2=a2 2ab+b2
完全平方公式
结构特征:
左边是:
的平方;
右边是:
(两数和 )
两数的平方和
加上
(减去)
这两数乘积的两倍.
:二项式
(差)
语言表述:
两数和 的平方等于
这两数的平方和
加上 这两数乘积的两倍.
(减去)
或(差)
首平方,尾平方,首尾两倍放中央
公式变形为
(首±尾)2=首2±2×首×尾+尾2
例1 运用完全平方公式计算:
(1)(x+2y)2; (2)(2a-5)2;
(3) (-2s+t)2; (4) (-3x-4y)2.
解:(1)原式=x2+2×x×2y+(2y)2
=x2+4xy+4y2
(2)原式=(2a)2-2×2a×5+52=4a2-20a+25
(3)原式=(-2s)2+2(-2s)t+t2=4s2-4st+t2
(4)原式=(-3x)2-2(-3x)4y+(4y)2
=9x2+24xy+16y2
(2)(-2a2+b)2
例2、运用完全平方公式计算:
(1)( 4a2 - b2 )2
(3)(2a-3b)2-2a(a-b)
1、下面各式的计算是否正确?如果不正确,应当怎样改正?
(2)(x -y)2 =x2 -y2
(3) (x -y)2 =x2-2xy -y2
(4) (x+2y)2 =x2 +2xy +2y2
错
错
错
错
(x +y)2 =x2+2xy +y2
(x -y)2 =x2 -2xy +y2
(x -y)2 =x2 -2xy +y2
(x +2y)2 =x2+4xy +4y2
(1)(x+y)2=x2 +y2
(2) (a - b)2 与 (b - a)2
(1) (-a -b)2 与(a+b)2
2、比较下列各式之间的关系:
相等
相等
(3)(-b +a)2 与(-a +b)2
相等
互为相反数的两式的完全平方结果一样。
3. 下列等式是否成立 说明理由.
(1) ( 4a+1)2=(1 4a)2;
(2) ( 4a 1)2=(4a+1)2;
(3) (4a 1)(1 4a)=(4a 1)(4a 1)
=(4a 1)2;
(4) (4a 1)( 1 4a)=(4a 1)(4a+1).
√
√
×
×
4.在横线上填入适当的整式:
14x
12x
1
例3:一花农有1块正方形茶花苗圃,边长为a(m)。现将这块苗圃的边长都增加1.5m,求这块苗圃的面积增加了多少m 。
a
a
1.5
1.5
(a+1.5) -a
=a +3a+2.25-a
= 3a+2.25
一花农有4块正方
形茶花苗圃,边长分别
为 30.1 m , 29.5 m, 30m,
27m. 现将这4块苗圃的
边长都增加1.5m后,求各苗圃的面
积分别增加了多少m2
生活在线:
解:设原正方形苗圃的边长为a (m),边长增加1.5m后,新正方形的边长为(a+1.5) m。
(a+1.5)2-a2=a2+3a+2.25-a2=3a+2.25
当a=30.1时,3a+2.25=3×30.1+2.25=92.55
当a=29.5时,3a+2.25=3×29.5+2.25=90.75
当a=30 时,3a+2.25=3×30 +2.25=92.25
当a=27 时,3a+2.25=3×27 +2.25=83.25
答:4块茶花苗圃的面积分别增加了92.55m2,90.75m2,92.25m2,83.25m2。
例3、花农老万有4块正方形菜花苗圃,边长分别为30.1m,29.5m,30m,27m。现将这4块苗圃的边长都增加1.5m, 求各苗圃的面积分别增加多少m2?
例:利用完全平方公式计算:
(1) 0.982 (2) 10012
解:(1) 原式 = ( 1 0.02)2
= 12 2 ×1×0.02 + 0.022
= 1 0.04 + 0.0004
= 0.9604
(2)原式 = ( 1000 + 1 )2
= 10002 + 2 × 1000×1 + 12
= 1000000 + 2000 + 1
=1002001
完全平方公式
口诀:首平方,尾平方,首尾两倍放中央
完全平方公式:
1).不漏中间项。2).注意中间项的符号对应。
3).乘方时应适当添括号
注意完全平方公式和平方差公式不同:
形式不同:平方差公式是两数和与两数差的积
完全平方公式的两数和的平方
结果不同:
完全平方公式的结果 是三项,
即 (a b)2=a2 2ab+b2;
平方差公式的结果 是两项,
即 (a+b)(a b)=a2 b2.
(1)化简: (2m+1)2 - (2m)2
(3)用简便的方法计算: 23452+0.76552+2.469×0.7655
做一做:
(4)如果x2+ax+36是一个完全平方式,那么a=______
(6)已知(a+b)2=11,ab=1,求(a-b)2的值.
做一做:
(5)如果x2+6x+b2是一个完全平方式,那么b= ;
±12
±3
1、计算:
2、若 ,则 = 。
提高拓展:
生活在线:要给一边长为a米的正方形桌子辅上正方形的桌布,桌布的四周均超出桌面0.1米,问需要多大面积的桌布.
解:由题意知,桌布是边长为(a+0.2)米的正方形,故面积为:
(a+0.2 )2 = a2 +0.4a+0.04(平方米)
答:所需桌布的面积为a2 +0.4a+0.04(平方米)
着手点:1.桌布的形状
2.边长多少
生活在线:小红用5块工艺布料制作靠垫面子,如图甲,其中四周的4块由如图乙的长方形布料裁成4块得到,正中的一块从另一块布料裁得.正中一块正方形布料应裁取多大的面积(接缝忽略不计)
分析:中间面积
=总面积-周围面积
解:由图得,大正方形的边长为 ,
答:中间正方形的面积应取
平方差公式
练习:用平方差公式计算:
(1)(-3x+4y2)(-4y2-3x)
(2)(x-2)(x2+4)(x+2)(x4+16)
(a+b)(a-b)=a2-b2
温故而知新:
两数和与这两数差的积,等于这两数的平方差
b
a
a
b
1).(3+4)2= 32+42 =
2). (2+6)2= 22+62 =
49
25
64
40
(3+4)2 ≠ 32+42
(2+6)2 ≠ 22+62
运用多项式与多项式相乘的法则计算下列各式:
1、(a+b)2
3、(2a+x)2
观察上述1、2两题的计算结果,你发现有什么规律?你能用你的发现来猜测第3题的结果吗?
合 作 学 习
=(a+b)(a+b)
2、(2+x)2
=(2+x)(2+x)
= 22+2x+2x+x2
=(2a)2+2×2a x+x2
=a2+ab+ab+b2
=a2+2ab+b2
=22+2×2x+x2
b
b
a
a
(a+b)
a
b
ab
ab
+
+
完全平方和公式:
(a+b)2= a2 +2ab +b2 的图形理解
你能用一个图形的面积直观地表示(a+b)2的结果吗?
完全平方公式:
两数和的平方,等于这两数的
平方和 , 加上这两数积的2倍.
(a+b)2=a2+2ab+b2
一般的,我们有以下两数和的完全平方公式:
小明写出了如下的算式:
(a b)2=
[a+( b)]2
他是怎么想的
你能继续做下去吗
a2 2ab+b2.
(a b)2=
(a b)2=
[a+( b)]2
= a2 +2a(-b)+ ( b)2
= a2 –2ab+ b2
a
a
b
b
(a-b)
a
ab
ab
b
b
b
完全平方差公式:
(a-b)2= a2 - 2ab+b2的图形理解
完全平方公式:
两数差的平方,等于这两数的平方和,减去这两数积的2倍.
(a b)2=a2 2ab+b2
模仿练习:
(y-7)2=
(7-y )2=
(a+b)2=a2+2ab+b2
(a b)2=a2 2ab+b2
完全平方公式
和的完全平方公式与差的完全平方公式统称完全平方公式.
平方差公式和完全平方公式也称乘法公式。
(a+b)2=a2+2ab+b2
(a b)2=a2 2ab+b2
完全平方公式
结构特征:
左边是:
的平方;
右边是:
(两数和 )
两数的平方和
加上
(减去)
这两数乘积的两倍.
:二项式
(差)
语言表述:
两数和 的平方等于
这两数的平方和
加上 这两数乘积的两倍.
(减去)
或(差)
首平方,尾平方,首尾两倍放中央
公式变形为
(首±尾)2=首2±2×首×尾+尾2
例1 运用完全平方公式计算:
(1)(x+2y)2; (2)(2a-5)2;
(3) (-2s+t)2; (4) (-3x-4y)2.
解:(1)原式=x2+2×x×2y+(2y)2
=x2+4xy+4y2
(2)原式=(2a)2-2×2a×5+52=4a2-20a+25
(3)原式=(-2s)2+2(-2s)t+t2=4s2-4st+t2
(4)原式=(-3x)2-2(-3x)4y+(4y)2
=9x2+24xy+16y2
(2)(-2a2+b)2
例2、运用完全平方公式计算:
(1)( 4a2 - b2 )2
(3)(2a-3b)2-2a(a-b)
1、下面各式的计算是否正确?如果不正确,应当怎样改正?
(2)(x -y)2 =x2 -y2
(3) (x -y)2 =x2-2xy -y2
(4) (x+2y)2 =x2 +2xy +2y2
错
错
错
错
(x +y)2 =x2+2xy +y2
(x -y)2 =x2 -2xy +y2
(x -y)2 =x2 -2xy +y2
(x +2y)2 =x2+4xy +4y2
(1)(x+y)2=x2 +y2
(2) (a - b)2 与 (b - a)2
(1) (-a -b)2 与(a+b)2
2、比较下列各式之间的关系:
相等
相等
(3)(-b +a)2 与(-a +b)2
相等
互为相反数的两式的完全平方结果一样。
3. 下列等式是否成立 说明理由.
(1) ( 4a+1)2=(1 4a)2;
(2) ( 4a 1)2=(4a+1)2;
(3) (4a 1)(1 4a)=(4a 1)(4a 1)
=(4a 1)2;
(4) (4a 1)( 1 4a)=(4a 1)(4a+1).
√
√
×
×
4.在横线上填入适当的整式:
14x
12x
1
例3:一花农有1块正方形茶花苗圃,边长为a(m)。现将这块苗圃的边长都增加1.5m,求这块苗圃的面积增加了多少m 。
a
a
1.5
1.5
(a+1.5) -a
=a +3a+2.25-a
= 3a+2.25
一花农有4块正方
形茶花苗圃,边长分别
为 30.1 m , 29.5 m, 30m,
27m. 现将这4块苗圃的
边长都增加1.5m后,求各苗圃的面
积分别增加了多少m2
生活在线:
解:设原正方形苗圃的边长为a (m),边长增加1.5m后,新正方形的边长为(a+1.5) m。
(a+1.5)2-a2=a2+3a+2.25-a2=3a+2.25
当a=30.1时,3a+2.25=3×30.1+2.25=92.55
当a=29.5时,3a+2.25=3×29.5+2.25=90.75
当a=30 时,3a+2.25=3×30 +2.25=92.25
当a=27 时,3a+2.25=3×27 +2.25=83.25
答:4块茶花苗圃的面积分别增加了92.55m2,90.75m2,92.25m2,83.25m2。
例3、花农老万有4块正方形菜花苗圃,边长分别为30.1m,29.5m,30m,27m。现将这4块苗圃的边长都增加1.5m, 求各苗圃的面积分别增加多少m2?
例:利用完全平方公式计算:
(1) 0.982 (2) 10012
解:(1) 原式 = ( 1 0.02)2
= 12 2 ×1×0.02 + 0.022
= 1 0.04 + 0.0004
= 0.9604
(2)原式 = ( 1000 + 1 )2
= 10002 + 2 × 1000×1 + 12
= 1000000 + 2000 + 1
=1002001
完全平方公式
口诀:首平方,尾平方,首尾两倍放中央
完全平方公式:
1).不漏中间项。2).注意中间项的符号对应。
3).乘方时应适当添括号
注意完全平方公式和平方差公式不同:
形式不同:平方差公式是两数和与两数差的积
完全平方公式的两数和的平方
结果不同:
完全平方公式的结果 是三项,
即 (a b)2=a2 2ab+b2;
平方差公式的结果 是两项,
即 (a+b)(a b)=a2 b2.
(1)化简: (2m+1)2 - (2m)2
(3)用简便的方法计算: 23452+0.76552+2.469×0.7655
做一做:
(4)如果x2+ax+36是一个完全平方式,那么a=______
(6)已知(a+b)2=11,ab=1,求(a-b)2的值.
做一做:
(5)如果x2+6x+b2是一个完全平方式,那么b= ;
±12
±3
1、计算:
2、若 ,则 = 。
提高拓展:
生活在线:要给一边长为a米的正方形桌子辅上正方形的桌布,桌布的四周均超出桌面0.1米,问需要多大面积的桌布.
解:由题意知,桌布是边长为(a+0.2)米的正方形,故面积为:
(a+0.2 )2 = a2 +0.4a+0.04(平方米)
答:所需桌布的面积为a2 +0.4a+0.04(平方米)
着手点:1.桌布的形状
2.边长多少
生活在线:小红用5块工艺布料制作靠垫面子,如图甲,其中四周的4块由如图乙的长方形布料裁成4块得到,正中的一块从另一块布料裁得.正中一块正方形布料应裁取多大的面积(接缝忽略不计)
分析:中间面积
=总面积-周围面积
解:由图得,大正方形的边长为 ,
答:中间正方形的面积应取
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
