十字相乘法

(共18张PPT)
和差 积
分解因式
整式乘法
你学过哪些分解因式的方法？
提公因式法、
运用公式法。
观察和思考
（1）x2+3x+2是几次几项式？二次项系数、 一次项系数、常数项分别是多少？
（2）它有公因式吗？能用平方差公式，完全平方公式分解因式吗
（3）你觉得该怎样分解？
计算
(1) （x＋2)(x＋1)
(2) (x+2)(x-1)
(3) (x-2)(x-1)
(4) (x+2)(x+3)
(x+p)(x+q)
x2+(p+q)x+pq
一般地,
=x2+3x+2
=X2+x-2
=x2+5x+6
=x2-3x+2
=x2+(p+q)x+pq
= (x+p)(x+q)
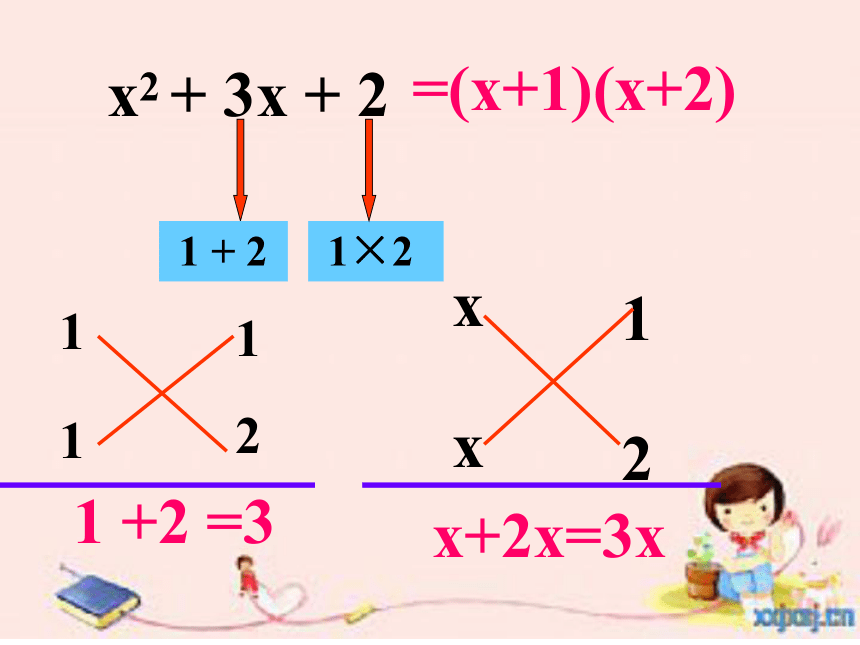
x2 + 3x + 2
1 + 2
1×2
1
1
1
2
1 +2 =3
x
x
1
2
x+2x=3x
=(x+1)(x+2)
十字相乘法：
对于二次三项式的分解因式，借用一个十字叉帮助我们分解因式，这种方法叫做十字相乘法。
即：x2 ＋(p＋q)x＋pq=(x＋p)(x＋q)
x
x
p
q
px＋qx=(p＋q)x
x2
pq
例1 分解因式 x －6x＋8
2
解：x －6x＋8
2
=(x－2)(x－4)
练习一：分解因式
(1) x2-2x-15
(2) －y2 －4y＋12
=(x-5)(x+3)
= - (y+6)(y-2)
-4x-2x=-6x
X
x
-2
-4
对于二次项系数为1的二次三项式分解的方法是“拆常数项，凑一次项”
例2 分解因式 3x －10x＋3
2
解：3x －10x＋3
2
x
3x
－3
－1
－9x－x=－10x
=(x－3)(3x－1)
例3 分解因式 5x －17x－12
2
解：5x －17x－12
2
5x
x
＋3
－4
－20x＋3x=－17x
=(5x＋3)(x－4)
练习二
分解下列因式：
(1)2x2-5x-3
(2)3x2+8xy-3y2
小结：
对于二次项系数不是1的二次三项式分解的方法是“拆两头，凑中间”
=（2x+1)(x-3)
=(3x-y)(x+3y)
先讨论交流，后分解因式。
10(x ＋2)2 －29(x＋2) ＋10
答案 (2x－1)(5x＋8)
7(x+y)3+5(x+y)2-2(x+y)
=(x+y)(x+y+1)(7x+7y-2)
思 考
不解方程组 求3x2+12xy+9y2的值
总结
十字相乘法分解因式的步骤：
1 竖分二次项与常数项。
2 交叉相乘并相加。
3 检验确定，横写因式。
本节课你有什么收获？
口诀：竖分常数交叉验，
横写因式不能乱。
分解因式：
（1）x2y2-xy-2
(2) a2-3a+2
(3) x2+3xy-28y2
(4) 3x2+8x-3